2.2. Правило умножения (произведения)

Формулировка правила умножения (произведения)  применительно к комбинациям из двух объектов: если некоторый объект a можно выбрать M способами и если после каждого такого выбора объект  b можно выбрать N способами, то выбор пары (a,b) в указанном порядке можно осуществить M∙N способами.

Если множества различных вариантов объектов a и b обозначить соответственно через A и B, то каждой паре объектов будет соответствовать один элемент (вектор, кортеж) декартова произведения этих множеств и, как следствие, искомое число | C | комбинаций из двух объектов будет удовлетворять равенству

. (2.5)

Обоснование (интерпретация)  правила. Так как в соответствии с формулировкой при составлении различных комбинаций из двух объектов (указанных пар объектов) число способов выбора второго объекта не зависит от того, как именно выбран первый объект, то все множество комбинаций можно наглядно представить в виде прямоугольной матрицы

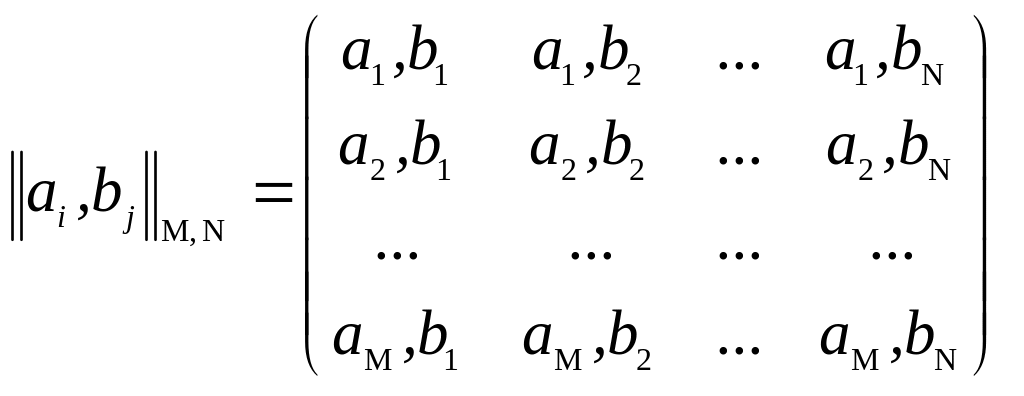
с элементами – кортежами (ai, bj), компоненты которых ai, bj означают i-й вариант (способ выбора) объекта  a  и j-й вариант (способ выбора) объекта  b соответственно. Все множество кортежей, содержащихся в матрице, есть не что иное, как декартово произведение множеств

,

а число кортежей (пар объектов), совпадающее с мощностью | C | декартова произведения, очевидно, равно , что подтверждает справедливость правила умножения и равенства (2.5).

Сформулированные правила сложения и умножения при решении комбинаторных задач редко применяются по отдельности, обычно они дополняют друг друга (см. пример 2.3). Для примера 2.3 (как и для примера 2.1) характерно то, что для решения сформулированной в нем задачи можно использовать (и используется) два приема: первый сводится к реализации полученных рекуррентных соотношений, а второй – к заполнению прямоугольной матрицы (таблицы). В следующей главе будет рассмотрен еще один пример, предполагающий применение готовых формул. К сожалению, использование альтернативных приемов, а тем более готовых формул (аналитических выражений) возможно далеко не всегда. Встречаются ситуации, когда кроме общих правил ничего не применишь. Одна из таких ситуаций рассмотрена в примере 2.4.

Обобщение правила  умножения (произведения) для комбинаций с произвольным числом объектов: если множество всевозможных комбинаций (кортежей) объектов представляет собой декартово произведение D = , то

. ( 2.6 )

Обоснование справедливости равенства (2.6), отражающего правило нахождения мощности декартова произведения произвольного числа множеств, не представляет большого труда. Это можно сделать, например, с помощью хорошо известного метода математической индукции.

Наиболее часто правило умножения применяется в ситуациях, когда сомножители в декартовом произведении совпадают, т.е. A = B = C =...= G. Для таких ситуаций равенство (2.6) принимает вид

, ( 2.7 )

где n - количество сомножителей (число объектов в комбинации, длина кортежа объектов).

Множество A, определяющее декартову степень, при решении комбинаторных задач довольно часто называют алфавитом, а элементы декартовой степени, т.е. кортежи, составленные из объектов (элементов) множества A (букв алфавита), - словами в этом алфавите. Число n называют длиной слова (см. пример 2.5). Таким образом, применительно к декартовой степени правило умножения и формула (2.7) определяют количество слов длиной n, которые можно составить (записать) с помощью m букв алфавита A ( m = | A | ).