
- •1. Статистическое наблюдение, его формы, виды и способы.
- •2. Виды статистических группировок. Построение группировки по количественному признаку
- •3. Абсолютные, средние и относительные статистические показатели.
- •4 Аналитические показатели временного ряда
- •5. Индивидуальные и сводные индексы, их взаимосвязи.
- •6. Методы проверки временных рядов на наличие тенденции.
- •7. Методы выбора формы трендовой модели
- •8. Построение моделей авторегрессионных преобразований.
- •1. Основан на использовании, так называемых, последовательных или конечных разностей.
- •2. Метод отклонений эмпирических значений признака от теоретических по уравнению тренда полученных.
- •3. Метод Фриша-Воу
- •9. Прогнозирование на основе средних аналитических показателей временных рядов.
- •10. Прогнозирование на основе экстраполяции тренда.
- •11. Прогнозирование с учетом дисконтирования информации
- •12. Прогнозирование на основе кривых роста Гомперца и Перля-Рида.
- •13. Автокорреляция, ее выявление в уровнях временного ряда
- •14. Прогнозирование связных временных рядов
- •15. Оценка точности и надежности прогнозов.
- •16. Основные понятия теории выборочного наблюдения
- •17. Алгоритмы формирования выборочной совокупности
- •18. Простая случайная и систематическая выборки
- •19. Расслоенная выборка
- •20. Кластерная (сериальная) выборка
- •21.Предмет, задачи и система показателей макроэкономической статистики
- •22. Статистическое исследование результатов экономической деятельности
- •23. Статистическое исследование трудового потенциала и трудовых ресурсов
- •24. Статистическое исследование цен и ценообразования
- •25.Статистическое исследование внешней экономической деятельности
- •26. Сводный счет «Производство», его назначение и система показателей.
- •27. Методология исчисления валового внутреннего продукта и национального дохода
- •28. Межотраслевой баланс производства и распределения продукции в снс
- •29. Система макроэкономических показателей, применяемая в международной статистической практике
- •30. Предмет, метод, функции и система показателей социальной статистики
- •1. Общество, его основные характеристики и дифференциация
- •2. Условия жизни
- •3. Уровень жизни (материальная сторона)
- •4. Способ жизни и качественные аспекты жизни
- •Расчет коэффициентов корреляции Кэндела и Спирмена . [-1;1]
- •31.Статистическое исследование социальной структуры и социальной мобильности населения
- •32.Статистическое исследование жизненного уровня населения
- •33.Статистическое исследование дифференциации населения по денежным доходам
- •34.Статистическое исследование сферы обслуживания и охраны здоровья населения
- •35.Предмет, задачи и система показателей демографической статистики
- •36.Статистическое исследование численности, размещения и состава населения
- •37.Статистическое исследование естественного движения населения
- •38.Статистическое исследование миграционного движения населения.
- •39.Статистическое исследование воспроизводства населения
- •40. Понятие, принципы и методы демографического прогнозирования
- •41.Случайные величины. Закон распределение вероятностей дискретной случайной величины
- •42. Функция распределения и плотность вероятности случайной величины, их свойства
- •43. Основные числовые характеристики случайной величины и их свойства
- •44.Биноминальный и нормальный законы распределения случайной величины
- •45.Парные и частные коэффициенты корреляции, их свойства
- •46. Множественные коэффициенты корреляции и детерминации, их свойства
- •47. Понятие генеральной совокупности и выборки из нее
- •48. Определение точечной оценки (статистики) и основные требования, предъявляемые к точечной оценке (несмещенность, состоятельность, эффективность)
- •49. Интервальные оценки параметров генеральной совокупности
- •50. Интервальная оценка генеральной средней нормально распределенной генеральной совокупности.
- •51. Интервальная оценка генеральной дисперсии нормально распределенной генеральной совокупности.
- •52. Статистические гипотезы и правила их проверки. Статистические критерии.
- •53. Сущность дисперсионного анализа. Основные задачи, решаемые с его помощью
- •54. Определение оценок параметров классической линейной модели множественной регрессии с помощью метода наименьших квадратов
- •55. Факторный и компонентный анализ как методы снижения размерности
- •56. Кластерный анализ как метод многомерной классификации
- •57. Проверка значимости уравнения множественной регрессии и его коэффициентов. Интервальное оценивание коэффициентов уравнения регрессии
- •58. Гомо- и гетероскедастичность остатков в регрессионных моделях.
- •59. Обобщенный метод наименьших квадратов (омнк). Свойства омнк-оценок
- •60. Дискриминантный анализ как метод многомерной классификаций с обучением
53. Сущность дисперсионного анализа. Основные задачи, решаемые с его помощью
Дисперсионный анализ (от латинского Dispersio – рассеивание) – статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
Основные понятия дисперсионного анализа
В процессе наблюдения за исследуемым объектом качественные факторы произвольно или заданным образом изменяются. Конкретная реализация фактора (например, определенный температурный режим, выбранное оборудование или материал) называется уровнем фактора или способом обработки. Модель дисперсионного анализа с фиксированными уровнями факторов называют моделью I, модель со случайными факторами - моделью II. Благодаря варьированию фактора можно исследовать его влияние на величину отклика. В настоящее время общая теория дисперсионного анализа разработана для моделей I.
В основе дисперсионного анализа лежит
разделение дисперсии на части или
компоненты. Вариацию, обусловленную
влиянием фактора, положенного в основу
группировки, характеризует межгрупповая
дисперсия σ2. Она является мерой
вариации частных средних по группам
![]() вокруг общей средней
вокруг общей средней
![]() и определяется по формуле:
и определяется по формуле:
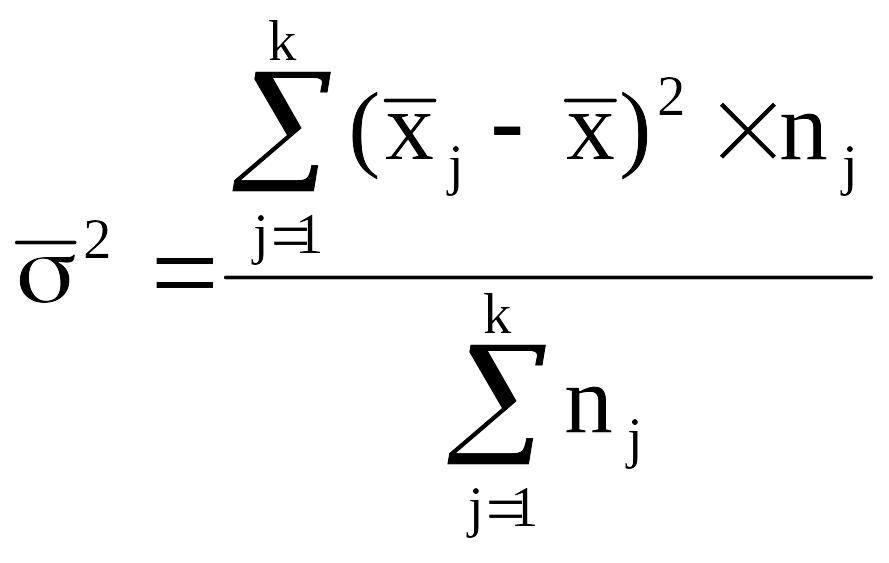 ,
,
где k - число групп;
nj - число единиц в j-ой группе;
![]() -
частная средняя по j-ой
группе;
-
частная средняя по j-ой
группе;
- общая средняя по совокупности единиц.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия σj2.
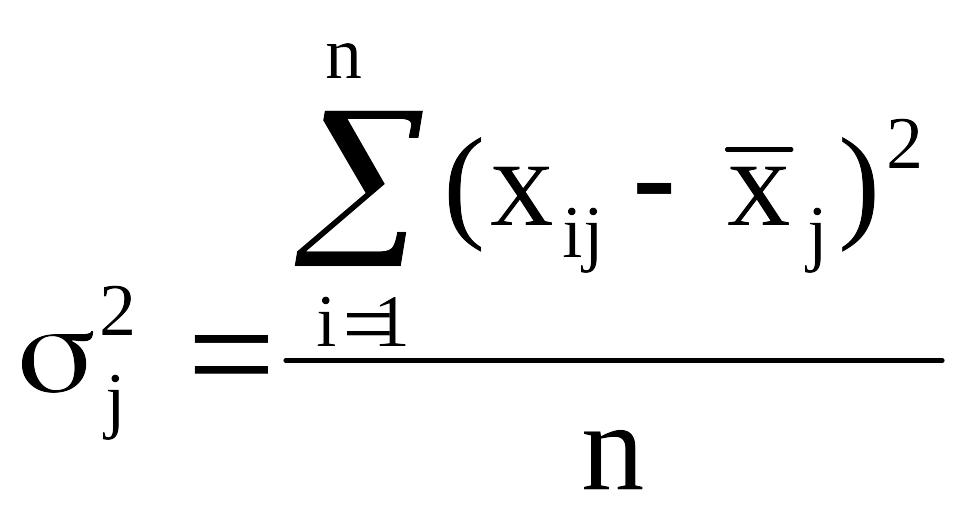 .
.
Между общей дисперсией σ02,
внутригрупповой дисперсией σ2 и
межгрупповой дисперсией
![]() существует
соотношение:
существует
соотношение:
σ02 =
![]() +
σ2.
+
σ2.
Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе.
Однофакторный комплекс
Изучается влияние на нормально
распределенный результативный признак
одного контролируемого фактора
![]() ,
имеющего
,
имеющего
![]() уровней
уровней
![]() .
.
Под уровнем фактора подразумевается его мера или состояние, т.е. некоторое количественное или качественное значение.
Двухфакторный комплекс
Изучается влияние на нормально
распределенный результативный признак
фактора
,
имеющего
уровней
![]() и фактора
и фактора
![]() с
с
![]() уровнями
уровнями
![]() .
.
содержание
54. Определение оценок параметров классической линейной модели множественной регрессии с помощью метода наименьших квадратов
Регрессионный анализ – это статистический метод исследования зависимости случайной величины Y от переменных Xj (j = 1, 2, ..., k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения Xj.
Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид:
y = β0 +β1хi1 +...+βjxij+...+βkxik+εi (2.1)
где εi – случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию σ2
В матричной форме регрессионная модель имеет вид:
Y = Xβ + ε (2.2)
где Y – случайный вектор – столбец размерности (n x 1) наблюдаемых значений результативного признака (y1, y2,..., yn); X – матрица размерности [n x (k+1)] наблюдаемых значений аргументов. Элемент матрицы xij рассматривается как неслучайная величина (i =1,2,...,n; j=0,1,2,...k; x=1); β-вектор – столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели; ε-случайный вектор – столбец размерности (n x 1) ошибок наблюдений (остатков). Компоненты вектора ε независимы между собой, имеют нормальный закон распределения с нулевым математическим ожиданием (Mε=0) и неизвестной дисперсией σ2 (D εi = σ2).
Для оценки вектора β наиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки принимают вектор b, который минимизирует сумму квадратов отклонения наблюдаемых значений yi от модельных значений ŷ, т. е. квадратичную форму:
![]()
Дифференцируя, с учетом квадратичную
форму Q по вектору β:
![]()
![]()
и приравнивая производные нулю, получим
оценку метода наименьших квадратов:
![]()
Получаем вектор оценок b, где b=(b0 b1...bk)T.
Оценка ковариационной матрицы коэффициентов регрессии вектора b определяется из выражения:
![]() , где
, где
![]()
содержание
