4 Аналитические показатели временного ряда
На практике для количественной оценки динамики явлений широко применяется ряд основных аналитических показателей. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. При этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.
Абсолютный прирост (Δ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста. В общем случае абсолютный прирост может быть представлен в виде:
где yi – текущий уровень ряда динамики;
i = 2,3,…,n; k = 1,2,…,n-1.
При k = 1 от текущего уровня yi вычитается
предыдущий уровень yi-1, и получается
формула для расчета цепного
абсолютного прироста:
базисный абсолютный
прирост определяется относительно
начального уровня ряда:
Базисный абсолютный прирост определяется не всегда относительно первого уровня, он также может быть определен относительно уровня ряда динамики, принятого за базу сравнения.
Показатель интенсивности изменения уровня ряда – в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста. Разница между ними заключается только в единице измерения.
Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).
Темпы роста характеризуют отношение двух сравниваемых уровней ряда в виде:
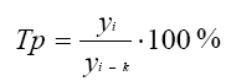где
yi – текущий уровень ряда динамики; i =
2,3,…,n; k = 1,2,…,n-1.
Цепной:
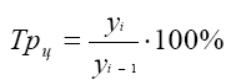Базисный:
где y1 – уровень ряда динамики, принятый за базу сравнения.
Темп прироста характеризует абсолютный прирост в относительных величинах. Определенный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения:
Если темп роста всегда положительное число, то темп прироста может быть положительным, отрицательным и равным нулю. Зависимость цепного темпа прироста от цепного темпа роста:
где
Трц – цепной темп роста.
Базисный темп прироста равен отношению базисного абсолютного прироста к уровню ряда, принятому за базу сравнения:
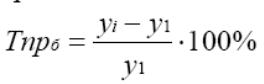
Зависимость базисного темпа прироста от базисного темпа роста:
где
Трб – базисный темп роста.
На практике часто проводят сопоставление показателей абсолютного прироста и темпа прироста за одни и те же периоды времени. Для этого рассчитывают абсолютное значение одного процента прироста. Оно представляет собой одну сотую часть базисного уровня и в то же время – отношение абсолютного прироста к соответствующему темпу прироста:
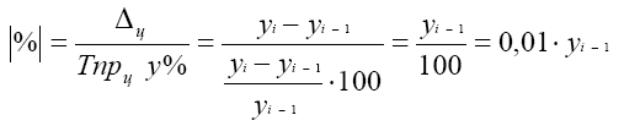
Таким образом, базисные показатели динамики характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i-го) периода. Цепные показатели динамики характеризуют интенсивность изменения уровня от периода к периоду в пределах изучаемого промежутка времени.
содержание