
- •Оглавление
- •Введение
- •Общий вид задачи линейного программирования
- •Решение задачи линейного программирования графическим методом.
- •.Решение задачи линейного программирования симплекс-методом.
- •Симплекс-метод, решение задачи с искусственным базисом
- •Двойственная задача.
- •Задачи для самостоятельного решения
- •Составить математическую модель задачи
- •Решить задачу линейного программирования графическим способом
- •Решить злп симплекс-методом
- •Контрольные вопросы
- •Заключение
- •Литература
Общий вид задачи линейного программирования
Задача оптимального планирования является самой важной из задач линейного программирования. Если сформулировать задачу линейного программирования без экономической интерпретации, то она такова: найти экстремум линейной функции при линейных же ограничениях на переменные. При этом множество значений переменных, удовлетворяющих всем ограничениям задачи, называется допустимым множеством. Допустимое множество представляет собой некоторое многогранное тело в линейном числовом пространстве размерности, равной числу переменных задачи. Линейная же функция, экстремум которой ищется, называется целевой функцией. Задачу линейного программирования можно сформулировать так . Найти max
 при
условии :
при
условии :
a11 x1 + a12 x2 + . . . + a1n xn b1 ;
a21 x1 + a22 x2 + . . . + a2n xn b2 ;
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
am1 x1 + am2 x2 + . . . + amn xn bm ;
x1 0, x2 0, . . . , xn 0 .
Эти ограничения называются условиями неотрицательности. Или в матричном виде
(1)
 (2)
(2)
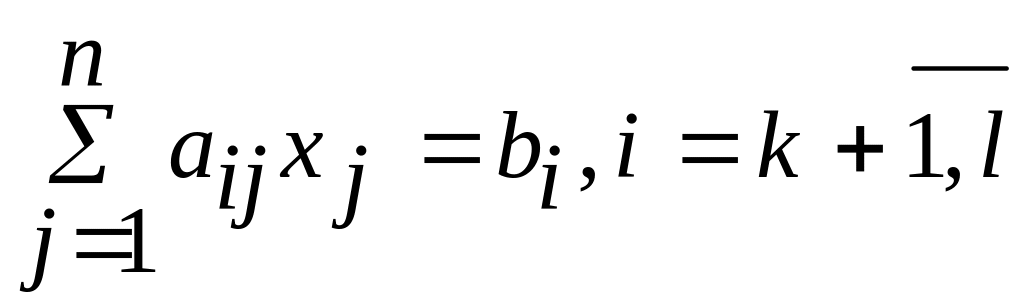 (3)
(3)
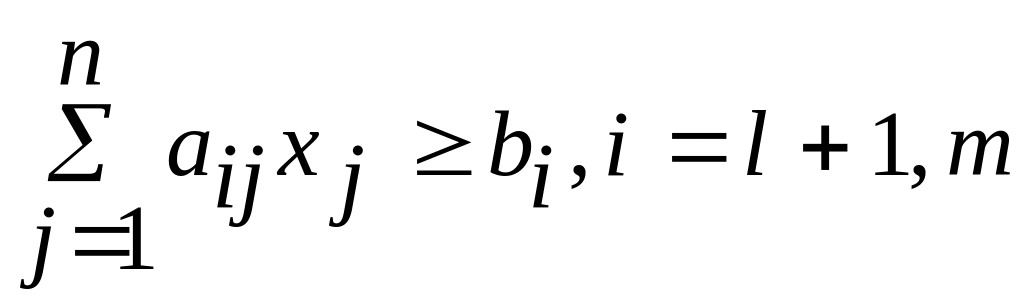 (4)
(4)
![]() ,
,![]() (5)
(5)
При этом система линейных уравнений(3) и неравенств(2),(4),(5), определяющая допустимое множество решений задачи, называется системой ограничений задачи линейного программирования, а линейная функция Z называется целевой функцией или критерием оптимальности. В задачах линейного программирования целевая функция линейна, а условия-ограничения содержат линейные равенства и линейные неравенства. Если все ограничения имеют вид неравенств, то задача записана в стандартной форме. Если все ее ограничения, кроме
![]()
представляют собой равенства, то задача линейного программирования записана в канонической форме. Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме.
Правило приведения задачи линейного программирования к канонической форме состоит в следующем:
1. Правые части всех
ограничений должны быть неотрицательными
![]() .
Если какой-нибудь из коэффициентов
.
Если какой-нибудь из коэффициентов
![]() <
0, то необходимо коэффициенты ограничения
слева и справа домножить на "-1" и
изменить знак данного ограничения на
противоположный;
<
0, то необходимо коэффициенты ограничения
слева и справа домножить на "-1" и
изменить знак данного ограничения на
противоположный;
2. Все ограничения должны быть представлены в виде равенств, поэтому при переходе от неравенства к равенству используют аппарат дополнительных переменных.
Если исходные ограничения
определяют расход некоторого ресурса
(знак "![]() "),
то переменные
"),
то переменные
![]() следует интерпретировать как остаток,
или неиспользованную часть ресурса. В
этом случае
следует интерпретировать как остаток,
или неиспользованную часть ресурса. В
этом случае
![]() –
остаточная переменная и вводится в
уравнение со знаком "+".
–
остаточная переменная и вводится в
уравнение со знаком "+".
Если исходные ограничения
определяют избыток некоторого ресурса
(знак "![]() "),
то вводится избыточная переменная
"),
то вводится избыточная переменная
![]() знаком
"-".
знаком
"-".
3. Все переменные должны
быть неотрицательными, т.е.
![]() .
.
Если переменная не
имеет ограничения в знаке, то её нужно
представить как разность двух
неотрицательных переменных:
![]() ,
где
,
где
![]() .
Такую подстановку следует использовать
во всех ограничениях, содержащих эту
переменную, а также в выражении для
целевой функции.
.
Такую подстановку следует использовать
во всех ограничениях, содержащих эту
переменную, а также в выражении для
целевой функции.
Если такая переменная попадает в оптимальное решение, то
![]() .
.
4. Целевая функция: Подлежит максимизации или минимизации.
Max f(x)= min (-f(x))
Система ограничений в виде равенств и неравенств образует выпуклое множество - выпуклый многогранник. Это множество может быть ограниченным и неограниченным. Целевая функция задачи линейного программирования также является выпуклой функцией. Таким образом, задача линейного программирования является частным случаем задачи выпуклого программирования.
Для решения задач линейного программирования применяются методы:
1) графический;
2) табличный ( прямой, простой ) симплекс - метод;
3) метод искусственного базиса;
4) модифицированный симплекс - метод;
