
Лабораторная работа №5
ОПРЕДЕЛЕНИЕ СP/СV С ИСПОЛЬЗОВАНИЕМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ И ИЗОХОРИЧЕСКОГО НАГРЕВА
Цель работы: Экспериментально определить постоянную адиабаты воздуха методом адиабатического расширения и изохорического нагрева.
Литература:
1. Сивухин Д.В. Общий курс физики. Т.2. Термодинамика и молекулярная физика. – М.: Наука, 1990, гл. II, §§ 21, 22.
2. Кикоин А.К., Кикоин И.К. Молекулярная физика. — М.: Наука, 1976, гл. II, §§ 30.
3. Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. – М.: Наука, 1965, гл. VII, §§ 56, 57.
4. Введение в технику эксперимента/ Составитель: Беленко И.А. – БелГУ, 2004. – 124 с.
Приборы, оборудование и их характеристики:
Стеклянный баллон;
U – образный водяной манометр;
Резиновая груша;
Электронный секундомер «Интеграл ЧС – 01».
Теория метода
Отношение
теплоемкостей газа при постоянном
давлении и при постоянном объеме
![]() играет в термодинамике весьма важную
роль. В частности, оно входит в уравнение
Пуассона, которое описывает адиабатическое
расширение газа (процесс, который
протекает без обмена теплом между
термодинамической системой и окружающей
средой)
играет в термодинамике весьма важную
роль. В частности, оно входит в уравнение
Пуассона, которое описывает адиабатическое
расширение газа (процесс, который
протекает без обмена теплом между
термодинамической системой и окружающей
средой)
![]() =const.
(1)
=const.
(1)
Поскольку идеальной
теплоизоляции не существует, то реальный
процесс не может быть строго адиабатическим.
Но если термодинамический процесс
проходит быстро, то за время протекания
процесса сколько-нибудь значительный
теплообмен произойти не успевает, и
такой процесс можно с достаточной
точностью считать адиабатическим. Этот
прием используется в одном из самых
простых методов определения
![]() – методе
адиабатического расширения и изохорического
нагрева (метод Клемана и Дезорма).
– методе
адиабатического расширения и изохорического
нагрева (метод Клемана и Дезорма).
Пусть в закрытом стеклянном сосуде находится исследуемый газ при комнатной температуре Т1 и давлении p1, несколько превышающем атмосферное давление p0.
Откроем кран, сообщающий сосуд с атмосферой. Давление газа начнет сравниваться с атмосферным, а его температура сначала несколько понизится из-за быстрого расширения, а затем снова начнет приближаться к комнатной.
Если теплопроводность стенок сосуда мала (стекло обладает, как известно, низкой теплопроводностью), а отверстие крана достаточно велико, то равновесие по давлению устанавливается значительно быстрее, чем равновесие по температуре, т.е.
![]() ,
(2)
,
(2)
где через
![]() обозначены соответственно времена
выравнивания давления и температуры.
обозначены соответственно времена
выравнивания давления и температуры.
Пусть кран был
открыт в течение промежутка времени
![]() такого,
что
такого,
что
![]() .
(3)
.
(3)
В этом случае теплообменом, происходящим за время через стенки баллона, можно пренебречь, и процесс расширения оказывается почти адиабатическим.
Заметим, что в конце адиабатического расширения давление р2 равно атмосферному давлению р0, а температура Т2 оказывается несколько ниже комнатной температуры Т1, т. е. Т2 <Т1 (температура газа понижается, так как работа расширения совершается за счет внутренней энергии газа)1.
Переходя в (1) с помощью уравнения Менделеева – Клапейрона к переменным р, Т, найдем, что для адиабатического процесса
 или
или
 .
(4)
.
(4)
После того, как кран вновь отключает сосуд от атмосферы, происходит медленное изохорное нагревание газа со скоростью, определяемой теплопроводностью стеклянных стенок. Вместе с ростом температуры растет и давление газа. За время
![]()
система достигает равновесия, и установившаяся температура газа T становится равной комнатной температуре T1.
Процесс выравнивания температуры при закрытом кране подчиняется закону Гей-Люссака (изохора)
![]() откуда
откуда
![]() .
(5)
.
(5)
Исключая с помощью (5) отношение температур T1/Т2 из (4), найдем
 или
или

Разрешим это
уравнение
относительно
![]() .
Для этого прологарифмируем это равенство.
Получим
.
Для этого прологарифмируем это равенство.
Получим
 ,
откуда
,
откуда
 .
(6)
.
(6)
Таким образом, определение показателя адиабаты по методу Клемана-Дезорма требует последовательного проведения с исследуемым газом двух термодинамических процессов – адиабатического (1-0) и изохорного (0-2) (см. рис.1). Показатель адиабаты определяется тремя давлениями – p1 и p0 до и после адиабатического расширения и давлением p2 после изохорного нагревания системы до первоначальной температуры. При этом измерений температуры не требуется.
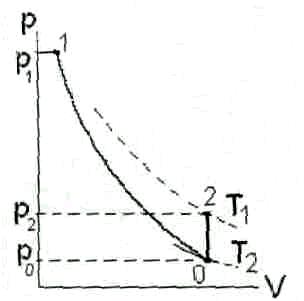
Рис. 1. Метод Клемана-Дезорма: последовательность термодинамических процессов
