3. Если , то система имеет бесконечно много решений.

Пример 4. Решить систему линейных уравнений _.

Решение. Составим определитель из коэффициентов при неизвестных и вычислим его:

, значит, СЛУ имеет единственное решение. Найдем вспомогательные определители и значения неизвестных.

Ответ: .

Рассмотрим пример, в котором СЛУ имеет бесконечное множество решений, и они будут найдены с применением формул Крамера.

Пример 5. Решить СЛУ.

Решение.

Вычислим определитель системы:

Заметим, что третье уравнение системы равно сумме первых двух уравнений, т.е. зависит от первых двух уравнений. Отбросив третье уравнение, получим равносильную систему двух уравнений с тремя неизвестными:

Оставим в левой части системы те неизвестные, коэффициенты при которых образуют определитель, не равный нулю, например, . Неизвестное является свободным, а неизвестные и - базисными неизвестными. Запишем систему в виде и применим к ней правило Крамера:

;

- общее решение неопределенной СЛУ, где - любое действительное число.

Из общего решения можно получить частные решения, если придать свободной неизвестной какое-то конкретное значение. Например, пусть , тогда ; частное решение .

3. Матричный метод решения слу

3.1. Матричная запись системы линейных уравнений

Пусть - матрица коэффициентов при неизвестных, - матрица-столбец неизвестных, - матрица-столбец свободных членов. Система уравнений с неизвестными в матричном виде запишется как (матричное уравнение системы):

.

3.2. Решение системы уравнений с помощью обратной матрицы

Умножив обе части уравнения системы на обратную матрицу слева и используя свойство , получим выражение для матрицы неизвестных . Оно показывает, как найти решение системы линейных уравнений с неизвестными с помощью обратной матрицы.

Пример 6. Решить с помощью обратной матрицы систему уравнений

.

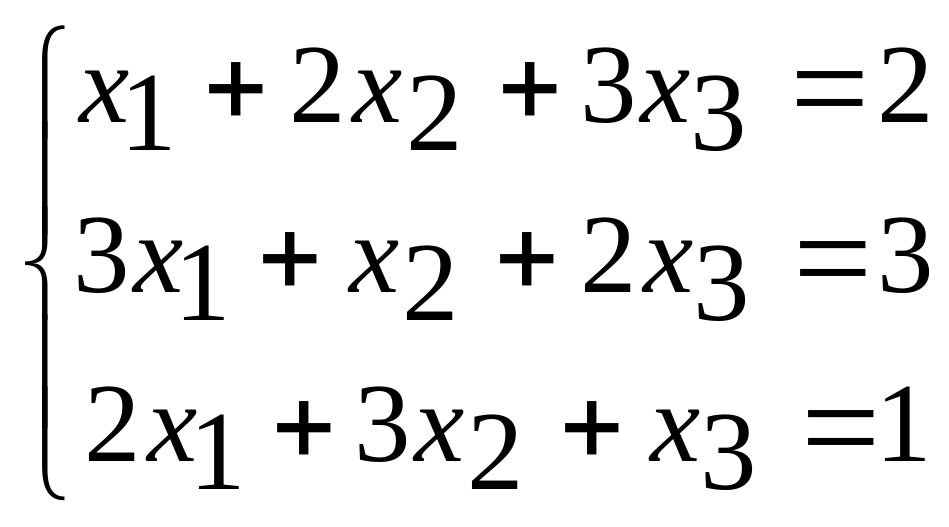Решение. Вычислим определитель: . Так как , то система уравнений имеет единственное решение .

2) Составим обратную матрицу. Матрица существует, т.к. определитель . Найдем алгебраические дополнения .

, , ,

, , ,

, , .

Составим матрицу из алгебраических дополнений и транспонируем ее. .

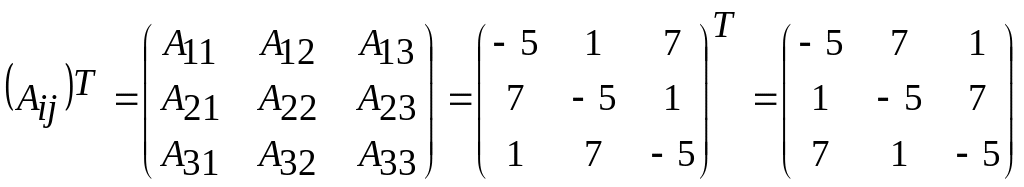Разделим каждый элемент этой матрицы на определитель , получим искомую обратную матрицу: .

3) Матрица неизвестных равна произведению матрицы на матрицу свободных членов :

.

Вычислим значения неизвестных: , , .

Ответ. Система имеет единственное решение .

4. Сущность метода исключения неизвестных (метода Гаусса). Элементарные преобразования

Сущность метода Гаусса состоит в том, что система линейных уравнений с помощью элементарных преобразований приводится к равносильной системе треугольного или трапецеидального вида, из которой легко находится решение системы или делается вывод о несовместности системы. Метод Гаусса применяется к любой СЛУ, в которой число уравнений равно числу неизвестных, или больше числа неизвестных, или меньше числа неизвестных.

К элементарным преобразованиям над уравнениями системы относятся:

1. Перестановка уравнений местами.

2. Умножение уравнения на число, не равное нулю.

3. Прибавление одного уравнения к другому уравнению, умноженному на какое-либо число.

4. Отбрасывание одинаковых уравнений (кроме одного), а также уравнения вида .