1.3. Начальная остойчивость

При наклонении судна внешними силами линии действия сил тяжести и поддержания не совпадают, а, оставаясь параллельными, создают пару, момент которой препятствует наклонению (см.рис.1.10.а). При статических наклонениях значение этого восстанавливающего момента является мерой остойчивости судна, а при динамическом приложении внешних сил способность судна противостоять наклонениям оценивается работой восстанавливающего момента.

Восстанавливающие моменты M_B и их работа A_B определяются по структурным формулам:

, (1.6)

где - угол наклонения (в любой плоскости); - плечо восстанавливающего момента.

Любое наклонение судна с достаточной точностью можно представить в виде комбинации крена и дифферента, а возникающий при этом восстанавливающий момент - геометрической суммой восстанавливающего момента при крене M_B( ) и восстанавливающего момента при дифференте M_B ( ).

При малых поперечных наклонениях плечо восстанавливающего момента определяется выражением , где начальная поперечная метацентрическая высота (НПМВ) h₀=r+z_c-z_g (рис.1.10.б), а восстанавливающий момент при крене . При продольных наклонениях восстанавливающий момент , а продольная метацентрическая высота H₀=R+z_c-z_g (см.рис.1.10.в).

Метацентрические радиусы r=J_x/V и R=J_f/V, где J_x и J_f - центральные моменты инерции площади действующей ВЛ.

Значения V, J_x, J_f ,z_c, r и R рассчитываются по теоретическому чертежу, и, как функции от осадки, приводятся на кривых плавучести и начальной остойчивости (рис.1.11).

Выражения, определяющие восстанавливающие моменты при малых наклонениях, называются метацентрическими формулами остойчивости и пригодны для решения эксплуатационных задач, связанных с определением посадки судна, когда результаты расчета не направлены на оценку безопасности плавания. При этом применяются следующие расчетные формулы:

h₀=r+z_c-z_g; H₀=R+z_c-z_g; r=J_x/V; R=J_f/V, (1.7)

где k=Dh₀, K=DH₀ -- коэффициенты поперечной и продольной остойчивости.

Момент, кренящий судно на 1⁰ M₀=Dh₀/57,3. Момент, дифферентующий судно на 1 см .

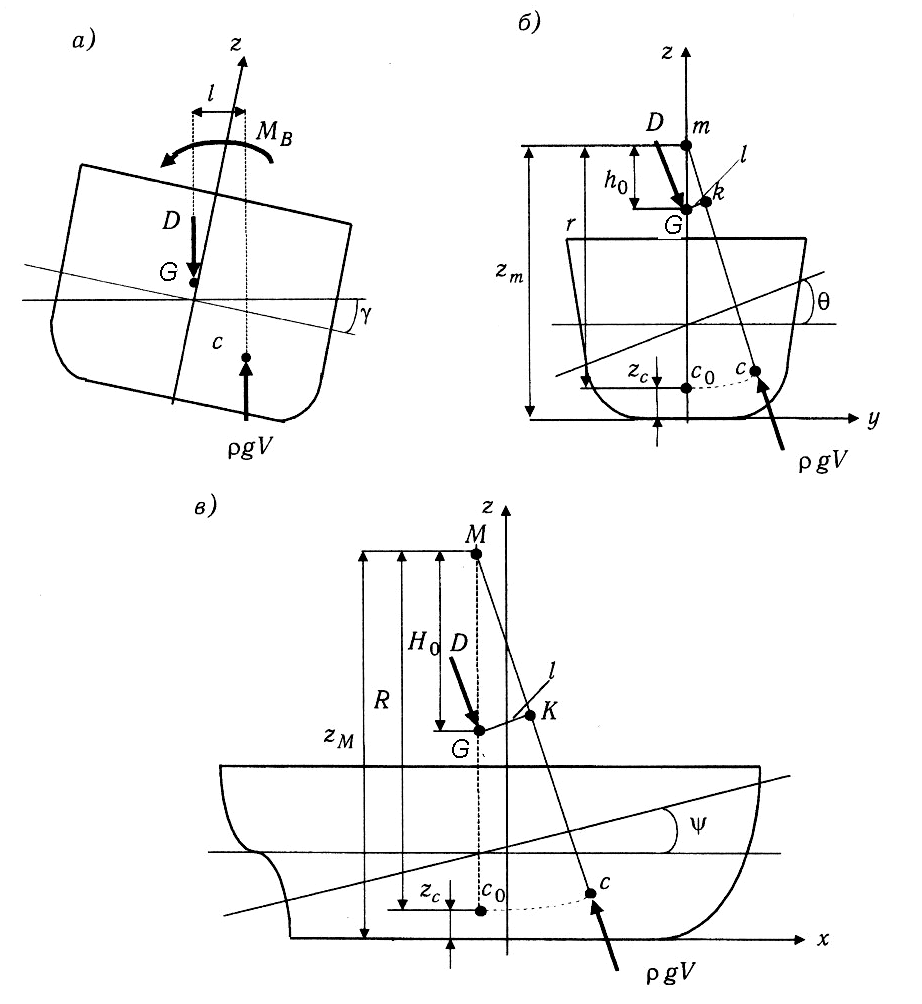
Рис.1.10. a) Пары сил и восстанавливающий момент; метацентрические радиусы и метацентрические высоты при крене (б) и дифференте (в)

При отсутствии кривых элементов Т.Ч. величины, входящие в (1.7), могут быть определены по приближенным формулам:

. (1.8)

При перемещениях грузов в горизонтальной плоскости, вызывающих малые наклонения, остойчивость судна, т.е. способность противостоять наклонениям, остается неизменной. При перемещении грузов по вертикали изменяется аппликата Ц.Т. судна -- z_g и, следовательно, метацентрические высоты и коэффициенты остойчивости. Эти изменения определяются выражениями:

,

где m - масса перемещенного груза; (z₂-z₁) - плечо переноса груза по вертикали.

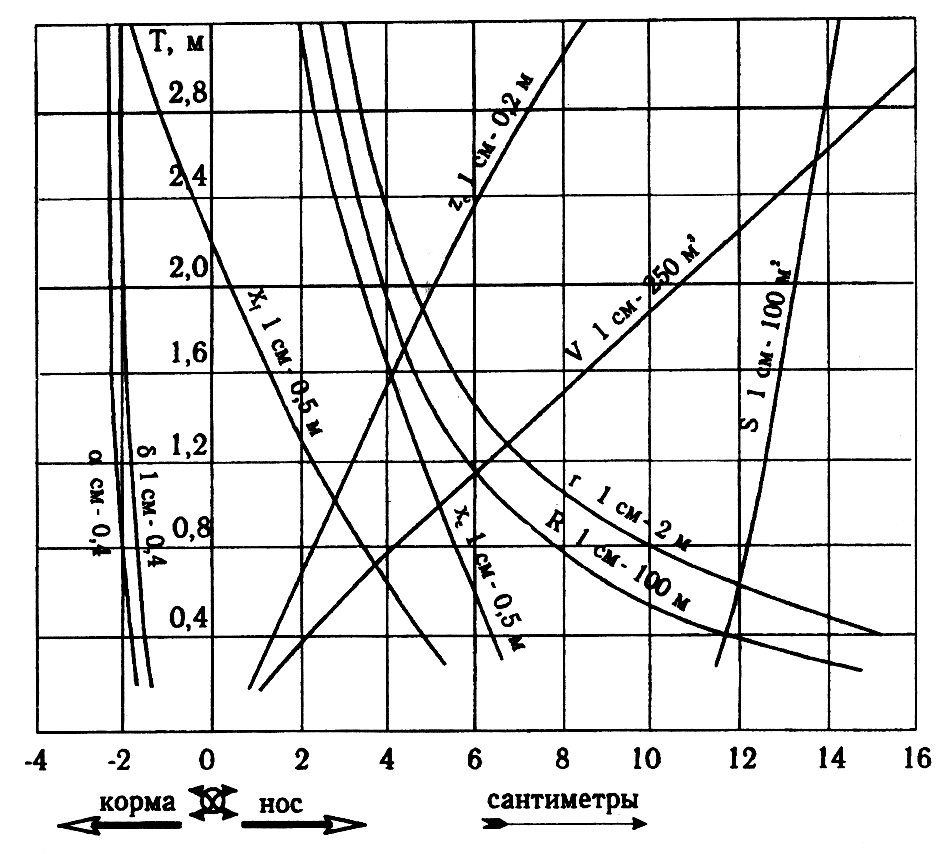
Рис.1.11. Кривые плавучести и начальной остойчивости

При приеме или снятии малого груза (когда форма ВЛ при изменении осадки меняется незначительно) изменение h₀, H₀, k и K подсчитывается по формулам:

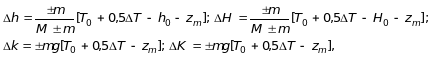(1.10)

где M, T₀ и h₀ - водоизмещение, осадка и НПМВ судна до грузовых операций; - изменение осадки после приема (+) или (-) снятия груза, z_m - аппликата Ц.Т. груза, g=9,81 м/с² - ускорение силы тяжести.

При наличии на судне подвижного груза (незакрепленного, подвешенного, сыпучего или жидкого со свободной поверхностью) остойчивость судна претерпевает изменение и поправки и , учитывающие наличие таких грузов, определяются по формулам (1.11)--(1.13).

При подвешенном грузе массой m:

, (1.11)

где - высота подвески (от ОП).

При сыпучем грузе:

. (1.12)

При жидком грузе со свободной поверхностью:

. (1.13)

Здесь i_x - собственный момент инерции свободной поверхности груза, относительно продольной оси; _гр и _ж- плотность грузов сыпучего и жидкого; - угол естественного откоса сыпучего груза.

Выражения (1.7)--(1.10) пригодны также и для определения поправок к значениям продольной метацентрической высоты и коэффициента остойчивости, однако значения H₀ и K при этом меняются настолько незначительно, что в практических задачах эти изменения обычно не учитывают.

Упражнения

1.9. На пароме, понтон которого имеет форму параллелепипеда с размерами LхBхHхT=12х6х1,7х1,2, при подходе к пристани пассажиры скопились у борта (рис.1.12). Определить, где должно быть расположено леерное ограждение, чтобы запас надводного борта при крене не оказался меньше 0,2 м? Расчетное число пассажиров n=60 чел. (массу одного пассажира принять равной m=80 кГ. Отстояние Ц.Т. всей группы от леера принять 1,0 м. Аппликата Ц.Т. парома z_g=2,3 м.

Решение:

Допустимый угол крена определяется очевидным соотношением:

=0,1 рад.

Кренящий момент, создаваемый пассажирами, равен: , где l - искомое расстояние леера от ДП.

Кренящий момент будет уравновешен восстанавливающим моментом , где вес

Рис.1.12. К упражнению 1.9

судна - D= gLBT=1*9,81*12*6*1,2 =848 кН. Начальная поперечная метацентрическая высота h₀=r+z_c-z_g. z_c=T/2=0,6 м (для параллелепипеда), r=J_x/V. Для параллелепипеда J_x=LB³/12; V=LBT, следовательно, r=B²/(12T)=6²/(12*1,2)=2,5 м. Отсюда h₀=2,5+0,6-2,3=0,8 м. M_B=848*0,8*0,1=67,8 кНм.

Искомое расстояние l определяется из равенства M_кр=M_B:

=2,44 м.

Леерное ограждение должно быть расположено не далее 2,44 м от ДП парома.

1.10. На корабле, кривые элементов которого приведены на рис.1.11, вследствие смещения грузов в трюме образовался крен =3⁰. Аппликата Ц.Т. судна z_g=3,0 м, осадка T=2,0 м. Определить потребное количество груза, которое нужно перенести на палубе, чтобы выпрямить судно, если возможное плечо переноса l=6,0 м.

Решение:

С графиков рис.1.11 при заданной осадке T=2,0 м снимаются значения величин, необходимых для расчета: M= V=2700 т, r=9,0 м, z_с=1,0 м и подсчитывается h₀=r+z_c-z_g=9,0+1,0-3,0=7,0 м. (Пояснение: при пользовании кривыми рис.1.11 отстояние расчетных точек от оси осадок следует определять в единицах измерения, обозначенных на продольной оси). Кренящий момент от смещения груза на правый борт будет равен моменту восстанавливающему при наклонении судна на =3⁰, т.е. M_кр=M_B=Dh₀ =9,81*2700* 7,0*3/57,3=9710 кНм. Момент от перемещенного по палубе груза должен уравновесить кренящий момент от груза, сместившегося в трюме, т.е. должен быть равным по величине восстанавливающему моменту gml=M_B, откуда потребное количество переносимого груза на палубе m=M_B/gl=9710/9,81*6=165 т.

1.11. Морское судно длиной 60 м и водоизмещением M=2800 т сидит без крена и дифферента. Определить осадки оконечностей и угол крена после перемещения груза массой m=50 т из трюма (x₁=5 м, y₁=-2 м, z₁=1,5 м) на палубу (x₂=-10 м, y₂=-4 м, z₂=6,5 м). Известны: T=3,5 м, h₀=0,8 м, z_g0=4,0 м, x_f=-1,2 м, H₀=16 м.

Решение:

Определяются изменение координат Ц.Т. судна в связи с перемещением груза (как элемента системы в упражнении 1.4)

=-0,268 м; =-0,036 м;

=0,089 м.

Изменение аппликаты Ц.Т. приводит к изменению значения h. Новое значение h=h₀- z_g=0,8-0,089=0,711 м. Осадки оконечностей и угол крена можно определить, следуя рассуждениям, вытекающим из рассмотрения схем на рис. 1.13.а и 1.13.б.

Перемещение груза из т.1 в т.2 (см. рис.1.13.а) можно уподобить приложению к судну дифферентующего момента пары сил M_диф=mg(x₂-x₁), который будет уравновешиваться восстанавливающим моментом при некотором угле дифферента т.е. M_диф=M_B ; mg(x₂-x₁)=DH₀ .

б)

а)

Полагая H₀ неизменным, рассчитывается угол дифферента

=

0,0038 рад.

Осадки оконечностей

=3,38 м;

=3,61 м.

Иной подход к решению иллюстрирует рис.1.13.б.

Перенос груза вдоль судна приводит к перемещению Ц.Т. судна, и в этом случае дифферентующую пару составляют силы веса и поддержания , а уравновешивающий момент по-прежнему равен

M_B =DH₀ .

Отсюда =-0,0038 рад.

Рис.1.13. К упражнению 1.11

Рассуждая подобным образом, можно определить и угол крена по выражениям:

а) M_кр=M_B; mg(y₂-y₁)=Dh ; =-0,05 рад  -3⁰.

б) M_кр=M_B; =Dh ; =-0,05 рад  -3⁰.

Знак (-) указывает, что судно накренилось на левый борт. Средняя осадка T=(T_н+T_к)/2=(3,38+3,61)/2=3,5 м.

1.12. На судно, сидящее прямо и на ровный киль с осадкой T_п=1,5 м, принят груз массой m=700 т с координатами x_m=8 м, y_m=0,5 м, z_m=1,8 м. Характеристики судна: B=14,8 м, L=105 м, =0,822, =0,875, z_gп=2,2 м, x_f=0,18 м. Определить параметры посадки судна после приема груза. Недостающие величины определить по приближенным формулам. Изменением коэффициентов полноты пренебречь.

Решение:

Посадка судна, т.е. его положение относительно поверхности воды, определяется тремя параметрами: осадкой, углом крена и углом дифферента.

После приема груза последовательно рассчитываются.

Новая осадка =2,01 м.

Водоизмещение судна с грузом =2568 т.

Метацентрический радиус =8,90 м.

Аппликата Ц.В. =1,04 м.

Аппликата центра тяжести =2,14 м.

Начальная поперечная метацентрическая высота h₀=r+z_c-z_g=8,90+1,04-2,14=7,80 м.

Угол крена из равенства кренящего момента и восстанавливающего момента M_кр=M_B или gmy_m=gMh₀

=0,0175 рад  1⁰.

Продольный метацентрический радиус =365 м.

Продольная метацентрическая высота H₀= H₀=R+z_c-z_g =365+1,04-2,13=364 м.

Угол дифферента из равенства момента дифферентующего и момента восстанавливающего M_диф=M_B, или gm(x_m-x_f)=gMH₀ .

Угол дифферента =0,0059.

Линейный дифферент =0,0059*105=0,62 м.

1.13. Пользуясь кривыми плавучести и остойчивости (рис.1.11), определить осадку судна T и координаты центра тяжести принятого груза массой m=400 т, если после приема судно продолжает сидеть прямо и на ровный киль, а остойчивость судна не меняется. Исходная осадка судна T₀=1,8 м, а аппликата центра тяжести судна до приема груза z_g0=2,1 м.

Решение:

Для определения осадки необходимо найти водоизмещение в грузу, которое равно сумме водоизмещения порожнем и массы груза M=M_п+m.

По кривой V(T) (рис.1.11) при заданной осадке T₀=1,8 м определяется соответствующее значение V₀=2375 м³, а затем M₀= V=2375 т (полагая =1,0 т/м³).

Подсчитывается масса судна в грузу M=M₀+m=2375+400=2775 т, и соответствующее V=M/ =2775 м³.

Осадка судна в грузу при V=2775 по рис.1.11 T=2,12 м.

При =0 (по условию) восстанавливающие моменты равны нулю и, следовательно, отсутствует кренящий и дифферентующий моменты от принятого груза. Можно записать M_кр=mgy_m=0; M_диф=mg(x_m-x_f)=0. Отсюда при m 0, y_m=0 и x_m=x_f. Поскольку по условию остойчивость судна не изменяется, не изменится и коэффициент остойчивости, т.е. k=0.

По формуле (1.10) , откуда .

Площади ватерлиний до и после приема груза определяется по кривой S(T) (рис.1.11) -- S₀=1320 м²; S=1350 м²; средняя площадь S_ср=(1350+1320)/2=1335 м².

Приращение осадки =0,3 м.

Аппликата Ц.Т. принятого груза z_m=2,12+0,5*0,3=2,27 м.

1.14. Определить наибольшие возможные углы крена и дифферента понтона плавучего крана при подъеме груза m=20 т и максимальном вылете стрелы за борт l=8 м. Порожнем понтон сидит прямо и на ровный киль, имея осадку T_п=2,0 м, длину L=35 м, ширину B=12 м. Аппликата Ц.Т. порожнем z_g0=5,3 м. Возвышение нока стрелы над ОП z_н=24 м. Понтон имеет форму параллелепипеда.

Решение:

Последовательно рассчитываются следующие величины.

Водоизмещение порожнем M_п= LBT_п=1*35*12*20=840 т.

Метацентрические высоты (см. упражнение 1.10)

=1,7 м;

=46,7 м.

Приращение осадки м.

Рис.1.14. К упражнению 1.14

Центр тяжести подвешенного груза следует полагать находящимся в точке подвеса, тогда он может считаться закрепленным, и поправки к метацентрическим высотам определятся по формулам (1.10):

=-0,55 м;

=-1,58 м.

Новые значения метацентрических высот h₀₁=1,15м, H₀₁=45м.

Коэффициенты остойчивости

k=g(M_п+m)h₀₁=9,81*860*1,15=9700 кНм; K=g(M_п+m)H₀₁=9,81*860*45=379600 кНм.

Кренящий и дифферентующий моменты от подвешенного груза

M_кр=M_диф=mg(l+B/2)=20*9,81*(8+12/2)=2750 кНм.

Искомые углы дифферента и крена

=M_диф/K=2750/379600=0,7*10^-2 рад=0,4⁰; =M_кр/k=2750/9700=0,284 рад=16⁰.

1.15. На наливной барже с грузом нефти 800 т ( _гр=0,9 т/м³), план палубы которой приведен на рис.1.15, из танка 1 в танк 4 перекачали 200 т нефти. Известны элементы баржи: L= 60 м, B=12 м, T=2,4 м, =0,85, =0,90, z_g=2,5 м. Во всех танках имеется свободная поверхность груза. Определить угол крена и осадки оконечностей. При расчете воспользоваться приближенными формулами (1.8).

.

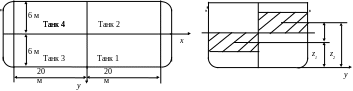
Рис.1.15. К упражнению 1.15

Решение:

По приближенным формулам определяются характеристики остойчивости баржи

.=1,23 м; =5,02 м;

h₀=r+z_c-z_g 5,02+1,23-2,5=3,82 м; =102 м; H₀=R+z_c-z_g=102+1,23-2,5=101 м.

Влияние свободной поверхности груза определяется по формулам (1.13): , где i_x и i_y - собственные моменты инерции площади свободной поверхности относительно продольных и поперечных осей; считая площади свободной поверхности груза прямоугольными, вычисляем эти величины.

=1440 м⁴; =16000 м⁴.

Водоизмещение баржи =1830 т.

Метацентрические высоты баржи с учетом влияния жидких грузов

=3,11 м;

=93 м.

При перемещении части груза из танка 1 в танк 4 плечи переноса определяются из геометрических соотношений (рис.1.15) x₂-x₁=-20 м; y₂-y₁=-6,0 м.

Кренящий и дифферентующий моменты

=-11800 кНм; =-39200 кНм.

Cледует учесть перемещение Ц.Т. по вертикали из-за переноса части груза на величину

=1,86 м,

в связи с чем изменится НПМВ. Окончательно ее величина составит (см. формулы 1.9)

=2,9 м.

Углы наклонений определятся из условий

M_кр=M_B; gm(y₂-y₁)=gMh₀₂ ; ;

=-0,227 рад=-13⁰ (на ЛБ);

=-0,0231 рад=1,3⁰ (в корму).

Осадки оконечностей (при x_f=0 ввиду симметрии относительно миделя)

=1,71 м; =3,09 м.

1.16. На судне после посадки на мель визуальным осмотром установлены осадки оконечностей и угол крена, равные T_н=1,9 м, T_к=2,62 м и =8⁰. Известны элементы судна до аварии: L=60 м, M=1700 т, T=2,7 м, S=445 м₂, x_f=-1,2 м, h₀=1,8 м, H₀=45 м. Определить силу реакции грунта и координаты места контакта.

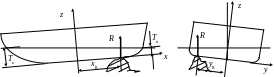
Рис.1.16. К упражнению 1.16

Решение:

Силу реакции грунта R уподобим силе веса груза gm, снятого из точки с координатами (x_R, y_R, 0). Средняя осадка судна после аварии T_ср=(T_н+T_к)/2=(1,9+2,62)/2=2,26 м, изменение осадки составит T=T_ср-T=2,26-2,7=-0,44 м.

Используя выражение , определим силу реакции

=1920 кН.

Поперечная остойчивость судна изменится и новое значение определится согласно формуле (1.10):

=1,65м.

Угол дифферента =(T_н-T_к)/L=(1,9-2,62)/60=-0,012 рад.

Изменением продольной остойчивости можно пренебречь. Кренящий и дифферентующий моменты, определяемые произведением силы реакции на соответствующие координаты, уравновешиваются восстанавливающими моментами. Из этих условий: M_кр=M_B; Ry_R=(gM-R)h₀₁ ; M_диф=M_B ; R(x_R-x_f)=(gM-R)H₀

определяются искомые координаты x_R и y_R.

=-5,35 м;

=1,84 м.

Контрольные вопросы

1. Каково условие положительной начальной остойчивости?

2. Почему судно не обладает остойчивостью, если метацентр совпадает с центром тяжести судна?

3. Какова размерность коэффициентов остойчивости?

4. Два судна имеют одинаковые коэффициенты продольной остойчивости, но разную длину. К какому из судов необходимо приложить больший момент для получения одинакового линейного дифферента?

5. Количественным или качественным показателем является коэффициент остойчивости?

6. Как меняется остойчивость при вертикальном перемещении груза?

7. Как изменится метацентрическая высота и коэффициент поперечной остойчивости при приеме груза в плоскость ГВЛ?

8. Изменится ли начальный угол крена судна при вертикальном перемещении груза?

9. Чем объяснить одинаковое изменение метацентрической высоты при приеме подвешенного груза или помещении его в точке подвеса?

10. Можно ли путем принятия груза увеличить продольную метацентрическую высоту?

11. Как должна располагаться на судне цистерна с жидким грузом: длинной стороной вдоль или поперек судна?

12. Как можно уменьшить влияние жидкого груза?

13. Влияет ли сыпучий груз на остойчивость судна при наклонениях на угол, меньший угла сыпучести груза?

14. Как изменяется коэффициент остойчивости при посадке судна на мель?

Задачи

1.43. Яхта водоизмещением M=20 т имеет момент инерции площади ГВЛ относительно продольной оси J_x=9,4 м⁴. Определить величину коэффициента поперечной остойчивости яхты, если возвышение центра тяжести над центром величины составляет a=0,15 м.

1.44. Судно имеет следующие характеристики: LхBхT=105х14,5х2,5 м, =0,936, =0,860. С помощью приближенных формул определить значения продольной и поперечной метацентрических высот, если аппликата центра тяжести z_g=2,0 м (принять H₀ R).

1.45. Судно после приема груза в точку с координатами x₁=10 м, y₁=0,4 м, z₁=3 м изменило среднюю осадку от T₀=1,5 м до T₁=2,5 м. Определить массу принятого груза, значения коэффициентов остойчивости и параметры посадки судна после приема груза, если до приема z_g0=2,0 м. Недостающие величины снять с кривых плавучести и начальной остойчивости (рис.1.11).

1.46. Морское судно имеет главные размерения L=155м, B=25м, T=10,0м, коэффициенты полноты =0,750, =0,810 и значения аппликат метацентра z_m=11,3 и центра тяжести z_g=10,5 м. Удельный вес морской воды =9,92 кН/м³. Определить момент, кренящий на 1⁰, и крен судна при действии момента кренящего M_кр=25850 кНм.

1.47. Характеристики морского судна L=110 м, B=18,0 м, T=8,20 м, =0,899, z_g=7,4 м, z_m=8,5 м. Определить коэффициент поперечной остойчивости и величину момента, накренившего судно на угол =10⁰. Плотность морской воды принять равной =1,02 т/м³.

1.48. Судно имеет следующие характеристики L=75,0 м, B=8,0 м, =0,775, =0,815, T_н=1,6 м, T_к=2,2 м. Определить момент, дифферентующий судно на 1 см и количество груза, которое необходимо переместить вдоль судна для его спрямления, если плечо перемещения l=20 м (принять H₀ R).

1.49. Главные размерения пассажирского судна LхBхT=30х5,3х1,13 м, коэффициенты полноты =0,453, =0,804. Момент инерции площади ГВЛ J_x=340 м⁴, аппликаты центра величины и центра тяжести судна z_c=0,71 м, z_g=1,94 м. Площадь парусности судна S_п=110 м², возвышение центра парусности над основной плоскостью z_n=2,8 м. Определить угол крена судна при статическом действии ветра с удельным давлением p_a=180 Па; точку приложения силы сопротивления воды боковому дрейфу принять равной 0,25Т от основной плоскости.

1.50. На судне с размерениями L=39,6 м, B=10,0 м, T= 0,92 м и коэффициентом полноты =0,845, груз массой m=36 т и координатами x_гр=-8,0 м, y_гр=-3,0 м, z_гр=3,0 м перемещен так, что новые координаты центра масс судна оказались равными x_g1=-2,92 м, y_g1=0,1 м, z_g1=2,0 м. Определить углы крена и дифферента судна, а также изменение коэффициента поперечной остойчивости, вызванные перемещением груза. Метацентрические высоты до перемещения груза h₀=11,4 м, H₀=188 м.

1.51. Какое количество водного балласта следует перекачать из цистерны правого борта понтона плавучего дока в цистерны левого борта для устранения крена =3,5⁰. Размеры прямоугольного понтона дока LхBхT=120х 30х 3 м, аппликата центра тяжести дока z_g=6,3 м. Расстояние между центрами цистерн 20 м.

1.52. На судно водоизмещением M=300 т и начальной метацентрической высотой h₀=2,2 м приняты 2 груза: один массой m₁=20 т в точку с координатами y₁=-2,2 м и z₁=2,0 м и второй m₂= 30 т в точку с координатами y₂=-1,4 м и z₂=1,8 м. Определить коэффициент поперечной остойчивости и угол крена судна после приема грузов, если первоначальная осадка равнялась T=1,2 м, а площадь ГВЛ - S_гвл=310 м².

1.53. Из салонов, расположенных в корпусе судна, на берег сошло 40 пассажиров, а с главной палубы 50 пассажиров. Координаты центра тяжести пассажиров в корпусе z_корп=0,9 м, а на палубе z_пал=3,0 м. Водоизмещение судна в грузу M=60 т, площадь ГВЛ S=100 м₂, осадка в грузу T=1,1 м. Определить изменение коэффициента поперечной остойчивости, если до выхода пассажиров h₀=2,5 м. Массу одного пассажира принять 80 кг.

1.54. В ходе модернизации танкера с характеристиками LхBхT =60х8х1,2, =0,800, =0,840, z_g=1,9 м с него сняли левый двигатель массой m₁=6 т и координатами z₁=1,14 м, y₁=-2,0 м и переместили по вертикали из трюма на палубу грузовой насос массой m₂=2 т (величина перемещения =2,5 м). Определить угол крена судна в результате проведенных операций.

1.55. На судно, имеющее первоначальную осадку T=1,8 м, принят груз массой m=200 т с координатами y₁=5 м, z₁=1,5 м. Определить, будет ли в результате крена вливаться в открытый иллюминатор вода, если его нижняя кромка находится на высоте 2,5 м над ОП. Ширина судна B=14,5 м, аппликата центра масс до приема груза z_g=2,0 м. Недостающие величины снять с кривых плавучести и остойчивости (рис.1.11).

1.56. Прямоугольный понтон размерами LхBхT =10х2х0,28 имеет в корпусе 2 т воды и человека. Аппликата центра масс z_g=0,12 м. На какое расстояние от ДП к борту должен переместиться человек массой 90 кг, чтобы вода пошла через борт понтона высотой H=0,4 м.

1.57. Определить величину изменения коэффициента поперечной остойчивости танкера водоизмещением 5000 т после того, как на нем, кроме диаметральной, были поставлены еще две боковые продольные переборки на одинаковом расстоянии между бортом и ДП. Длина грузовых танков l=96 м, ширина корпуса B=16,0 м, плотность груза _гр=0,8 т/м³. Все танки имеют прямоугольную форму, и грузовместимость используется не полностью.

1.58. На судне с главными размерениями LхBхT =30х6х1,2 и коэффициентами полноты =0,560, =0,780, из корпуса подручными средствами извлекается двигатель массой m=4 т. Определить максимально возможную высоту точки подвеса грузоподъемного устройства, при которой значение метацентрической высоты упадет ниже 1 м. Начальное значение аппликаты центра тяжести z_g=2,2 м.

1.59. Две прямоугольные в плане балластные цистерны, простирающиеся от ДП до борта и имеющие длину l=20 м, расположены в двойном дне и симметричны относительно ДП. Высота междудонного пространства t=0,8 м. Первоначально балластные цистерны заполнены наполовину, при этом z_g=2,47 м, а главные размерения и коэффициенты полноты равны LхBхT =80х12х3,5, =0,602, =0,860, Определить коэффициенты остойчивости при половинном и полном заполнении балластных цистерн и углы крена в 1-ом и 2-ом случаях при действии кренящего момента M_кр=15600 кНм.

1.60. Судно с главными размерениями LхBхT =100х12х2,2 и коэффициентами =0,840, =0,892 село на мель носовой оконечностью. Замерами установлено, что судно сидит прямо, осадка носом составляет T_н=1,78 м, а кормой -- T_к=2,21 м. Трюмы одинаковы по величине и имеют длину l=18 м каждый. Какое количество груза необходимо равномерно перегрузить из носового трюма в три остальных, чтобы судно самостоятельно сошло с мели (принять z_g=2,63 м).