3.6. Структурная схема системы векторного управления

Система векторного управления имеет два канала:

● канал регулирования момента, в котором контур регулирования активной составляющей тока статора i_sq подчинен контуру регулирования скорости;

● канал регулирования потокосцепления ротора, в котором контур регулирования реактивной составляющей тока статора i_sd подчинен контуру регулирования потокосцепления Ψ_r.

Для придания системе требуемых качеств, необходимо синтезировать регуляторы как в канале регулирования (стабилизации) потока, так и в канале регулирования скорости.

При питании АД от автономного инвертора напряжения не удается синтезировать регуляторы классическим способом вследствие того, что в этом случае сильное влияние на динамику системы оказывают перекрестные связи [1, 8]. Современные системы векторного управления АД, выпускаемые ведущими электротехническими фирмами, строятся на базе программируемого микропроцессорного управления и являются цифровыми. Однако они могут быть представлены своим аналоговым вариантом. Структурная схема такого ЭП показана на рис.3.10. На схеме (рис. 3.10) обозначено: 1 – сигнал задания скорости, U_зс=10 В; 2 – момент сопротивления, равный номинальному моменту двигателя, М_с = М_н; 3 – сигнал задания потокосцепления ротора U_Ψro=10 В, подаваемый с некоторым опережением во времени по отношению к сигналу задания скорости.

3.7. Преобразователи координат

Математическое описание асинхронного двигателя записано для двухфазной модели машины. Реальные двигатели переменного тока чаще всего имеют трехфазную обмотку статора, поэтому возникает необходимость преобразования переменных трехфазной машины к переменным двухфазной модели и, наоборот. При этом, учтем, что один и тот же результирующий вектор МДС может быть создан как двухфазной, так и трехфазной обмоткой.

Рисунок 3.10 – Структурная схема системы векторного управления с компенсацией перекрестных обратных связей объекта управления

Следовательно, возникает задача преобразования реальных переменных х_sa, х_sb, х_sc статора трехфазной машины к ортогональной системе координат (, ), т. е. к реальным переменным статора эквивалентной двухфазной машины. Решение этой задачи существенно осложняется в связи с необходимостью перехода от объекта с тремя фазами к обобщенной модели с двумя фазами. Разница в числе фаз затрудняет выполнение условия инвариантности мощности. Учитывая это, представим реальные переменные трехфазной машины в виде векторов и будем полагать, что преобразованные переменные в осях ,  не равны, а пропорциональны сумме проекций реальных переменных х_sa, х_sb, х_sc на оси , . Схема преобразования переменных для трехфазного асинхронного двигателя приведена на рис. 3.11.

Рис. 3.11 – Схемы преобразования переменных трехфазной машины

На основании построения, показанного на рис. 3.11а), можно записать:

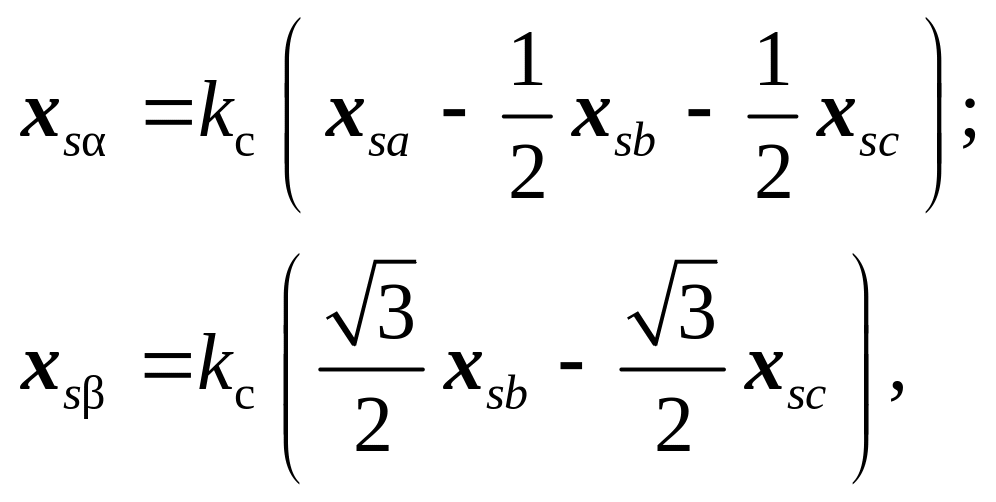(3.45)

где k_c – согласующий коэффициент пропорциональности, выбор которого должен осуществляться из условия инвариантности мощности.

Рассмотрим наиболее распространенный в практике случай, когда переменные трехфазной машины подчиняются условию:

х_sa + х_sb + х_sc = 0. (3.46)

С учетом (3.44) уравнения (3.43) преобразуются к виду

. .47)

Формулы обратного преобразования из неподвижной ортогональной двухфазной системы координат ,  в трехфазную A, B, C можно получить аналогично с помощью рис. 3.11б):

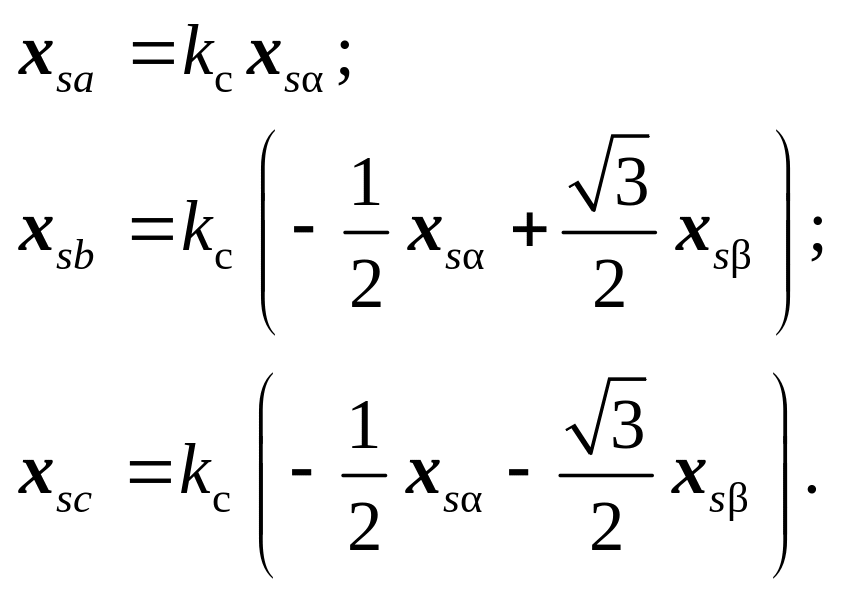(3.48)

Для выполнения условия инвариантности мощности согласующий коэффициент должен быть равен [2].

Для преобразования скалярных переменных записанных в неподвижной системе координат ,  в подвижную систему координат d, q и обратно (рис. 3.12) требуется использовать следующие формулы пересчета:

(3.49)

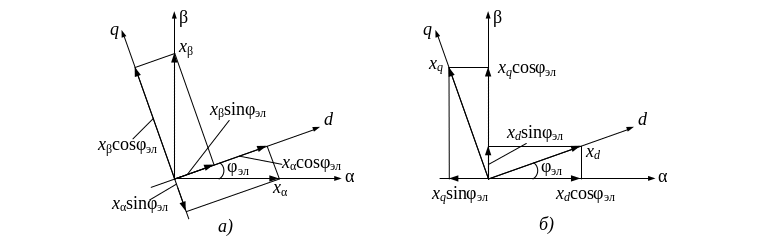
Рис. 3.12 – Векторные диаграммы для преобразования координат:

а) ,  в d, q; б) d, q в , 

(3.50)

где _эл – положение вращающейся системы координат.

Преобразователи координат (ПК) составляют исполнительную часть системы управления. Схема ПК из вращающейся системы координат d, q в неподвижную α, β на основании уравнений (3.50) приведена на рис. 3.13, а схема ПК из двухфазной α, β в трехфазную А, В, С на основании уравнений (3.48) показана на рис.3.14. Используя обе схемы ПК, можно получить реальные токи в фазах асинхронного двигателя [8].

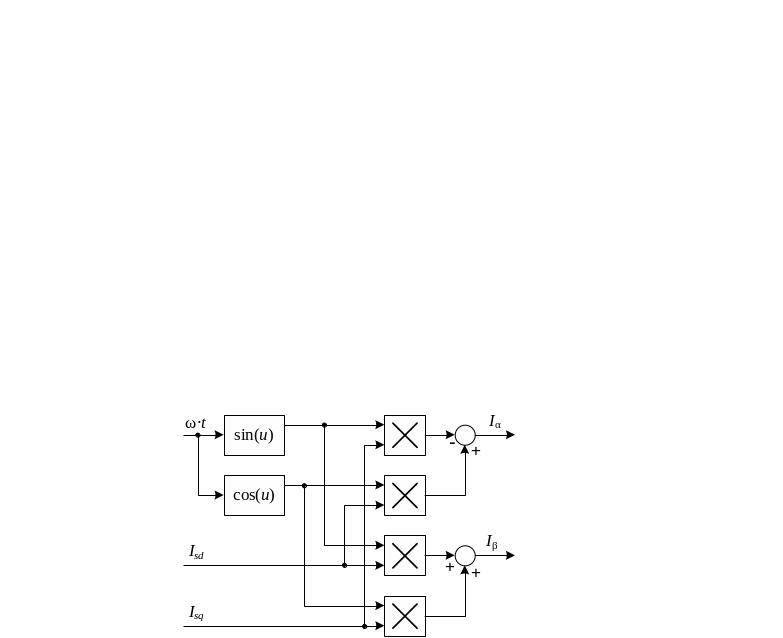
Рисунок 3.13 – Преобразователь координат из двухфазной вращающейся системы d, q в двухфазную неподвижную α, β

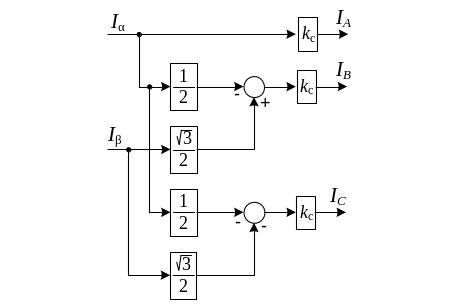
Рисунок 3.14 – Преобразователь координат из двухфазной неподвижной

системы α, β в трехфазную А, В, С с согласующим коэффициентом k_c