3.2. Модели ад в двухфазных ортогональных системах координат

Условием возможности приведения многофазной машины к эквивалентной двухфазной является ее симметрия, поэтому полные сопротивления обмоток фаз статора и ротора обобщенной машины равны. Напряжения питания могут быть несимметричными, при этом для анализа динамики следует пользоваться известным методом симметричных составляющих [2].

При использовании этого метода делаются допущения, которые позволяют линеаризовать электрические цепи АД и тем самым предполагать справедливым использование метода наложения:

● в машине отсутствует насыщение, т. е. ее параметры неизменны;

● статор и ротор машины гладкие, воздушный зазор равномерен;

● напряжение, приложенное к двигателю, ЭДС и токи машины меняются по синусоидальному закону.

Для перехода от математического описания гармонических сигналов в многофазных (трехфазных) координатах к математическому описанию в ортогональных двухфазных координатах d,q используется понятие обобщенного вектора. Обобщенным называют такой вектор , проекции которого на оси фаз равны мгновенным значениям соответствующих фазных величин в заданный момент времени.

Для выполнения этой формулировки обобщенный вектор при угле поворота φ_ν должен вращаться против часовой стрелки с угловой скоростью:

, (3.1)

совпадающей с угловой скоростью соответствующего периодического сигнала и иметь модуль, который равен максимальному значению фазной величины

. (3.2)

На рис.3.2 изображен обобщенный вектор какой-либо физической величины ротора , его проекции на физические оси векторная сумма этих проекций и проекции обобщенного вектора на действительную d (Re) и мнимую q (Im) оси, первая из которых (v_d) совпадает с осью А, а вторая (v_q) – расположена перпендикулярно к первой и повернута на угол 90˚ против часовой стрелки.

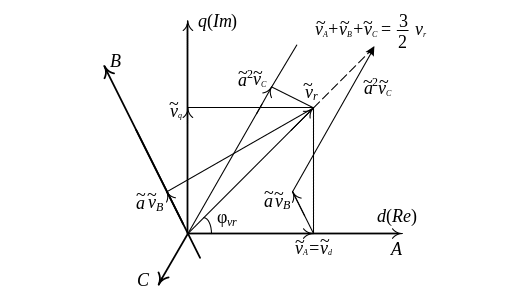
Рисунок 3.2 – Обобщенный вектор и его составляющие

В литературе [1, 6] показано, что сумма векторов представляет собой вектор, который совпадает с обобщенным вектором по направлению и превышает его амплитуду в 1,5 раза. С учетом этого можно записать:

; (3.3)

, (3.4)

где:

а φ_νr – угол между направлением обобщенного вектора ротора и осью d:

. (3.5)

Таким образом, формулы (3.3) и (3.4) описывают обобщенный вектор ротора в трехфазной (abc) и ортогональной (dq) системе координат, которые вращаются со скоростью ротора:

. (3.6)

При исследовании АД используются параметры схемы замещения двигателя, изображенной на рис. 3.3. Она отличается от обычной схемы замещения АД наличием источника ЭДС вращения в цепи ротора двигателя.

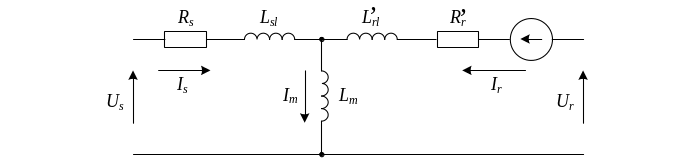
Рисунок 3.3 – Схема замещения АД

На рисунке приняты следующие обозначения:

U_s, i_s – напряжение и ток статора;

R_s – сопротивление обмотки статора;

U_r, i_r – напряжение и ток ротора;

R’_r – приведенное сопротивление обмотки ротора;

L_m – индуктивность от главного (основного) потока двигателя;

L_sl, L’_rl – индуктивность рассеяния обмоток статора и ротора.

Схема обобщенной электрической машины в произвольной системе координат u, v, вращающейся с некоторой скоростью ω_k, приведена на рис. 3.4.

Рис. 3.4 – Схема обобщенной машины в осях u, v

Динамика обобщенной машины описывается четырьмя уравнениями электрического равновесия в цепях ее обмоток и уравнением электромеханического преобразования энергии, которое выражает электромагнитный момент М как функцию электрических и механических координат системы. Уравнения Кирхгофа (электрического равновесия) в системе координат u, v, выраженные через потокосцепления , имеют вид:

(3.7)

где ω_k – скорость вращения системы координат; Ψ_s – потокосцепление статора; Ψ_r – потокосцепление ротора.

Потокосцепления обмоток определяются результирующим действием токов всех обмоток статора и ротора:

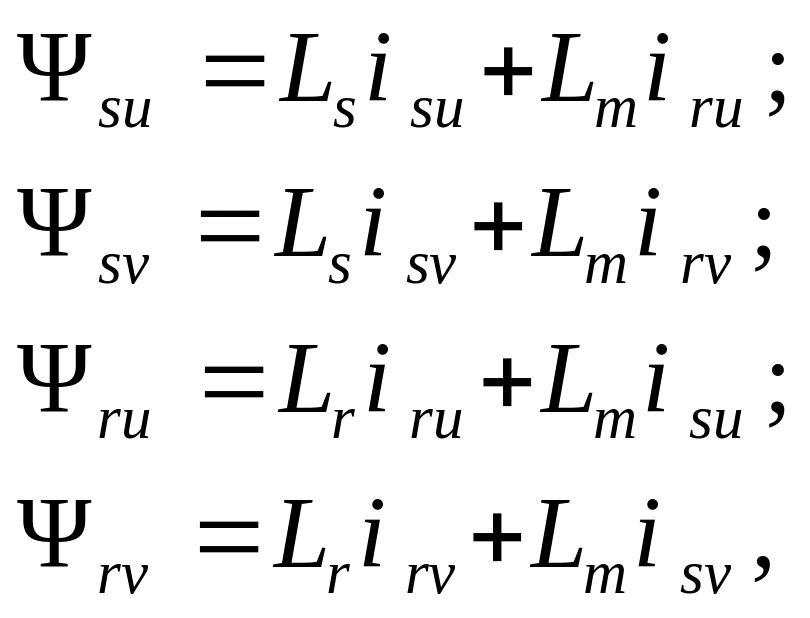, (3.8)

где .

Из уравнения (3.8) определим токи обмоток статора и ротора:

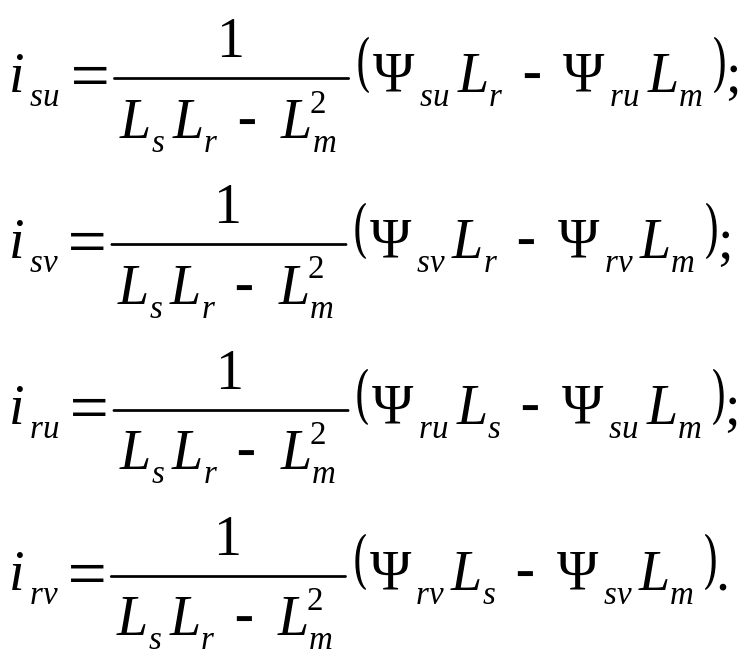(3.9)

В теории электромагнитных переходных процессов электрических машин в ортогональных осях обычно применяются три координатные системы, являющиеся частным случаем системы координат, вращающейся с произвольной скоростью ω_k:

● система координат α, β, неподвижная относительно статора ω_k = 0;

● система координат x, y, неподвижная относительно ротора и вращающаяся относительно статора с частотой вращения ротора ω_k = ω_r;

● система координат d, q, вращающаяся относительно статора с синхронной скоростью и являющаяся неподвижной относительно поля статора асинхронной машины, в этом случае ω_k = ω_0эл.

Переход к модели с двумя взаимно неподвижными обмотками существенно упрощает математическое описание динамических процессов электромеханического преобразования энергии. Коэффициенты взаимной индукции и потокосцепления взаимно неподвижных обмоток становятся независимыми от механической координаты, а движение реальных обмоток и вращение координатных осей учитываются в уравнениях электрического равновесия введением дополнительных ЭДС вращения. При этом значительно упрощается уравнение электромагнитного момента двигателя, в котором устраняется непосредственная зависимость от угла _эл и электромеханическая связь проявляется посредством зависимости токов и потокосцеплений обмоток от скорости двигателя.

3.2.1. Модель в системе координат α, β

Система координат α, β применяется для анализа систем электропривода с управлением двигательными и тормозными режимами асинхронных машин по цепи статора, в том числе при анализе систем с векторным управлением и для исследования режимов при несимметрии статорных цепей. При моделировании АД с питанием от источников несинусоидального напряжения используются модели в естественных осях A, B, C и α, β. Обычно положение оси α совпадает с магнитной осью одной из фаз реальной машины, при этом эквивалентный ток будет равен реальному фазному току двигателя. Выбор _k = 0 обеспечивает преобразование реальных переменных ротора, выраженных в осях u, v к неподвижным осям , , связанным со статором машины.

Определенную сложность при построении модели АД в системе координат α, β представляет то обстоятельство, что эквивалентные напряжения и изменяются во времени по синусоидальному закону с постоянной частотой источника электроэнергии ω_0эл = 2f_с, рад/с.

При этом величины напряжений, приложенных к обмоткам статора, равняются соответственно: ,

, (3.10)

где U_max = 311 В – амплитудное значение напряжения.

Структурная схема для моделирования соответствующих напряжений статора представлена на рисунке 3.5.

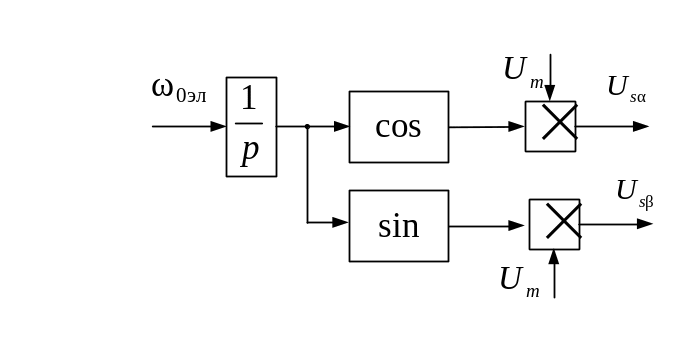
Рисунок 3.5 – Схема задания напряжения статора

Уравнения электрического равновесия в осях ,  принимают вид [2]:

(3.11)

3.2.2. Модель в системе координат x, y

Систему координат x, y используют преимущественно для исследования режимов синхронных и асинхронных машин при несимметрии ротора. Она наиболее целесообразна при расчете систем электропривода с машинами двойного питания, например, каскадных схем управления АД с фазным ротором. При этом статорные и роторные переменные изменяются по синусоидальному закону с частотой скольжения двигателя.

В синхронных машинах в статических режимах работы _0.эл = _эл, поэтому использование системы координат x, y позволяет оперировать соотношениями, аналогичными постоянному току.

Выбор _k = _эл = ω_r соответствует преобразованию реальных переменных машины к осям x, y, жестко связанным с ротором машины. При таком преобразовании напряжения и токи являются переменными величинами, но имеют как в роторной, так и в статорной обмотке частоту тока ротора _r.эл = _0.эл – _эл. Проекции вектора напряжения на координатные оси x и y определяются выражениями:

,

. (3.12)

На рис. 3.6 изображена структурная схема формирования питающих напряжений обмоток статора и :

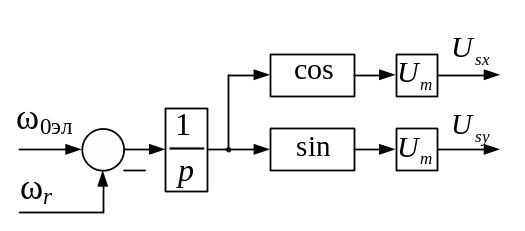
Рисунок 3.6 – Структурная схема модели источника синусоидального

напряжения переменной частоты

Уравнения электрического равновесия в осях x, y принимают вид:

(3.13)

Выражения (3.11) и (3.13) показывают, что выбором системы координат можно исключить ЭДС вращения (ω_элΨ), но только в одном из уравнений. Полагая _k = 0, получим уравнения в неподвижной системе координат α, β с исключением ЭДС вращения только в уравнениях статора. В системе координат x, y, вращающейся синхронно с ротором _k = _эл = ω_r, ЭДС вращения обращается в нуль в уравнениях ротора.

3.2.3. Модель в системе координат d, q

Третью систему координат d,q целесообразно использовать только для исследования симметричных режимов асинхронных машин, если ее применение приводит к упрощению описаний возмущающих воздействий.

Модели d,q, так же как и x,y, привязаны к скорости поля статора (или ротора), что ограничивает область их применения только случаями питания статора АД синусоидальным напряжением. В противном случае требуется разложение несинусоидального напряжения на сумму гармонических составляющих, что увеличивает время моделирования. Этим усложняется модель при анализе переходных процессов, так как на каждом шаге расчета приходится делать разложение на гармонические составляющие. Момент на валу АД рассматривается как сумма моментов от каждой гармоники напряжения питания, что во много раз усложняет расчет.

Выбор _k = _0.эл позволяет осуществить преобразование к осям d, q, вращающимся с синхронной скоростью поля машины. При этом уравнения электрического равновесия записываются так [1, 2]:

(14)

К реальным обмоткам статора приложена симметричная двухфазная система напряжений. При ω_k = ω_0эл и φ_k = ω_0элt выражения для напряжений имеют вид:

(3.15)

Таким образом, в синхронно вращающихся осях d, q реальные переменные напряжения, приложенные к обмоткам статора, при принятой начальной фазе преобразуются в постоянное напряжение U_{s max} = const, приложенное к обмотке, расположенной на оси d. Переменные токи статора и ротора преобразуются в постоянные. Они представляются амплитудными значениями и не содержат гармонических составляющих.

Система d, q часто применяется для моделирования асинхронных машин со скалярным частотно-токовым и векторным управлением. При построении таких систем регулирования асинхронным электроприводом эта система координат наиболее целесообразна, поскольку в ней амплитуда и частота входного напряжения, приложенного к статорным обмоткам, присутствует в явном виде. Вычислительные операции для выявления ненаблюдаемых координат двигателя здесь также существенно упрощены из-за отсутствия в статорных и роторных цепях гармонических составляющих.