4. Контрольные вопросы (примерные):

4.1. Сущность явления внутреннего трения в газах и в жидкостях.

4.2. Напишите формулу Пуазейля и объясните, при каких условиях она справедлива.

4.3. Что такое длина свободного пробега молекул газа? Как её рассчитать, используя данные эксперимента?

4.4. Что такое эффективный диаметр молекул?

4.5. В чём сущность метода измерения коэффициента внутреннего трения газа в данной работе?

4.6. В каких единицах измеряется коэффициент внутреннего трения газа?

4.7. Какие явления переноса существуют и каким законам подчиня­ются?

5. Литература:

5.1. И.В.Савельев, Курс общей физики, т.1, Москва, «Наука», 1977г., с.395.

5.2. А. А. Детлаф, Б.М.Яворский, Я.Б. Милковская, Курс физики, т.1.

5.3. Физический практикум под редакцией В. И. Ивероновой. 5.4. Приложение к данной работе.

Приложение

ЭЛЕМЕНТЫ ФИЗИЧЕСКОЙ КИНЕТИКИ

1. Средняя длина свободного пробега, эффективный диаметр

молекул.

При формулировке ряда задач физической кинетики существенное значение имеет характер взаимодействия молекул. В газах это взаимодействие осуществляется путем столкновения молекул. В течение зна­чительных промежутков времени молекулы находятся сравнительно дале­ко друг от друга и их взаимодействие пренебрежимо мало. Молекулы вступают во взаимодействие лишь на короткие промежутки времени, во время их «столкновений». В противоположность этому, молекулы жидкос­ти находятся в непрерывном взаимодействии и поэтому нет смысла рас­сматривать отдельно "столкновения" молекул жидкости.

В тех случаях, когда применимо понятие столкновений молекул, можно ввести важную характеристику газа в данном состоянии - длину свободного пробега молекул . Эта величина представляет собой среднее расстояние между двумя последовательными столкновениями. Для среднего времени между двумя столкновениями молекул имеем

, (1)

где - величина средней скорости теплового движения молекул. Тогда среднее число столкнове­ний молекулы за 1секунду

(2)

Будем считать "столкновением" только такое сближение одной молеку­лы с другой, при котором взаимодействие изменяет скорость этих мо­лекул по величине и по направлению. Расстояние между центрами молекул, при котором взаимодействие становится существенным, называется эффективным диаметром молекул (рис.1-П). Величина называется эффективным сечением столкновений. Сечение - это площадь вокруг данной мо­лекулы, куда должен попасть центр другой молекулы, чтобы она испытала столкновение. Рассмотрим некоторую молеку­лу с эффективным диаметром , движущуюся со скоростью .

После каждого столкновения молекула, вообще говоря, меняет направление своего движения, на мы предположим для простоты, что этого не происходит. Кроме того, допустим, что все молекулы, кроме данной, неподвижны. Тогда в единицу времени рассматриваемая молекула

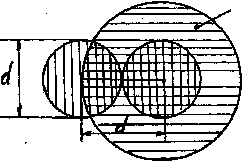
Рис. 1-П.

столкнётся на своем пути с теми молекулами, центры которых лежат внутри цилиндра длиной U, радиусом d и осью, совпадающей с вектором . Число таких молекул, а значит и число столкновений, равно

z= d² u n, (3)

где n- число молекул в единице объёма.

При более строгом подсчёте, с учётом движения всех молекул, получим

z = d² n

Средняя длина свободного пробега молекулы равна

=u/z = u/ d²un = 1/ d² n = 1 / n (4)

2. Явление переноса

Явления переноса в физике - это явления, направленные на установление состояния равновесия.

Если молекулы отличаются одна от другой какой-либо характерной величиной (массой, энергией, импульсом и др., причём их распределе­ние по значениям указанных характеристик неоднородно, то вследствие теплового движения молекул эта величина переносится из одного ме­ста в другое. В результате возникает поток рассматриваемой величины. Пусть G - переносимая величина и пусть она распределена вдоль оси X неравномерно. Рассмотрим площадку ΔS , перпендикулярную к оси X (рис.2-П). За единицу времени через эту площадку вследствие теплового движения пройдёт некоторое количество молекул справа на­лево и обратно, что вызовет поток величины G через данную пло­щадку. Будем считать поток положительным, если величина G пере­носится в положительном направлении оси X и отрицательным, если она переносится в обратном направлении. Вместе с тем, перенос происхо­дит из точек с большей величиной G в точки с меньшей её величи­ной, и потому знак потока должен быть обратным знаку производной или градиенту величины G.

Напомним, что градиентом G называется

(5)

Так как по условию G есть функция только координаты X , то условно можно принять, что - градиент G . Тогда величина потока G через площадку ΔS за единицу времени будет равна

, (6)

где - коэффициент, характеризующий процесс переноса.

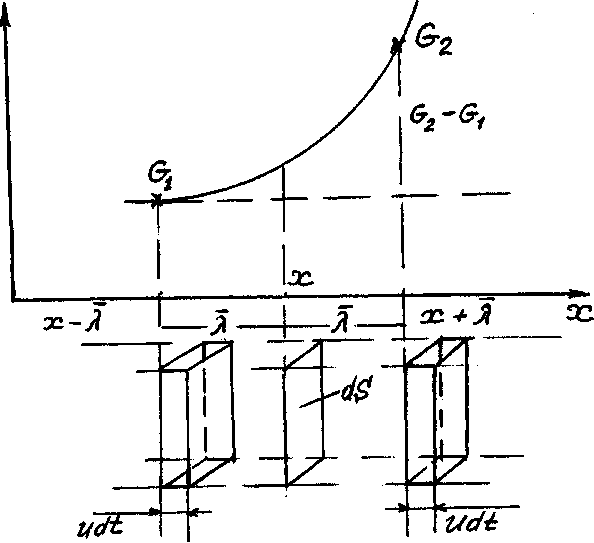
Рис. 2-П.

Рассмотрим явления переноса в газах в рамках молекулярно-кинетической теории. Возьмём два слоя, параллельных площадке ΔS, на расстояниях справа и слева от неё, где - средняя длина свободного пробе­га, G₁ и G₂ - значения величины G в этих слоях. Если U - средняя скорость моле­кул, то слева направо перейдут за время все молекулы, движущиеся в направлении положительной оси X и находившиеся в момент t внутри слоя толщиной . Число таких молекул составляет 1/6 от полного их числа в слое. Так как объём слоя есть , а число молекул в единице объёма равно n, то за время перейдёт слева направо молекул. Поскольку - средняя длина свободного пути, каждая молекула пролетит это расстояние без столкновения и перенесёт с со­бой именно величину G₁. Все молекул перенесут за величину

(7)

В обратном направлении будет за аналогично перенесена вели­чина

(8)

Тогда поток величины G через будет равен

(9)

Будем предполагать, что градиенты переносимой величины малы, тогда приближённо

(10)

Следовательно,

(11)

Сравнивая выражения (6) и (11), получаем следующее значение коэффициента переноса для газов с точки зрения молекулярно-кинетической теории:

(12)

3. Диффузия

Если концентрация газовой смеси или раствора различна в раз­личных точках, то вследствие теплового движения молекул происходит выравнивание концентраций. Вещество, концентрация которого С в данном месте повышена, переходит в места с меньшей концентрацией. Этот процесс называется диффузией. Если градиент концентрации ве­щества вдоль оси X равен , то согласно общему соотношению (6) для диффузионного потока Ф_G через площадку имеем

, (13)

где D – коэффициент диффузии. Заметим, что наряду с молекулярным процессом - диффузией - перемешивание жидкости или газа может происходить в результате микроскопических процессов. Если, например, осторожно капать слой жидкости поверх слоя более плотной жидкости, то возникают струи и жидкости перемешиваются гораздо быстрее, чем в процессе диффузии. Подобный процесс называется конвекцией.

В случае газов коэффициент диффузии можно связать с величина­ми, характеризующими состояние газа и его свойства. Рассмотрим смесь двух газов, общее давление которой во всех точках одинаково, а состав меняется вдоль оси X. Для простоты можно полагать, что молекулы обеих компонент мало отличаются по массе и эффектив­ным сечениям , то есть ; . Тогда молекулам этих компонент можно приписать одинаковую среднюю скорость U, а среднюю длину свободного пробега считать равной

,

где - полное число молекул в единице объёма смеси. "Переносимой величиной" в случае диффузии является концентрация молекул данного (например, первого) сорта, то есть

(14)

Используя формулу (11) для диффузионного потока, получим выраже­ние

(15)

Сравнивая (15) и (13), находим

(16)

Для потока в единицу времени через единицу поверхности имеем:

(17)

Эта формула выражает закон Фика. Таким образом, коэффициент диф­фузии D имеет размерность [D] = м²/с.

Подставляя в последнее соотношение значение длины свободного про­бега из (4), получаем

~ U/ (18)

Если воспользоваться уравнением состояния идеального газа, то

и, следовательно,

, (19)

то есть коэффициент диффузии при заданной температуре обратно пропорционален давлению. Если молекулы значительно различаются по своим массам и размерам, то приведенные выше расчёты требуют уточ­нения. Более детальное рассмотрение показывает, что процесс диф­фузии определяется наибольшей из тепловых скоростей молекул, то есть скоростью молекул наименьшей массы, а для эффективного сече­ния нужно принять наибольшее его значение.

4. Теплопроводность.

Известно, что если в разных точках произвольного тела темпера­тура различна, например, изменяется от слоя к слою, то вследствие явления теплопроводности температура во всём теле выравнивается. Макроскопически явление теплопроводности заключается в процессе пе­реноса некоторого количества тепла от более горячего слоя к более холодному. В газах это явление обычно осложняется переносом тепла струями газа (конвекцией), возникающими из-за того, что слои газа при разных температурах имеют разную плотность.

В рамках молекулярно-кинетической теории процесс теплопровод­ности заключается в том, что молекулы из более горячего слоя, где они имеют большую кинетическую энергию, проникают в более холодный слой и переносят свою кинетическую энергию, что создаёт поток теп­ла.

Таким образом, в данном случае в общей формуле (6) Ф_G - есть поток тепла. Переносимой величиной G в случае явления теплопроводности является количество тепла, то есть G = C_vT, где C_v - теплоёмкость вещества.

В соответствии с общей формулой (6) можно записать (считая, что температура меняется только вдоль оси X)

(20)

или, считая, что поток , запишем

(21)

Поток тепла через единичную поверхность в единицу времени

, (22)

где k - коэффициент теплопроводности.

Этот закон носит название закона Фурье.

Знак (-) здесь указывает, что направление теплового потока противоположно направлению возрас­тания температуры.

Если тепловой поток измеряется в Дж/с, то согласно формуле (21), коэффициент теплопроводности имеет размерность [k] = Дж/м∙с∙К .

В случае газов мы можем применить к процессу теплопроводности об­щую формулу переноса (11). Подставляя в неё , где - теплоёмкость, рассчитанная на одну молекулу, находим

(23)

Согласно последним двум соотношениям коэффициент теплопроводности равен

(24)

Этому выражению можно придать другой вид. Умножим и разделим пра­вую его часть на массу молекулы . Поскольку - число молекул в единице объёма, то - есть плотность газа, а - удельная теплоёмкость газа при пос­тоянном объёме. Следовательно,

(25)

Так как коэффициент теплопроводности пропорционален теплоёмкос­ти газа, он зависит от числа и типа степеней свободы молекулы. Под­ставляя в формулу (24) значение длины свободного пробега , на­ходим

k ~ (26)

Это соотношение показывает, что, в отличие от коэффициента диф­фузии D, коэффициент теплопроводности газа k не зависит ни от давления, ни от плотности. Зависимость k от температуры определяется зависимостью от неё средней скорости молекул U, а также более слабой зависимостью от температуры эффективного сечения и теплоёмкости .

5. Вязкость.

Рассмотрим поток газа, в котором скорость течения U неизменна по направлению, но меняется по величине вдоль перпендикуляра к направлению скорости. Выберем в качестве направления оси X направление этого перпенди­куляра, тогда скорость пред­ставляет собой .

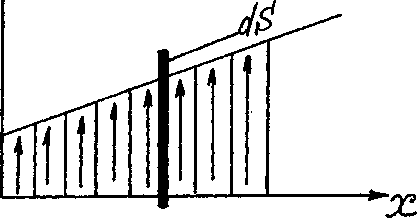
Рис.3-П.

Как показано на рис.3-П, поток газа можно разделить на слои, которые движутся со скорос­тями, параллельными друг дру­гу. Вследствие теплового дви­жения молекулы газа могут переходить из одного слоя в другой, перенося импульс своего направленного движения. В резуль­тате возникает процесс переноса импульса из слоёв, где скорость больше, в слои, где она меньше. Этот процесс, приводящий к вырав­ниванию скоростей течения разных слоёв, называется внутренним тре­нием, или вязкостью.

Используем общую формулу (6) для переноса импульса.

Переносимой величиной является импульс, то есть , где - масса молекулы. Подставляя это значение G в формулу (6) , находим:

(27)

Величина называется коэффициентом вязкости, или коэффициен­том внутреннего трения. Для газов, учитывая (11), получаем:

(28)

Следовательно,

(29)

Выражение (27) может быть отнесено к единице поверхности и к едини­це времени, тогда поток импульса имеет вид:

, (30)

носящий закон Ньютона.

Используя выражение для средней длины свободного пробега (4), мож­но записать формулу для коэффициента вязкости в виде:

~ (31)

Размерность потока Ф_G есть размерность импульса, делён­ного на м² и на секунду, то есть

[Ф ] =

Размерность с^-1 , поэтому [ ] = .

К задаче о вязкости среды можно подойти с другой точки зрения, оправдывающей второе название - коэффициента внутреннего трения. Рассмотрим течение жидкости (или газа) в канале или труб­ке. Во всех реальных случаях жидкость течёт, соприкасаясь с твёр­дой стенкой. Слой жидкости, непосредственно прилегающий к стенке, остаётся неподвижным; он как бы "прилипает" к ней и удерживается силами межмолекулярного взаимодействия. Поэтому в жидкости возни­кает градиент скорости, который изменяется от нуля (на стенке) до некоторого максимального значения в центральных областях трубы. Соответственно, возникает поток импульса в направлении от центра трубы к стенке.

Согласно общим законам механики изменение импульса тела со временем равно силе, действующей на тело. Импульс, передаваемый от слоя к слою жидкости и, в конце концов, от жидкости к стенке, также приводит к появлению силы, называемой силой трения. Можно сказать, что при течении слоёв жидкости или газа с различными скоростями между слоями возникают силы: более быстрый слой «ускоряет» соседний с ним более медленный, а более медленный, наоборот, «замедляет» более быстрый. Возникающие при этом силы внутреннего трения касательны к слоям жидкости. Величина этих сил определяет­ся формулой:

(32)

Отсюда следует, что коэффициент внутреннего трения (вязкости) численно равен силе внутреннего трения, действующей на еди­ничную площадку соприкасающихся слоёв жидкости или газа при гра­диенте скорости, равном с^-1 .

Существуют два существенно различных вида течения вязкой жид­кости или газа. Дня одного из них характерно сохранение слоёв: жидкость как бы разделяется на слои, которые скользят друг отно­сительно друга, не перемешиваясь. Этот вид течения жидкости назы­вается ламинарным (слоистым). Для второго вида течения жидкости характерно быстрое перемешивание. Такое течение называется турбу­лентным.

Ламинарное течение жидкости стационарно, оно характеризуется определённым распределением скоростей по сечению потока жидкости. В противоположность этому, турбулентное течение нестационарно. При таком течении скорость частиц в каждом данном месте всё время из­меняется беспорядочным образом. Поэтому турбулентное течение опи­сывается средней по времени скоростью течения в каждой точке се­чения потока жидкости.

Важной характеристикой движения жидкости является число Рейнольдса (Re), которое определяется следующим образом:

Re = (33)

Здесь и , как обычно, - плотность и вязкость жидкости, U - средняя скорость течения, - величина, характерная для поперечного сечения потока (например, при течении жидкости по трубе есть радиус трубы). Число Рейнольдса (Re) пред­ставляет собой безразмерную величину. При малых его значениях течение жидкости ламинарное. При некотором значении Re, называемым критическим, течение становится турбулентным. Существен­но, что характер течения различных жидкостей или газов в трубах разного радиуса совершенно одинаков, если течению соответствует одно и то же значение Re .

16