
Лабораторная работа № 14 «Определение времени и средней силы соударения упругих шаров»
Цель работы: изучить применение законов сохранения к теории абсолютно упругого и абсолютно неупругого ударов; экспериментально определить среднее время и среднюю силу соударения упругих шаров.
Приборы и принадлежности:
Опытная установка.
Генератор импульсов.
Счетчик импульсов ПСО2 – 4.
Источники постоянного напряжения на 6В и 12В, и переменного напряжения на 220В.
Соединительные провода.
Краткая теория
Основными законами сохранения для замкнутой системы тел (материальных точек) являются: закон сохранения энергии и закон сохранения импульса (момента импульса).
Замкнутой, или изолированной системой
тел (материальных точек) называется
система, на которую не действуют внешние
силы или действие их скомпенсировано
(![]() ).
).
Закон сохранения импульса:
В изолированной системе геометрическая сумма импульсов входящих в нее тел остается постоянной.
![]()
где
![]() и
и
![]() - масса и скорость
- масса и скорость
![]() -ой
материальной точки системы, состоящей
из
-ой
материальной точки системы, состоящей
из
![]() точек.
точек.
Общий закон сохранения энергии:
энергия никогда не исчезает и не возникает из ничего, она переходит от одного тела к другому, из одной формы в другую.
Эти основные законы сохранения используются для установления соотношений между различными величинами при столкновениях (взаимодействиях) тел.
Ударом называется кратковременное взаимодействие тел, возникающее в результате их столкновения.
Удар называется центральным, если силы, возникшие при взаимодействии тел, проходят через их центры масс.
Абсолютно упругий удар - это такой удар, в результате которого механическая энергия соударяющихся тел не преобразуется в другие виды энергии. При этом не происходит потери механической энергии: кинетическая энергия движущихся тел переходит в потенциальную энергию упругой деформации; затем тела восстанавливают свою первоначальную форму и потенциальная энергия опять переходит в кинетическую. После удара происходит перераспределение кинетической энергии и тела движутся с разными скоростями.
Пусть два абсолютно упругих шара с
массами
![]() и
и
![]() движутся до удара поступательно со
скоростями
движутся до удара поступательно со
скоростями
![]() и
и
![]() ,
направленными вдоль оси ОХ, проходящей
через их центры масс. Соударение может
произойти: 1) если шары движутся навстречу
друг другу, или 2) один из шаров догоняет
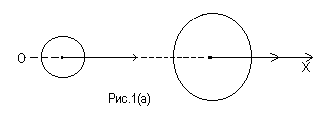
другой. Рассмотрим второй случай (рис.
1, а). Тогда
,
направленными вдоль оси ОХ, проходящей
через их центры масс. Соударение может
произойти: 1) если шары движутся навстречу
друг другу, или 2) один из шаров догоняет
другой. Рассмотрим второй случай (рис.
1, а). Тогда
![]() >
>
![]() > 0. Определим скорости шаров
> 0. Определим скорости шаров
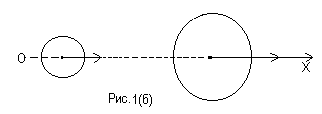
![]() и
и
![]() после удара (рис. 1, б).
после удара (рис. 1, б).

![]()
![]()
![]()
![]()
![]()
![]()
Считаем, что шары образуют замкнутую
систему, и вращение шаров отсутствует.
Запишем уравнение закона сохранения
импульса:
Так как все скорости направлены вдоль
оси ОХ, то это выражение можно заменить
следующим алгебраическим уравнением:
(1*)
![]() (1)
(1)
где
![]() - проекции соответствующих векторов
скоростей на линию удара – ось ОХ.
- проекции соответствующих векторов
скоростей на линию удара – ось ОХ.
Потенциальную энергию шаров до и после удара можно считать равной нулю, так как шары не деформированы. Следовательно, выполняется закон сохранения кинетической энергии:
![]() .
(2)
.
(2)
Сокращая уравнение (2) на 2, запишем
уравнения (1*) и (2), как систему,
которую необходимо совместно решить
для определения скоростей
![]() и
и
![]() .
.
![]()
Перенесем слагаемые, относящиеся к
![]() влево, а к
- вправо:
влево, а к
- вправо:
![]()
(2*)
Разделим уравнение (2*) на уравнение (1*):
![]()
Умножим последнее равенство на и сложим с уравнением (1*):
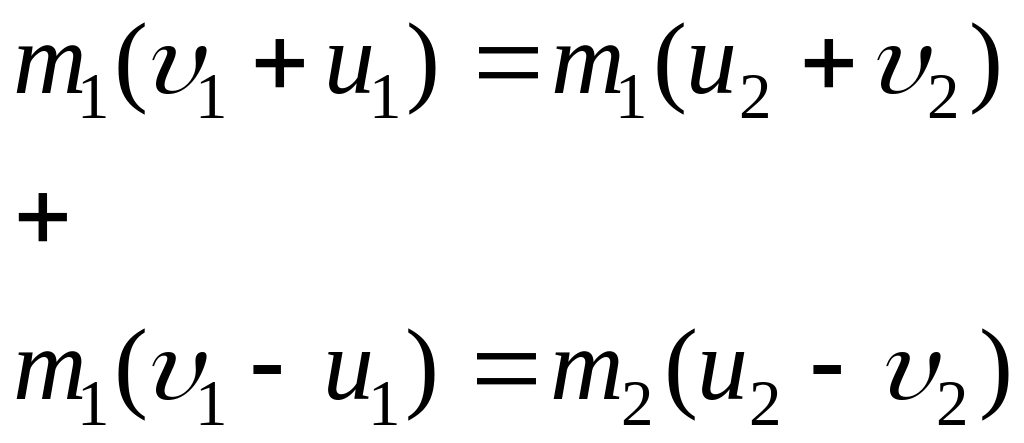
Получим:
![]() .
.
Откуда
![]() .
(3)
.
(3)
Аналогично можно получить:
![]() .
(4)
.
(4)
Рассмотрим частные случаи.
а) Массы шаров одинаковы:
![]() .
Тогда из выражений (3) и (4) имеем
.
Тогда из выражений (3) и (4) имеем
![]() ,
то есть при ударе шары обмениваются
скоростями. Если в частности до удара
второй шар был неподвижен (
,
то есть при ударе шары обмениваются
скоростями. Если в частности до удара
второй шар был неподвижен (![]() ),
то после удара первый шар остановится
(
),
то после удара первый шар остановится
(![]() ),
а второй шар будет двигаться со скоростью
первого (
),
а второй шар будет двигаться со скоростью
первого (![]() )
в том же направлении.
)
в том же направлении.
б) Масса второго шара во много раз больше массы первого шара ( ). Тогда из выражения (3) следует, что
![]() (5)
(5)
Скорость более массивного шара почти
не меняется
![]() .
.
Из выражения (4) получим:
![]() .
(6)
.
(6)
В частном случае, если более массивный
шар покоился
,
то
![]() а
а
![]() (из выражения (5)), то есть скорость более
легкого шара в результате удара изменяется
только по направлению и шар, отскочив,
движется в обратную сторону со скоростью
(из выражения (5)), то есть скорость более
легкого шара в результате удара изменяется
только по направлению и шар, отскочив,
движется в обратную сторону со скоростью
![]() .
Например, упругий удар молекулы о стенку
сосуда.
.
Например, упругий удар молекулы о стенку
сосуда.
Абсолютно неупругий удар - это такой удар, в результате которого тела не восстанавливают свою первоначальную форму, при этом часть кинетической энергии переходит в энергию деформации и в конечном счете - в тепловую (внутреннюю) энергию. После удара тела движутся как одно целое, то есть с одинаковой скоростью.
При абсолютно неупругом ударе выполняется закон сохранения импульса. Закон же сохранения механической энергии не соблюдается: имеет место общий закон сохранения полной энергии - механической и внутренней.
Пусть два неупругих тела с массами
и
![]() движутся вдоль оси ОХ, проходящей
через их центры масс, со скоростями
движутся вдоль оси ОХ, проходящей
через их центры масс, со скоростями
![]() и
и
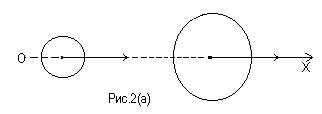
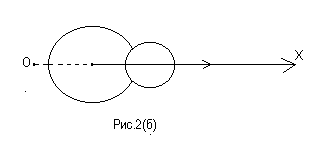
![]() вдоль этой оси (рис. 2, а). Тогда после
центрального абсолютно неупругого
удара их общая скорость поступательного
движения будет
вдоль этой оси (рис. 2, а). Тогда после
центрального абсолютно неупругого
удара их общая скорость поступательного
движения будет
![]() ,
направленная также вдоль оси ОХ (рис.
2, б).
,
направленная также вдоль оси ОХ (рис.
2, б).
Для определения скорости тел после удара достаточно записать закон сохранения импульса:
откуда
Закон сохранения полной энергии для абсолютно неупругого удара запишется так: |
![]()
![]()
![]()
![]()
![]()
.
![]() ,
(9)
,
(9)
где
![]() - энергия, затраченная на деформацию
тел. Определим
.
- энергия, затраченная на деформацию
тел. Определим
.
![]() .
.
Подставляя в последнее выражение
значение скорости
![]() из формулы (8), получим:
из формулы (8), получим:
![]() . (10)
. (10)
На практике используют абсолютно неупругий удар для изменения формы тел (ковка, штамповка, клепка и т.п.), для перемещения тел в среде (забивание гвоздей, свай и т.п.). В первом случае необходимо, чтобы энергия , затраченная на деформацию, была бы наибольшей. Это возможно, если масса неподвижного тела (наковальни) много больше массы движущегося тела (молота). В этом случае почти вся кинетическая энергия молота пойдет на деформацию наковки.
В самом деле, при
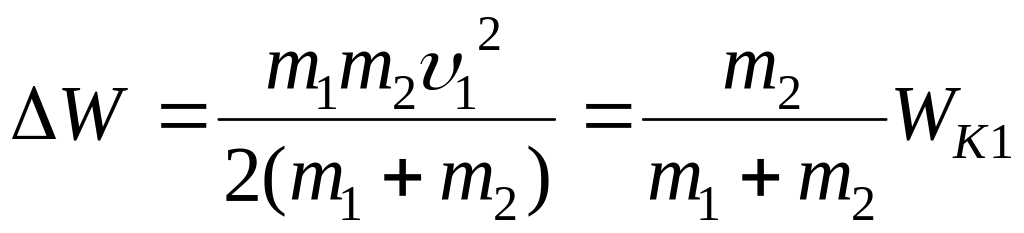 .
(11)
.
(11)
(![]() кинетическая энергия молота). Из
последнего выражения видно, что
максимальное значение
будет при
.
кинетическая энергия молота). Из
последнего выражения видно, что
максимальное значение
будет при
.
Если целью удара является перемещение
одного из тел, то расход энергии на
деформацию должен быть минимальным.
При
справедливо выражение (11), откуда следует,
что
![]() ,
если
,
если
![]() ,
то есть если
.
Следовательно, масса движущегося тела
должна быть много больше массы неподвижного
тела (молоток - гвоздь). Тогда почти вся
кинетическая энергия движущегося тела
передается неподвижному телу, и этим
обеспечивается его движение.
,
то есть если
.
Следовательно, масса движущегося тела
должна быть много больше массы неподвижного
тела (молоток - гвоздь). Тогда почти вся
кинетическая энергия движущегося тела
передается неподвижному телу, и этим
обеспечивается его движение.
