2.4 Задание2.4

Доработать схему на рисунке 3 или разработать самостоятельно для выделения постоянной и переменной составляющих.

В отчет поместить схему, расчеты и скриншоты с осциллографа

3 Резонансные цепи

3.1 Теоретические расчеты

Явление, при котором индуктивное и емкостное сопротивления в RLC-цепи (сопротивление-индуктивнсть-емкость) равны, называется резонансом.

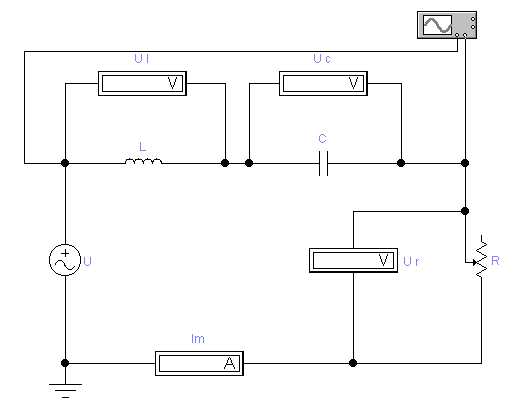
Различают последовательный (для последовательной RLC-цепи) и параллельный (для параллельной RLC-цепи) резонанс. Последовательную RLC-цепь чаще всего называют последовательным колебательным контуром (смотри рисунок 4), а параллельную RLC-цепь — параллельным колебательным контуром.

Рисунок 4 - Последовательный колебательный контур

В случае малых потерь (сопротивление R пренебрежимо мало), для обоих контуров резонанс наступает при условии, когда реактивное сопротивление цепи обращается в 0, то есть

Частота ₀ называется резонансной частотой.

Откуда получается широко известное выражение для резонансной частоты

или .

На резонансной частоте сопротивление емкости равно сопротивлению индуктивности .

Величина имеет размерность сопротивления и называется характеристическим сопротивлением контура.

Амплитуды тока и напряжений на реактивных элементах контура на резонансной частоте определяются соотношениями

I(0) = E / R,

UC (0) = UL (0) = I

Отсюда при последовательном резонансе (для последовательного контура) ток в цепи определяется только сопротивлением R и совпадает по фазе с напряжением входного сигнала.

Отношение напряжения на реактивном элементе к напряжению на контуре на резонансной частоте называется добротностью контура

Q = U_L / E = U_C / E = /R = (1/R)( ).

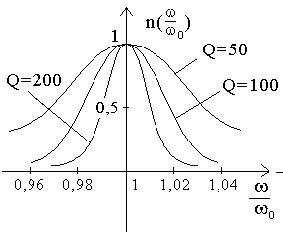
В зависимости от частотного диапазона добротность колебательных контуров на основе катушки индуктивности и конденсатора составляет Q = 20 ÷ 200 (рисунок 5).

Так как напряжение на реактивных элементах в Q раз больше входного, то говорят, что в последовательном контуре возникает резонанс напряжений (U_L = U_С = Q*E).

На практике используется также величина, обратная добротности, которая называется коэффициентом затухания d = l / Q.

Из выше приведенных формул следует, что добротность контура возрастает с увеличением индуктивности L и уменьшением сопротивления потерь R и емкости С контур

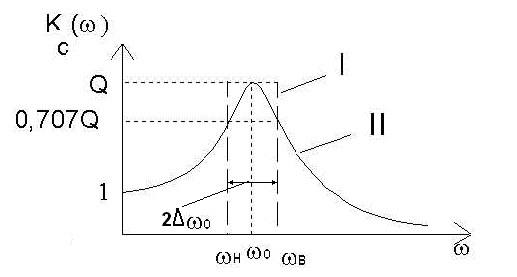
Рисунок 5 – Закон изменения амплитуды тока в контуре при изменении относительной частоты /0 (для некоторых значений добротности контура Q)	Рисунок 6 - Нормированные АЧХ:     I- идеальный, II- реальный

Важной особенностью контура является способность выделить из суммы колебаний различных частот те колебания, которые лежат вблизи резонансной частоты.

Это свойство называется частотной избирательностью. Избирательные свойства определяются формой амплитудно-частотной характеристикой (АЧХ) последовательного колебательного контура, чем ближе она к прямоугольной форме и чем уже полоса пропускания, тем выше избирательность (рисунок 6).

Полосой пропускания контура называют интервал частот, на границах которого амплитуда тока снижается до уровня 1\√2 от резонансного значения.

Полоса пропускания S  = В  - Н в идеальном случае определяется на уровне Q / √2 = 0.707 Q от максимального значения АЧХ, то есть (см. также рисунок 6)

КС(В , Н) = 0.707 KС(0) = 0.707 Q;

В = 0 (1 + 0.5 Q) , H = 0 (1 - 0.5 Q);

S = B - H = 0d =  0/Q = 2∆0

Правда, эти соотношения справедливы, когда внутреннее сопротивление генератора переменного напряжения равно нулю, а сопротивление нагрузки R = ∞ (рисунок 4).

Заметим, что с учетом внутреннего сопротивления генератора и сопротивления нагрузки R добротность контура уменьшается, полоса пропускания увеличивается, то есть уменьшается избирательность контура.

Добротность контура с учетом выше названных сопротивлений называется эквивалентной - Q_экв.

Для того чтобы Q → Q_экв, необходимо, чтобы внутреннее сопротивление генератора переменного напряжения стремилось к нулю, а сопротивление нагрузки R → ∞.