Лабораторная работа №3 Определение времени опорожнения сосуда

Цель работы: Экспериментально определить время опорожнение сосуда.

Теоретические сведения

Если емкость, из которой происходит истечение жидкости, не пополнять , то уровень жидкости в ней (напор) будет понижаться и истечение будет происходить с переменным во времени расходом.

Определим время опорожнения сосуда при переменном напоре.

За промежуток времени dt уровень жидкости в сосуде понизиться на dH (рис 3.1). Объем вытекшей за время dt жидкости равен освободившемуся в резервуаре объему, т.е.

Рис. 3.1. Истечение при переменном напоре

Определяя расход жидкости по формуле для установившегося течения , где - коэффициент расхода; - площадь сечения отверстия, получим

(3.1)

Интегрируя уравнение (3.1) по времени в пределах от нуля до времени опорожнения Т, а по высоте Н от Н₀ до нуля получаем

(3.2)

При интегрировании уравнения (3.1) делаем допущение о том, что коэффициент  расхода есть величина постоянная, хотя в действительности коэффициент расхода так же зависит от напора Н.

Подставляя формулу (3.2) зависимость площади S поперечного сечения сосуда от высоты Н и интегрируя, получим время опорожнения сосуда. Например для сосуда с постоянным по высоте поперечным сечением S время опорожнения

(3.3)

Порядок проведения работы

Порядок проведения эксперимента и схема установки (рис. 1.1) приведены в лабораторной работе №1. Определить коэффициент расхода  для отверстия или насадка, необходимо измерять площадь сечения бака S и по формуле (3.3.) рассчитать время истечения жидкости из отверстия или насадка.

Все данные занести в таблицу 3.1.

Таблица 3.1 - Результаты измерений

Тип отверстия или насадка	Диаметр отверстия d0 , м	Напор Н0 , м	Коэффициент  расхода	Время Т истечения, с

Контрольные вопросы

1. Особенности истечения жидкости из отверстия и насадка при переменном уровне жидкости в напорном баке.

2. Вычислите, какой объем жидкости вытечет из бака за время опорожнения, если в баке поддерживается постоянный напор.

3. Почему время опорожнения сосуда через насадок меньше времени опорожнения сосуда через отверстие такого же диаметра?

4. Почему время опорожнения сосуда через конический расходящийся насадок меньше, чем через сходящийся?

Лабораторная работа №4 Определение эквивалентной шероховатости трубопровода.

Цель работы: Экспериментально определить эквивалентную шероховатость трубопровода.

Теоретические сведения

При движении реальной жидкости происходит потери энергии потока, обусловленные преодолением сил трения внутри жидкости о стенки трубопровода. Потери энергии (напора) определяются из уравнения Бернулли

h_1-2 = H₁ – H₂ = z₁ – z₂ + + (4.1)

Определение удельной энергии, затрачиваемой на преодолении сил трения - одна из важнейших задач гидравлики. От потерь напора зависит выбор марки насосов, производительность самотечных трубопроводов и т. д. Потери напора нельзя определить непосредственно из уравнения Бернулли, поскольку не все составляющие в правой части уравнения (4.1) бывают известны.

Поэтому их находят суммируя потери по длине h_l и потери на местные сопротивления h_м;

h_1-2=h_l + h_м.

Потери напора по длине определяется формулой Дарси – Вейсбаха

(4.2)

где - коэффициент гидравлического сопротивления;

l, d - соответственно длинна и диаметр трубопровода, м;

w - средняя скорость движения жидкости, м/с.

Коэффициент гидравлического сопротивления - зависит от вязкости , и плотности жидкости  диаметра d, шероховатости стенок трубопровода , и средней скорости движения жидкости w.

В общем виде

(4.3)

где - число Рейнольдса;

- относительная шероховатость.

Коэффициент гидравлического сопротивления с распределением скорости по радиусу трубы соотношением

(4.4)

где w_ж - динамическая скорость.

Для ламинарного течения при параболическом профиле скоростей коэффициент гидравлического сопротивления

(4.5)

Для получения расчетных формул при турбулентном режиме течения из-за сложности происходящих при этом явлении необходимо принятие дополнительных гипотез. При наиболее распространенной гипотезе Прандтля турбулентный поток делят на ядро и вязкий ламинарный подслой (двухслойная модель течения, рис 4.1).

В ядре потока градиент скорости очень мал и весь поток движется со скоростями, близкими к средней. В ламинарном подслое градиенты скорости велики, а профиль скорости имеет параболический характер, т.е. соответствует профилю скорости при ламинарном режиме течения.

Толщина ламинарного вязкого подслоя  зависит от числа Рейнольдса. При

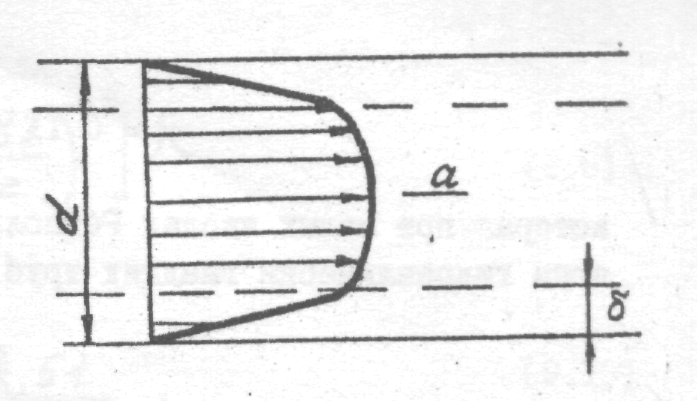
а- ядро потока; б- ламинарный подслой

Рис. 4.1. Структура турбулентного потока

относительно небольших скоростях (небольших числах Re) ламинарный подслой полностью закрывает все выступы шероховатости стенок (рис.4.2,а), в результате влияния шероховатости на потери и, следовательно, на коэффициент гидравлического сопротивления пренебрежимо малы. Эта зона турбулентного режима называется зоной гидравлически гладких труб.

Рис 4.2 - Схема ламинарного подслоя

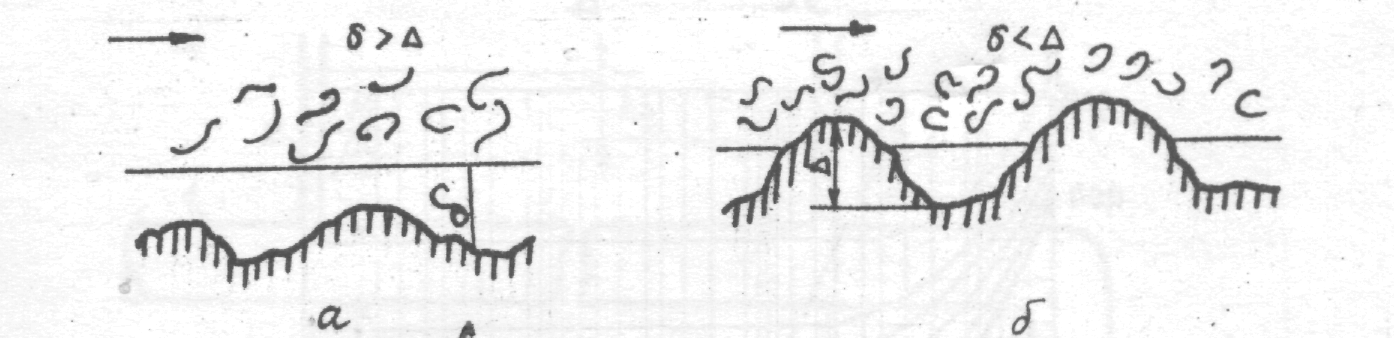
С увеличением числа Re толщина ламинарного подслоя уменьшается и влияние выступов шероховатости на потери напора увеличивается. В этой зоне (зона смешанного трения)  зависит и от Re и от

При очень больших Re ламинарный подслой становиться исчезающее мал и ядро потока захватывает практически все выступы шероховатости. В этой зоне (зона квадратичного сопротивления)  зависит только от шероховатости.

Зона смешенного трения отделяется от зоны гидравлически гладких труб кривой Re = 10 , а зона квадратичного сопротивления- кривой Re = 500 .

Многочисленными экспериментами установлено, что  зависит не только от средней высоты выступов шероховатости, но и от формы и характера их расположения на поверхности трубы. Поэтому в гидравлике вводится понятие эквивалентной шероховатости (k_э), под которой понимают не истинную высоту выступов, а такую зернистую фиктивную равномерную шероховатость, при которой потери напора равны потерям в реальном трубопроводе при тех же условиях течения.

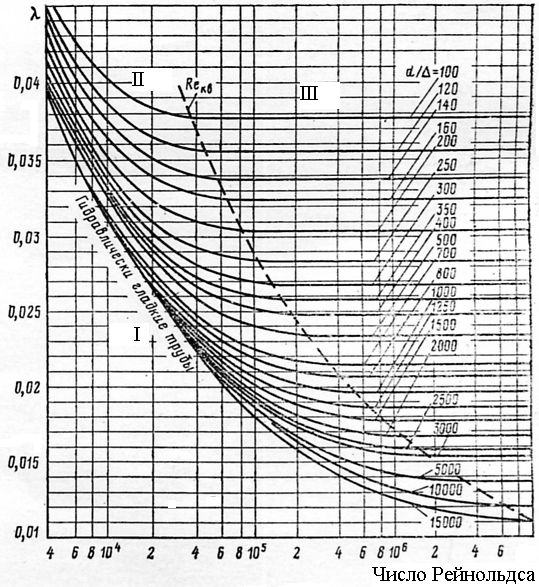График зависимости коэффициента гидравлического сопротивления от числа Рейнольдса и относительной шероховатости показан на рис. 4.3.

I- зона гидравлически гладких труб; II- переходная зона;

III – зона квадратичного сопротивления

Рис. 4.3 - Зависимость коэффициента гидравлического сопротивления

от числа Рейнольдса и относительной шероховатости

Основной расчетной формулой для определения  является полуэмпирическая формула А.Д. Альтшуля, справедливая для всей зоны турбулентного течения:

 = 0,11 (4.6)

которая при малых числах Рейнольдса переходит в формулу Блазиуса для зоны гидравлически гладких труб:

, (4.7)

а при больших числах Рейнольдса в формулу Шифринсона для зоны квадратичного сопротивления:

 = 0,11 (4.8)

Известны также формулы Н.З. Френкеля

(4.9)

и Колбрука

(4.1)

Описание установки

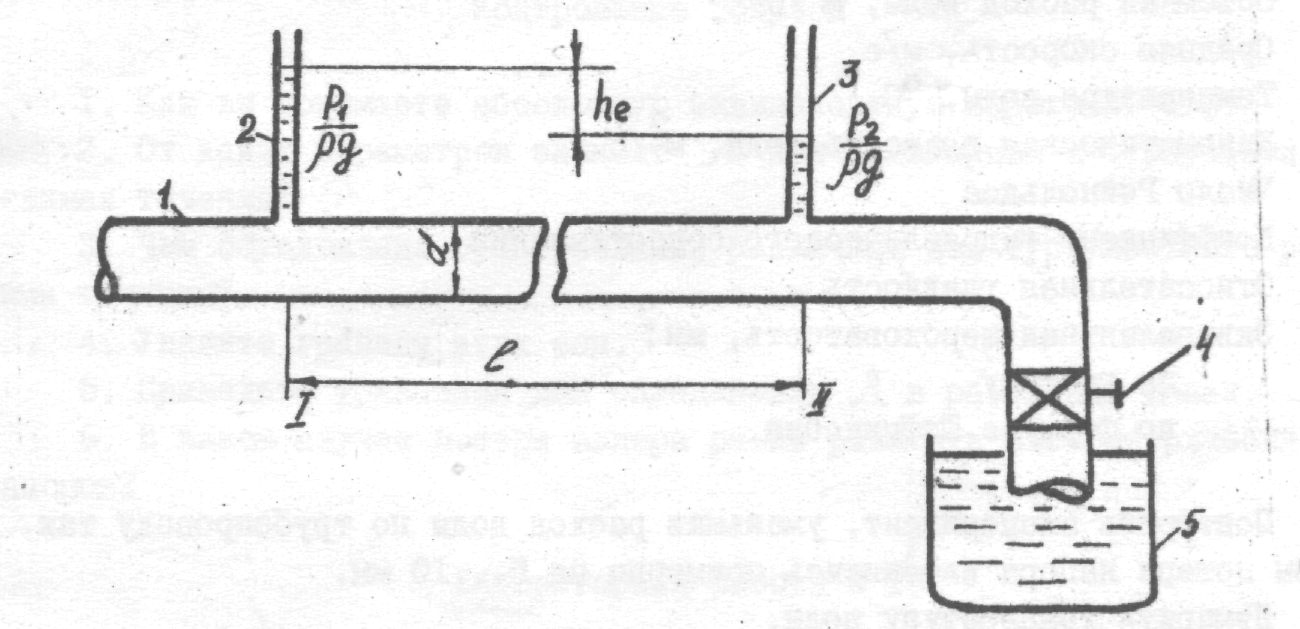
Схема установки показана на рис. 4.4. По трубопроводу 1 вода подается в мерный бак 5. В начале и в конце участка трубопровода установлены пьезометры 2 и 3, с помощью которых определяется потери напора на участке 1-2. Расход воды изменяется краном 4. Для проведения работ так же необходимо иметь секундомер и термометр.

Рис. 4.4 - Схема установки

Порядок проведения работы.

Заполнить напорный бак водой и поддерживать в баке постоянный уровень жидкости. Удалить пузырьки воздуха из трубок пьезометров и краном 4 установить минимальный расход воды.

Не менее трех раз снять показания пьезометров Н₁ и Н₂ и определить время заполнения  мерного бака 5 объемом 0,0064 м³. Данные занести в таблицу 4.1

Повторить эксперимент, уменьшив расходы воды по трубопроводу так, чтобы потери напора изменилось примерно на 5…10 мм.

Измерит температуру воды.

Обработка результатов измерения

По разности показаний пьезометров определяют потери напора h_l, по времени заполнения t мерного бака и рассчитывают расход воды (объемный способ)

Определив расход воды и диаметр трубы, найдем среднюю скорость потока:

По графику (приложение А) определяют коэффициент кинематической

вязкости воды. Рассчитывают число Рейнольдса:

Таблица 4.1 – Результаты замеров

	Величина	Значение
		1	2	3
1	Длинна участка трубы l, м
2	Диаметр трубы d, м
3	Показания пьезометров, м :
	- первого h1 =
	- второго h2 =
4	Потери напора на участке hl, м
5	Время заполнения бачка t, с
6	Объемный расход воды Q, м3/с
7	Средняя скорость w, м/с
8	Температура воды t0, 0C
9	Кинематическая вязкость воды , м2/с
10	Число Рейнольдса Re
11	Коэффициент гидравлического трения
12	Относительная гладкость d/
13	Эквивалентная шероховатость, мм:
	- по графику
	- по формуле Шифринсона

По известным Re и , используя рис. 4.3, находят относительную гладкость d/ .

По известным d/ и d определяют эквивалентную шероховатость трубы . Если полученные значения  практически одинаковы, то можно определять по формуле Шифрисона (4.8).

В расчетах использовать усредненные данные по каждому опыту.

Контрольные вопросы

1. Как вы понимаете абсолютную эквивалентную шероховатость?

2. От каких параметров зависит  при ламинарном и турбулентном режимах течения.

3. Чем обусловлено существование зон турбулентного режима течения?

4. Укажите границы этих зон.

5. Приведите уравнения для определения  в различных зонах.

6. В каком случае потери напора равны разности пьезометрических напоров?