Контрольные вопросы

1. Турбулентная фильтрация условия ее возникновения, закон турбулентной фильтрации.

2. Метод наименьших квадратов, его суть.

Лабораторная работа №9 Экспериментальное изучение свободной затопленной струи

Цель работы- экспериментально проверить зависимость осевой скорости турбулентной затопленной струи от расстояния вдоль оси для различных типов насадок.

Теоретические сведения

Струей называется поток жидкости (газа), не ограниченный какими либо твердыми поверхностями. Если струя данной жидкости (газа) движется в среде, представляющей собой ту же жидкость (газ), то такая струя считается затопленной.

Рассмотрим затопленную изометрическую струю, образовавшейся при продувании воздуха через насадку.

Вследствие турбулентного перемешивания движущихся частиц с окружающей средой, струя постепенно расширяется, что обуславливает увеличение расхода через поперечное сечение по мере удаления от места истечения и изменение скорости вдоль оси струи.

Внутри ядра струи (рис.9.1) осевая максимальная скорость не изменяется. Ядро окружено пограничным слоем, расширяющимся по мере его сужения.

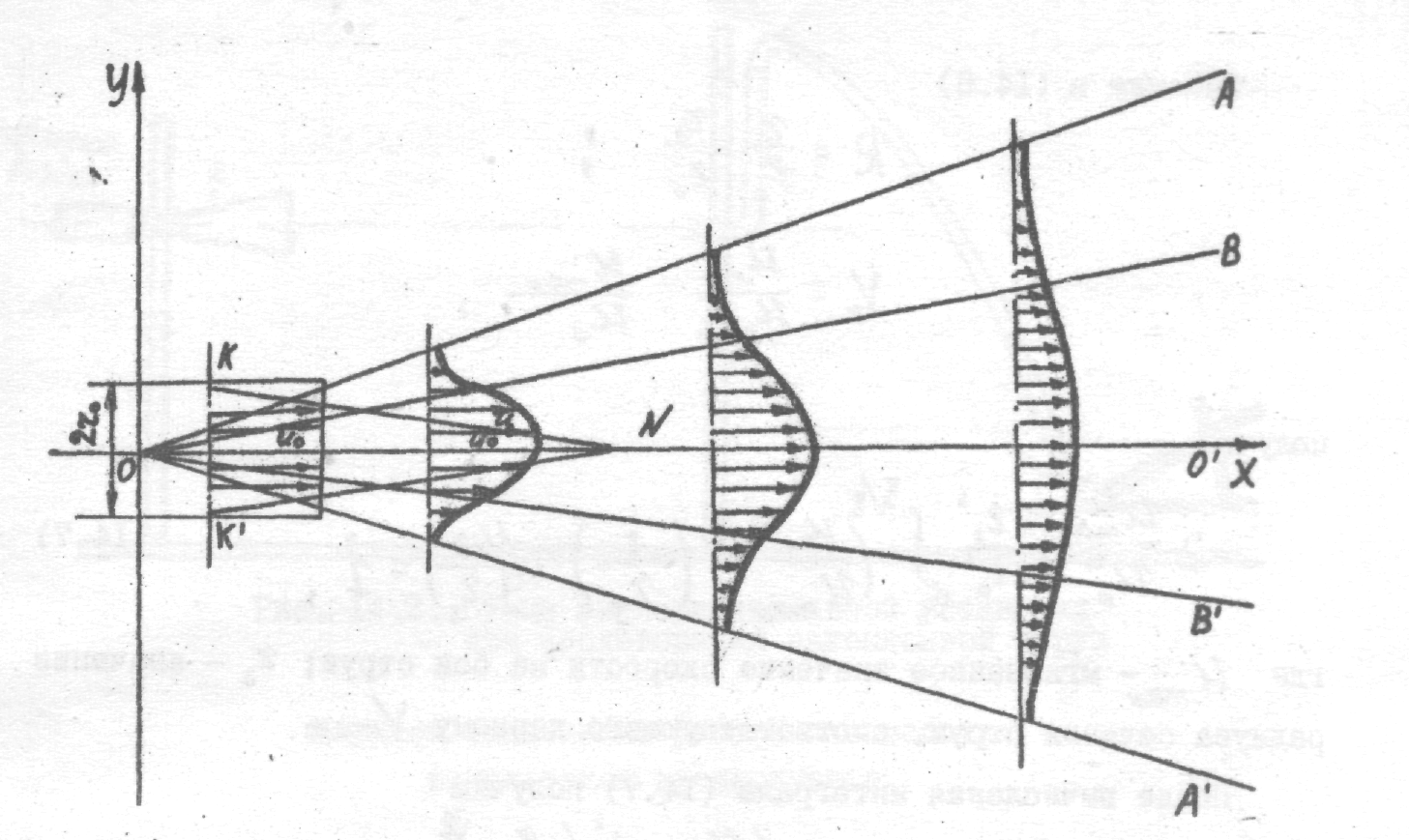
О – плюс струи; ОО^/ - ось струи; К^/К- ядро струи; ОА, ОА, ОВ, ОВ- изотахи; 2r₀- диаметр насадки; u₀- максимальная осевая скорость струи.

Рис. 9.1 - Схема течения в затопленной струе

Изотахи представляют собой линии равных относительных скоростей, т.е. в любой точке на них выполняется равенство:

, (9.1)

где w- средняя скорость струи вдоль оси ОХ.

Точка пресечение изотах – это полюс струи.

Полагая статическое давление в струе равным давлению в окружающей неподвижной среде, применим закон сохранения импульса для произвольного сечения  струи с сечением насадки ₀:

, (9.2)

где m  масса жидкости (газа) протекающая через произвольное сечение струи;

u_x – скорость струи вдоль оси ОХ;

d_m- масса элементарной струйки в произвольном сечении, протекающая за 1 с;

m₀- масса жидкости (газа), протекающая через сечение насадки;

u₀- начальная скорость струи.

Учтем, что

(9.3)

После подстановки (9.3) в (9.2) получим:

(9.4)

Если затопленная струя вытекает из круглого отверстия радиуса r₀, то уравнение (9.4) приобретает вид

, (9.5)

где r_s- радиус произвольного сечения струи .

Введем безразмерные переменные и V_x= и перепишем уравнение (9.5) в виде

(9.6)

Заменим в (9.6)

;

Получим

(9.7)

где u_max- мгновенное значение скорости на оси струи;

r_s- значение радиуса сечения струи, соответствующему данному V_max.

После вычисления интеграла (9.7) получим

откуда с достаточной точностью приближения, учитывая, что , где - угол между осью и границей распространения струи.

Значение постоянной можно определить опытным путем, чем и проверить правильность теоретических выкладок.