Матрица коэффициентов параметрических уравнений поправок (матрица в)
|
Сухое |
Высокое |
|||||||
|
δZ1 |
δZ2 |
δZ3 |
δZ4 |
δZ5 |
ζ4 |
η4 |
ζ5 |
η5 |
М1-2 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
М1-5 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
-0,603 |
-0,025 |
М2-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
М2-5 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
-0,105 |
0,375 |
М2-4 |
0 |
-1 |
0 |
0 |
0 |
-0,336 |
0,180 |
0 |
0 |
М2-3 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
М3-2 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
М3-4 |
0 |
0 |
-1 |
0 |
0 |
0,029 |
0,382 |
0 |
0 |
М4-3 |
0 |
0 |
0 |
-1 |
0 |
0,029 |
0,382 |
0 |
0 |
М4-2 |
0 |
0 |
0 |
-1 |
0 |
-0,336 |
0,180 |
0 |
0 |
М4-5 |
0 |
0 |
0 |
-1 |
0 |
-0,392 |
-0,297 |
0,392 |
0,297 |
М5-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
-0,603 |
-0,025 |
М5-4 |
0 |
0 |
0 |
0 |
-1 |
-0,392 |
-0,297 |
0,392 |
0,297 |
М5-2 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
-0,105 |
0,375 |
Установление единицы веса и вычисление исходной весовой матрицы p для уравниваемых величин
Измеряемые углы на пунктах триангуляции представляются рядом равноточных независимых направлений. Поэтому в качестве единицы веса взят вес измерения направлений. Корреляционная матрица ошибок направлений и ее весовая матрица PМ будут равны единичной матрице:
Q = PМ = Е.
Вычисление корреляционной матрицы
ошибок координат определяемых пунктов
Корреляционная матрица ошибок необходимых параметров равна обратной матрице коэффициентов нормальных уравнений:
В результате вычислений получим:
Матрица Qt
0,7105 |
0,0842 |
-0,0424 |
0,0387 |
0,2327 |
-0,4865 |
-0,1851 |
-0,7126 |
0,3513 |
0,0842 |
0,4167 |
0,0845 |
0,2515 |
0,2513 |
-0,7253 |
0,4974 |
-0,3124 |
0,8016 |
-0,0424 |
0,0845 |
0,6499 |
0,1763 |
0,0112 |
-0,2376 |
0,8027 |
0,1266 |
0,3385 |
0,0387 |
0,2515 |
0,1763 |
0,815 |
0,2907 |
-1,3887 |
1,0286 |
-0,1655 |
0,8979 |
0,2327 |
0,2513 |
0,0112 |
0,2907 |
0,8551 |
-1,0492 |
0,1385 |
-0,8317 |
1,4412 |
-0,4865 |
-0,7253 |
-0,2376 |
-1,3887 |
-1,0492 |
5,6764 |
-1,6748 |
1,6706 |
-1,3785 |
-0,1851 |
0,4974 |
0,8027 |
1,0286 |
0,1385 |
-1,6748 |
4,3298 |
0,5361 |
1,8769 |
-0,7126 |
-0,3124 |
0,1266 |
-0,1655 |
-0,8317 |
1,6706 |
0,5361 |
2,4223 |
-1,4148 |
0,3513 |
0,8016 |
0,3385 |
0,8979 |
1,4412 |
-1,3785 |
1,8769 |
-1,4148 |
6,018 |
матрицу
можно
разбить на блоки
где
—
корреляционная матрица ошибок уравненных
значений
ориентирующих углов:
Матрица
0,7105 |
0,0842 |
-0,0424 |
0,0387 |
0,2327 |
0,0842 |
0,4167 |
0,0845 |
0,2515 |
0,2513 |
-0,0424 |
0,0845 |
0,6499 |
0,1763 |
0,0112 |
0,0387 |
0,2515 |
0,1763 |
0,815 |
0,2907 |
—
матрица
взаимных весовых коэффициентов между
уравненными значениями ориентирующих углов и уравненными значениями
координат определяемых пунктов:
Матрица
-
-0,4865
-0,7253
-0,2376
-1,3887
-1,0492
-0,1851
0,4974
0,8027
1,0286
0,1385
-0,7126
-0,3124
0,1266
-0,1655
-0,8317
0,3513
0,8016
-0,8317
0,8979
1,4412
—
корреляционная
матрица ошибок координат определяемых
пунктов:
Матрица
-
-1,0492
5,6764
-1,6748
1,6706
-1,3785
0,1385
-1,6748
4,3298
0,5361
1,8769
-0,8317
1,6706
0,5361
2,4223
-1,4148
1,4412
-1,3785
1,8769
-1,4148
6,018
Вычисление корреляционных матриц
ошибок дирекционных углов и длин сторон сети
Дирекционные углы и длины сторон геодезической сети являются функциями координат
Корреляционные матрицы их ошибок в уравненной сети вычисляются по формулам:
F — матрица частных производных оцениваемых дирекционных углов;
Fs — матрица частных производных оцениваемых длин сторон сети.
Известно, что
,
,
,
где
и
—
модельные значения дирекционных углов
и длин сторон проектируемой сети.
Производные
,
,
и
равны
,
,
.
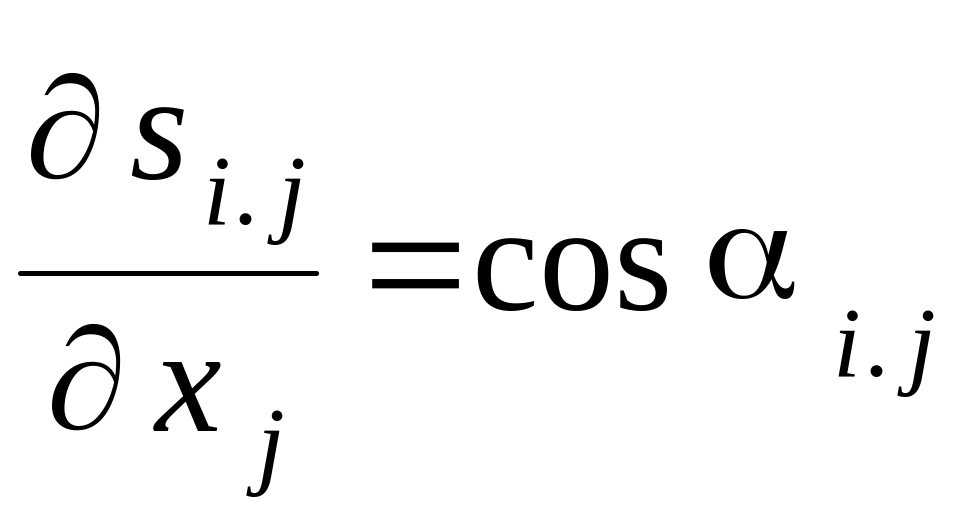Значения производных оцениваемых функций представляют собой матрицы F и Fs соответственно