Контрольные вопросы

1. В чем заключается физический смысл момента инерции? От чего зависит момент инерции?

2. В чем сущность метода крутильных колебаний?

3. Какие параметры влияют на период колебаний крутильного маятника?

4. Почему Т и Т₀ много больше Т_р?

5. Как рассчитать J₀?

6. Почему у параллелепипеда J_x  J_y  J_z,, а у куба J_x = J_y = J_z?

Работа 5. Определение момента инерции с помощью маятника Обербека

Цель работы – исследовать зависимость момента инерции крестовины с грузами от распределения массы относительно оси вращения, проходящей через центр масс.

Общие сведения

Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении (см. рисунок). Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок.

К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести и сила натяжения , поэтому на основании второго закона Ньютона можно записать

(1)

где g – ускорение свободного падения; а – ускорение, с которым движется груз.

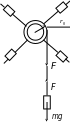
Крестовина приходит во вращательное движение под действием момента силы натяжения

; = Fr₀, (2)

где J – момент инерции относительно оси вращения;  – угловое ускорение; r₀ – радиус шкива.

Из уравнений (1) и (2) получим

. (3)

Так как угловое ускорение связано с ускорением а соотношением  = а/r₀, то формула (3) принимает вид

, (4)

где а = 2h/t²; h – путь, пройденный грузом за время t.

Таким образом, с учетом формулы (4) получим

. (5)

Порядок выполнения работы

1. Убедиться, что две неподвижные рамки установлены на вертикальной линейке на расстоянии 40-50 см друг от друга. Измерить радиус шкива r₀.

2. Установить грузы на стержнях на максимальном расстоянии от оси вращения и закрепить их.

3. Включить установку, нажав кнопку «ПУСК».

4. Не отпуская кнопку «ПУСК» нажать кнопку «СБРОС» и намотать нить на шкив, установив подвешенный груз на уровне верхней рамки выше оптической оси фотоэлектрического датчика.

5. Закрепить груз, нажав кнопку «ПУСК» и обнулить счетчик нажатием кнопки «СБРОС».

6. Опустить груз, отключив электромагнит нажатием кнопки «ПУСК», измерить время t его движения до оптической оси нижней рамки. Взять не менее трех отсчетов t и вычислить .

7. Сместить грузы на стержнях на два деления к центру и повторить пп.4-6, измерить расстояние r от оси вращения до центра масс груза.

8. Повторить измерения для 8-10 положений грузов.

9. Записать результаты экспериментов в табличной форме:

Номер опыта	r	t		Jэ	Jр
1
2
…

Экспериментальные значения момента инерции J_э рассчитать по формуле (5).

10. Обработать результаты измерений. Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой , если считать грузы материальными точками, можно выразить формулой

(6)

где J₀ – момент инерции крестовины без грузов.

Из формулы (6) следует, что J = f(r²). Следовательно, если построить график этой функции, то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей J₀. Такое построение можно сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдений позволяют сделать такое построение достаточно точным. Легче всего сделать это с помощью метода наименьших квадратов. Суть этого метода состоит в том, что из всех возможных прямых линий надо взять такую, для которой сумма квадратов отклонений каждой точки от прямой будет наименьшей.

Для удобства перепишем формулу (6) в виде

, (7)

где r² = х и  = K. Согласно методу

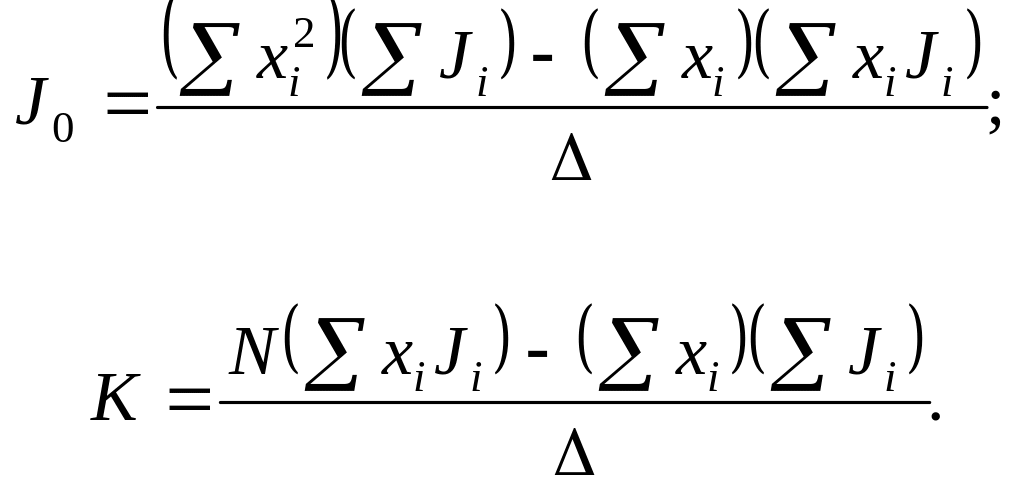(8)

где ; N – число опытов; J_i – экспериментальное значение момента инерции J_э, полученное для каждого опыта.

Обработку результатов эксперимента удобно вести в табличной форме:

Номер опыта		ri	xi	Ji		xiJi
1
2
…

Рассчитав J₀ и K по формулам (8), следует построить зависимость J_р от x по формуле (7). Так как через две точки можно провести только одну прямую, то для построения этой прямой можно взять какие-нибудь две удобные точки. Далее по формуле (7) рассчитать момент инерции J_p для каждого опыта, заполняя последний столбец (см. п.9).

Среднее квадратическое отклонение

.

11. По данным опыта и расчетов построить график функции в координатах J – r², предварительно обработав данные опыта методом наименьших квадратов, и вычислить доверительный интервал измерения момента инерции в границах .