Министерство образования Российской Федерации

Омский государственный технический университет

Моделирование

Электромеханических переходных

Процессов на эвм

Методические указания к лабораторным работам

Омск-2001

Составители: Шкаруба Михаил Васильевич, канд. техн. наук,

доц. каф. «Электроснабжение промышленных предприятий»;

Эрнст Александр Дмитриевич, канд. техн. наук,

доц. каф. «Электроснабжение промышленных предприятий».

Методические указания “Моделирование электромеханических переходных процессов на ЭВМ” являются продолжением методических указаний, изданных в 2000 году.

Общие теоретические положения к лабораторным работам № 3-5

Асинхронные двигатели обычно составляют основную часть нагрузки электрических систем и оказывают непосредственное влияние на устойчивую работу всей системы. В определенных условиях работа самих двигателей оказывается неустойчивой. Так, при значительном снижении напряжения на выводах двигателей происходит их опрокидывание и они останавливаются.

В лабораторных работах исследуется устойчивость асинхронной нагрузки. Исследования проводятся для общей схемы, изображенной на рис.1, в которой асинхронный двигатель мощностью Р_d вращает производственный механизм с тормозным моментом мощностью P_T и питается от независимого источника, имеющего э.д.с. Е, через реактивное сопротивление х_С.

При изучении режимов работы асинхронного двигателя на ЭВМ двигатель представляется схемой замещения. Реальные физические процессы, происходящие в двигателях, хорошо отражаются Т-образной схемой замещения [8], приведенной на рис. 2. Здесь введены следующие обозначения: r₁ и x₁ – активное и индуктивное сопротивления статора; и – приведенные активное и индуктивное сопротивления ротора; r_ и x_ -активное и индуктивное сопротивления намагничивающей цепи; I₁ и I_ - токи статора и намагничивающей цепи; –приведенный ток ротора; s- скольжение или относительная разность скоростей вращения поля ₀ и ротора  (s= ).

Параметры схемы замещения можно определить по паспортным данным двигателя [6].

Параметры намагничивающей цепи можно найти из следующих соображений. Магнитный поток при изменении скольжения от s0 до s_н практически не изменяется, поэтому ток I_ можно оценить по номинальному режиму [6].

,

где cos_н и s_н –номинальные значения косинуса и скольжения; I_н – номинальный ток двигателя; s_кр – критическое скольжение, соответствующее максимальному моменту М_max на валу двигателя. Ток I_н определяется по формуле

,

где _н – номинальный к.п.д., о.е.; Р_н – номинальная мощность, Вт; U_н – номинальное напряжение, В.

Критическое скольжение

, (1)

где - кратность максимального момента двигателя; М _н – номинальный момент; M _max – максимальный момент.

Активным сопротивлением цепи намагничивания можно пренебречь, так как

r_ << x_ [6] , и тогда индуктивное сопротивление этой цепи

. (2)

Активное сопротивление статора r₁ можно принять равным приведенному активному сопротивлению ротора s0 [6]:

(3)

где Р_мех – механические потери (в лабораторных работах Р_мех0,01Р_н );

с₁-коэффициент приведения цепи ротора.

Приведенное активное сопротивление фазы ротора при s=1 [6]

где - кратность пускового момента М_п двигателя; к_п - кратность пускового тока I_п двигателя, к_п= .

Приведенное активное сопротивление фазы ротора из-за вытеснения тока зависит от скольжения и изменяется от до .

Поэтому для произвольного s сопротивление r^₂ нужно определять по формуле [6]

.

При выполнении заданий к лабораторным работам нужно определять для s_н:

. (4)

Приведенное индуктивное сопротивление рассеяния ротора из-за вытеснения тока также зависит от скольжения и изменяется от до _.

В [6] рекомендуется при s>0,05 о.е. (s> 5 %) вычислять по формуле

, (5)

а в диапазоне от s0 до s=5 % (s=0,05 о.е.) принять постоянным и равным сопротивлению при s=0,05 о.е.

.

При выполнении заданий к лабораторным работам №3-5 сопротивление нужно вычислять для s_н ( ).

Для определения и необходимо найти суммарное индуктивное сопротивление рассеяния двигателя x_s для граничных случаев. Для s=1 его можно определить (если пренебречь намагничивающим током) по формуле [6]

, (6)

где z_d1- полное сопротивление двигателя при неподвижном роторе.

(7)

Для s0 суммарное индуктивное сопротивление рассеяния двигателя [6]

= , (8)

где с₁ – коэффициент преобразования.

Решая совместно (6) и (8) , находим, что

и . (9)

Однако для изучения переходных процессов более удобной является

Г-образная схема замещения (рис. 3а), в которой намагничивающая цепь вынесена к месту приложения напряжения U_d. Для перехода от Т-образной схемы к Г-об-разной необходимо вычислить коэффициент преобразования [8]

, (10)

где z₁-полное сопротивление статора; z_- полное сопротивление цепи намагничивания. В лабораторных работах с₁ следует принять равным 1,03.

При изучении статической устойчивости асинхронной нагрузки Г-образная схема замещения обычно упрощается [2]. В схеме не учитываются: коэффициент преобразования с₁, в намагничивающей цепи – потери (r₀=0) и сопротивление х_1, а в цепи рассеяния обмоток - потери в обмотке статора (r₁=0) . В цепи намагничивания остается только индуктивное сопротивление х_ (рис. 3б). Для цепи рассеяния обмоток (для удобства написания формул) введем обозначения x_S и r_S , где x_S равно сумме индуктивных сопротивлений обмоток ( ), а r_S –приведенному активному сопротивлению ротора ( ). Изменением сопротивлений и из-за вытеснения тока ротора с ростом скольжения пренебрегают и считают их постоянными (в лабораторных работах №3 и №4 они вычисляются при s_н). Эти упрощения существенно не изменяют полного сопротивления двигателя, но позволяют наглядно показать влияние скольжения s на устойчивость нагрузки (в лабораторной работе №5 при исследовании динамической устойчивости нагрузки влияние скольжения на сопротивления и учитывается).

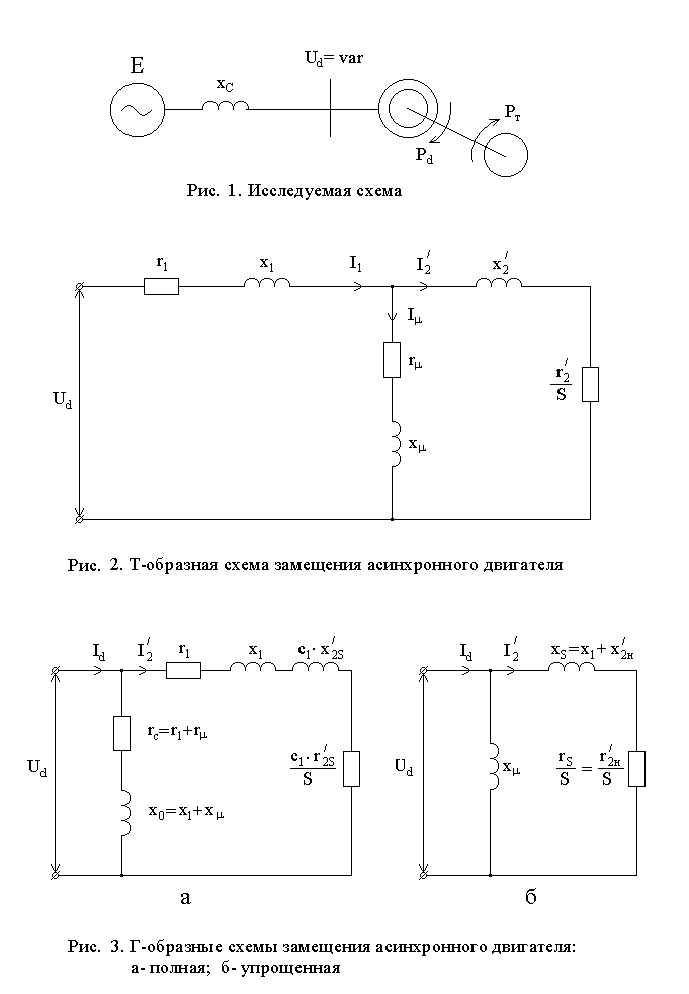
Устойчивость асинхронного двигателя обычно определяют по характеристикам электромагнитной мощности двигателя P_d=f(s) и мощности тормозного момента производственного механизма P_т=f(s) (рис. 4). Характеристики имеют две точки пересечения а и б, причем в точке а режим устойчивый, так как при возмущении с ростом скольжения s растет и ускоряющая избыточная мощность двигателя, поэтому скорость двигателя начинает возрастать, скольжение - уменьшаться и первоначальный режим восстанавливается. А в точке б возникает тормозящая избыточная мощность, скольжение продолжает расти и двигатель останавливается. Точка а будет рабочей точкой двигателя, которой соответствует мощность Р₀ и скольжение s₀.

Если напряжение на шинах снижается, то уменьшается максимальная мощность двигателя P_max и рабочая точка смещается в сторону увеличения скольжения. Область устойчивой работы асинхронного двигателя при снижении напряжения на двигателе зависит от вида характеристики мощности тормозного момента P_T =f (s).

Если характеристика P_T = const, то критерий устойчивости двигателя имеет вид

, (11)

т.е. предельным режимом, с точки зрения устойчивости, является точка s_кр, где характеристика P_d =f (s) достигает максимального значения.

Если характеристика мощности тормозного момента P_T =f (s) имеет падающий характер, то критерием статической устойчивости двигателя является положительный знак избыточной мощности (dP=dP_d-dP_т) при увеличении скольжения s , т.е. условие [4]

. (12)

В этом случае характеристика P_T =f (s) имеет отрицательную производную и устойчивая работа двигателя возможна в некоторой области за максимумом функции P_d =f (s) при . На рис. 5 приведены характеристики асинхронного двигателя и нагрузки для предельного случая. При снижении напряжения на двигателе до U_пред обе характеристики будут иметь только одну общую точку при скольжении s_пред , которое лежит в диапазоне 1> s_пред> s_кр .

В курсах “ Электрические машины ” и “ Электропривод ” для асинхронных двигателей обычно строят механические характеристики моментов, а не мощностей ( M_d =f (s) и M_T = f (s)) .

В лабораторных работах также исследуются характеристики моментов, только построенные в относительных единицах ( m_d =f (s) и m_T = f (s) ).

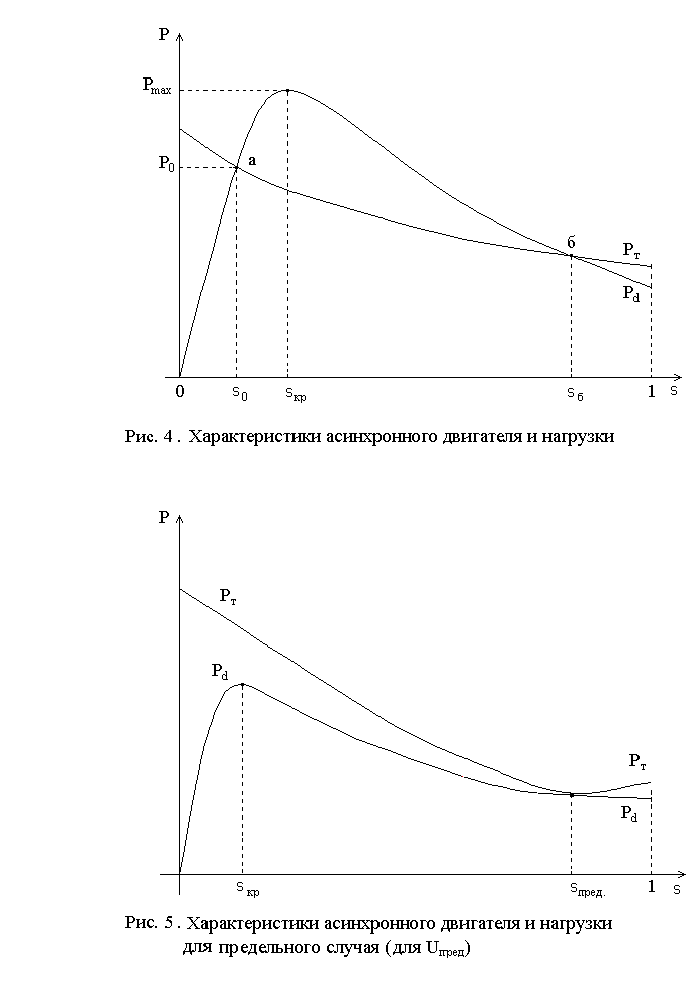
На рис. 6 приведены два вида механических характеристик момента сопротивления нагрузки, построенных в относительных единицах [5]:

а) m_T = const ;

б) m_T = m_тр + (к_З – m_тр)(1-s)^ , (13)

где m_тр – начальный момент трения при s=1; к_З - коэффициент загрузки двигателя ( ); - показатель степени, характеризующий механизм.

Показатель  принимает значения от 0 до 3. Характеристики с постоянным моментом сопротивления (=0) имеют транспортеры, шаровые мельницы; линейную зависимость (=1) имеет система двигатель-генератор; показатель =2 – у вентиляторов, насосов, а в некоторых случаях показатель степени может дости-

гать =3.

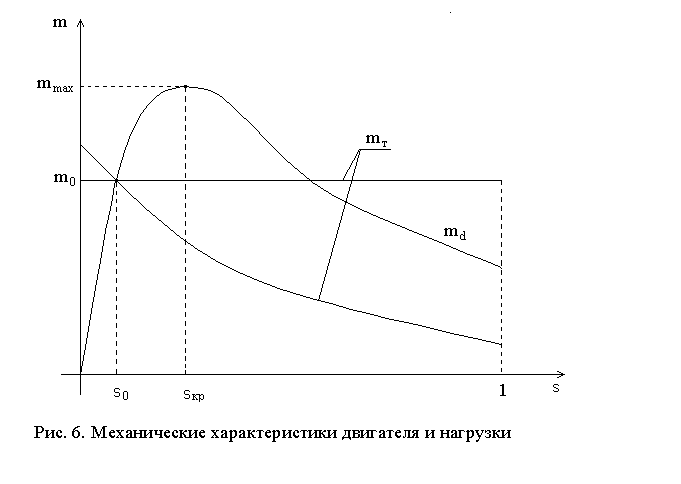
Механическую характеристику асинхронного двигателя в относительных единицах с достаточной для практических расчетов точностью можно построить по формуле [6]

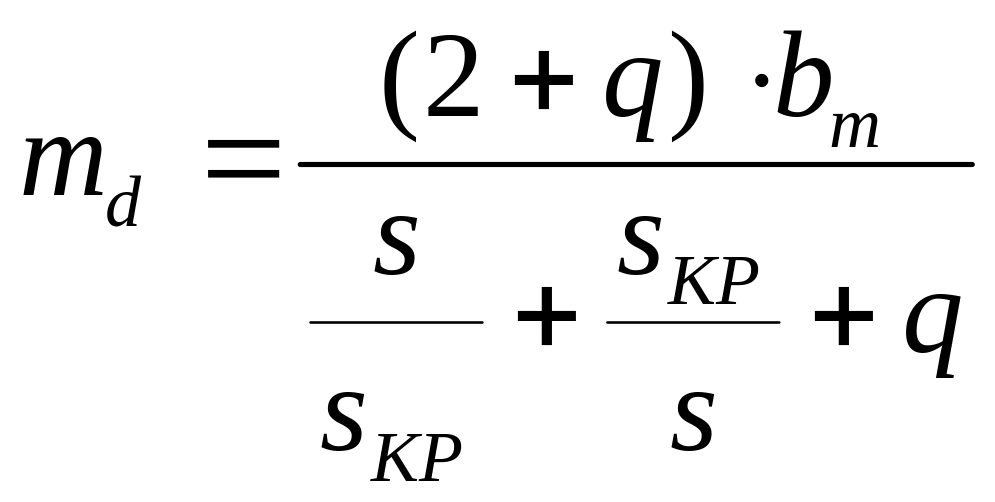, (14)

где q-параметр, он определяется по формуле

.

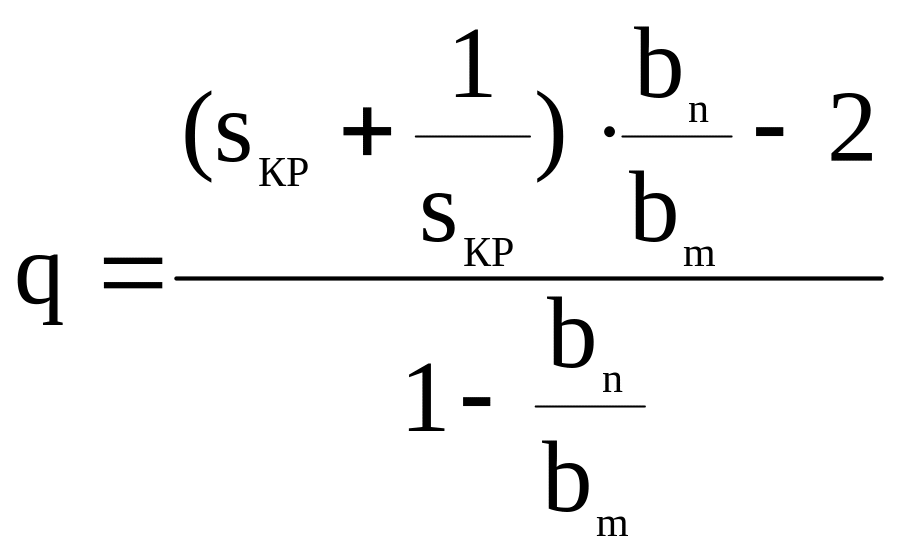Причем при s<s_кр следует принять q=0 и формула (14) преобразуется в формулу Клосса [5]:

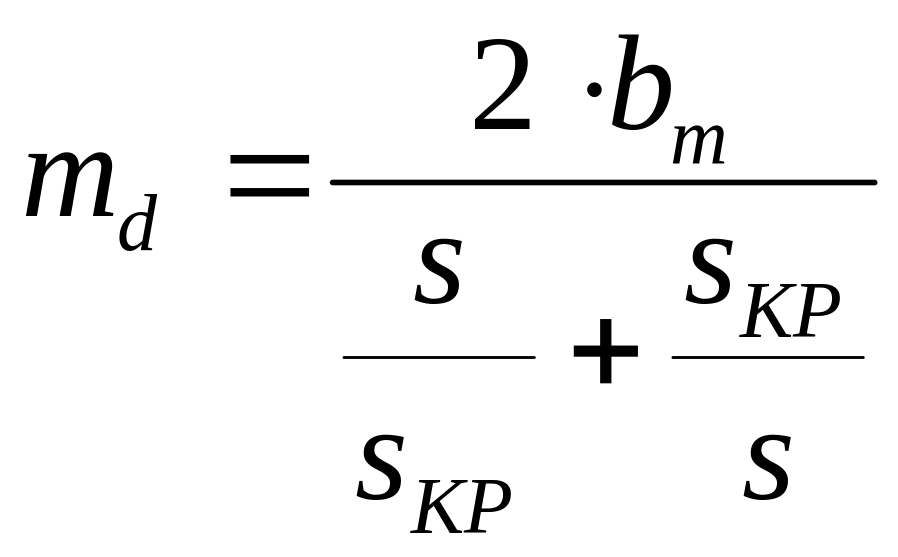. (15)

При снижении напряжения на двигателе U_d механическая характеристика двигателя принимает вид [5]

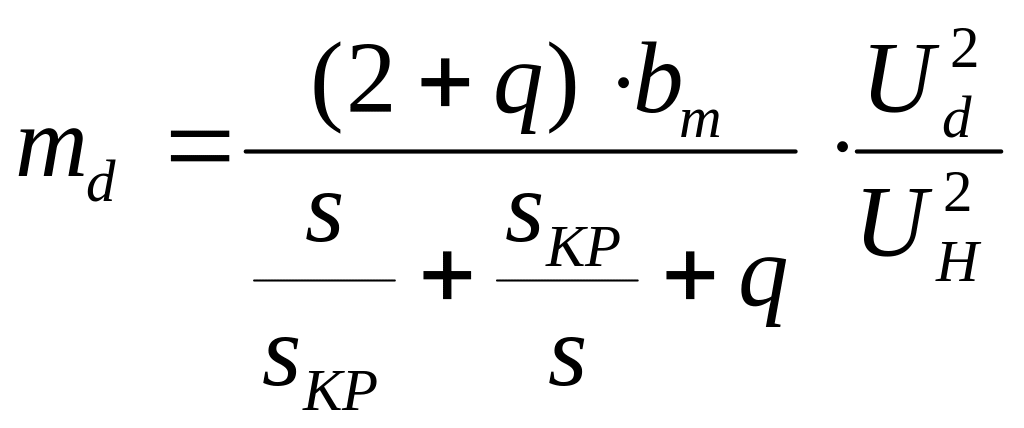. (16)

Паспортные данные исследуемых двигателей [7], исходные данные моментов сопротивления производственных механизмов (нагрузок двигателей) и питающих систем приведены в табл.1-3.

Таблица 1

Паспортные данные исследуемых двигателей

№ варианта	1	2	3	4	5	6	7	8
Рн , кВт	7,5	90	160	400	630	1250	2500	5000
Uн , кВ	0,38	0,38	0,38	6	6	6	6	6
nн, об/мин	970	985	985	1484	1484	2973	2973	2973
cosН , о.е.	0,81	0,89	0,9	0,88	0,88	0,89	0,89	0,9
Sн , %	3,2	1,8	1,4	1,35	1,3	0,7	0,9	0,6
bmax=Mmax/Mн, о.е.	2,5	2,2	2,2	2,1	2,3	2,1	2	2,2
bп=Mn/Mн , о.е.	2	1,2	1,4	1,0	1,2	0,95	0,95	0,9
kп=In/Iн , о.е.	6	7	7	5,1	5,7	5,5	5	5,7
н , %	85,5	92,5	93,5	93,7	95,1	96,3	97	97,5
Jd , кгм2	0,058	3,4	7,3	10	12	13	24	56

№ варианта	9	10	11	12	13	14	15	16
Рн , кВт	15	30	55	110	800	1600	2000	4000
Uн , кВ	0,38	0,38	0,38	0,38	6	6	6	6
nн, об/мин	975	980	985	985	2970	2973	2973	2973
cosН , о.е	0,87	0,9	0,89	0,9	0,92	0,89	0,89	0,89
Sн , %	2,6	2,3	1,3	2	0,7	0,9	0,9	0,89
bmax=Mmax/Mн, о.е.	2	2	2,1	2,1	2,1	2,0	2,0	2,0
bп=Mn/Mн , о.е	1,2	1,2	1,2	1,2	1,2	0,9	0,95	0,95
kп=In/Iн , о.е.	6	6,5	6,5	7,0	5,2	5,2	5,1	5,1
н , %	87,5	90,5	91,5	93,0	95,6	96,5	97,2	97,0
Jd , кгм2	0,18	0,45	1,26	4,5	12,5	14	18	40

Таблица 2

Исходные данные моментов сопротивления механизмов

№ варианта	1	2	3	4	5	6	7	8
mтр , о.е.	0,5	0,4	0,5	0,4	0,45	0,3	0,4	0,3
кз , о.е.	0,95	0,92	0,9	0,9	0,98	0,85	0,9	0,8
 , о.е.	2	2	3	2	3	3	2	3
JМ , кгм2	0,1	4,5	8,0	10	13	15	25	60

№ варианта	9	10	11	12	13	14	15	16
mтр , о.е.	0,5	0,45	0,5	0,5	0,5	0,3	0,4	0,4
кз , о.е.	0,95	0,92	0,95	0,95	0,98	0,85	0,9	0,9
 , о.е.	2	2	3	2	3	3	2	2
JМ , кгм2	0,25	0,65	2	5,3	13,5	16	20	44

Таблица 3

Исходные параметры системы

№ варианта	1	2	3	4	5	6	7	8
E/Uн , о.е.	1,05	1,03	1,04	1,05	1,05	1,06	1,04	1,04

№ варианта	9	10	11	12	13	14	15	16
E/Uн , о.е.	1,05	1,04	1,03	1,05	1,05	1,06	1,04	1,04