
Лабораторная работа № 2 исследование динамической устойчивости электропередачи
Цель работы: Исследование динамической устойчивости электропередачи на ЭВМ и определение предельного времени отключения трехфазного короткого замыкания.
Динамическая устойчивость – это способность системы восстанавли-вать после большого возмущения исходное состояние или состояние, прак-тически близкое к исходному (допустимому по условиям эксплуатации) [2].
Исследование
динамической устойчивости проведем
для простейшей электрической системы
[1] (рис. 6а), состоящей из генератора Г,
работаю-щего через трансформатор
Тр
и двухцепную линию
![]() и
и
![]() на шины
сис-темы С
бесконечной мощности (
на шины
сис-темы С
бесконечной мощности (![]() )
в случае металлического трех-фазного
короткого замыкания в начале линии
(точка K
). Генератор
при-водится в движение турбиной Т
мощностью РТ
.
)
в случае металлического трех-фазного
короткого замыкания в начале линии
(точка K
). Генератор
при-водится в движение турбиной Т
мощностью РТ
.

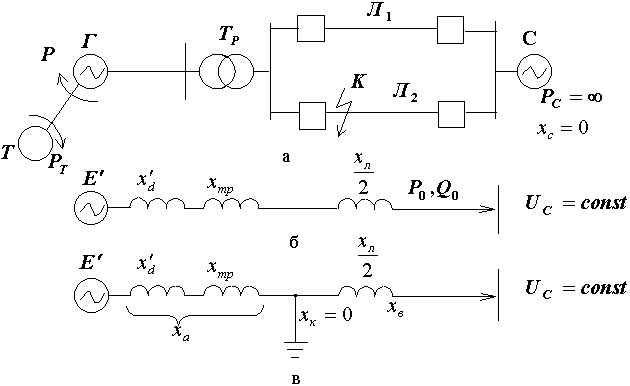
Рис. 6. Исследуемая система: а – электрическая схема; б – схема замещения
доаварийного режима; в – схема замещения аварийного режима.
Линия
через время
![]() после возникновения короткого замыкания
отключается защитой линии. Электромеханический
переходный процесс, вы-званный таким
возмущением исходного режима, может
развиваться двояко: либо он заканчивается
установлением нового режима, близкого
к нормаль-ному (режим динамически
устойчив), либо нормальный режим
становится невозможным (режим динамически
неустойчив).
после возникновения короткого замыкания
отключается защитой линии. Электромеханический
переходный процесс, вы-званный таким
возмущением исходного режима, может
развиваться двояко: либо он заканчивается
установлением нового режима, близкого
к нормаль-ному (режим динамически
устойчив), либо нормальный режим
становится невозможным (режим динамически
неустойчив).
Векторная диаграмма,
приведенная на рис. 2, справедлива и для
этой системы. Здесь только вместо
сопротивления электропередачи
![]() исполь-зуется
сопротивление электропередачи до
короткого замыкания
исполь-зуется
сопротивление электропередачи до
короткого замыкания
![]() или сопротивление электропередачи
после отключения короткого замыкания
или сопротивление электропередачи
после отключения короткого замыкания
![]() .
.
![]() (16)
(16)
![]() (17)
(17)
О динамической
устойчивости электропередачи можно
судить по зависи-мости
![]() ,
где
,
где
![]() угол между векторами э.д.с.
угол между векторами э.д.с.
![]() и напряжением на шинах системы
и напряжением на шинах системы
![]() .
.
Переходные процессы при больших возмущениях обычно анализируют
упрощенно, делая ряд допущений [3].
При изучении рассматриваемого случая сделаны следующие допущения.
Во–первых, активная электрическая мощность при переходе от одного режима к другому изменяется мгновенно, хотя это не должно происходить мгновенно, так как связано с изменением запаса механической и электро-магнитной энергии в отдельных элементах.
Во–вторых, принято,
что потокосцепление обмотки возбуждения
во время переходного процесса неизменно,
т. е. э.д.с.
![]() .
Для упро-щения
анализа устойчивости э.д.с.
.
Для упро-щения
анализа устойчивости э.д.с.
![]() можно принять равной
можно принять равной
![]() (см. рис. 2) которую легко определить по
формуле (4).
(см. рис. 2) которую легко определить по
формуле (4).
Угловая характеристика мощности имеет вид
![]()
В
этом случае, вместо угла
(между
и
![]() )
стоит угол
)
стоит угол
![]() (между
(между
![]() и
см. рис.2), однако он имеет такой же
характер изменения и по зави-симости
и
см. рис.2), однако он имеет такой же
характер изменения и по зави-симости
![]() тоже можно судить о динамической
устойчивости элек-тропередачи.
тоже можно судить о динамической
устойчивости элек-тропередачи.
Характер динамической
устойчивости электропередачи зависит
от то-го, насколько быстро ликвидирован
аварийный режим. В лабораторной работе
необходимо определить предельное по
условию динамической устой-чивости
электропередачи время отключения
короткого замыкания
![]() ,
после которого устойчивая работа
электропередачи уже невозможна. Зна-чение
в лабораторной работе определяется
подбором по зависимостям
,
после которого устойчивая работа
электропередачи уже невозможна. Зна-чение
в лабораторной работе определяется
подбором по зависимостям
![]() и
и
![]() .
Необходимо найти такое максимальное
время
.
Необходимо найти такое максимальное
время
![]() ,
при котором зависимости
и
остаются еще затухаю-щими.
,
при котором зависимости
и
остаются еще затухаю-щими.
Чтобы облегчить
эту задачу, значение
перед началом подбора нужно оценить.
Это можно сделать, если по правилу
площадей [2] опреде-лить предельный угол
отключения короткого замыкания
![]() ,
а затем подставить его в частный случай
решения дифференциального уравнения
движения ротора.
,
а затем подставить его в частный случай
решения дифференциального уравнения
движения ротора.
Правило площадей записывается на основе закона сохранения и превращения энергии. Согласно этому закону в исследуемом случае во всех относительных перемещениях ротора сумма кинетической и потенциальной энергии остается неизменной.
В общем виде правило площадей формулируется так [2]:
![]() .
.
Для исследуемого критического случая получим (рис. 7):
![]() ,
,
где
![]() - площадка ускорения.
- площадка ускорения.
 ,
,
она
вычисляется от начального угла
![]() до предельного угла отключения
до предельного угла отключения
![]() ,
соответствующего предельному времени
,
соответствующего предельному времени
![]() ;
;
![]() - площадка возможного
торможения.
- площадка возможного
торможения.
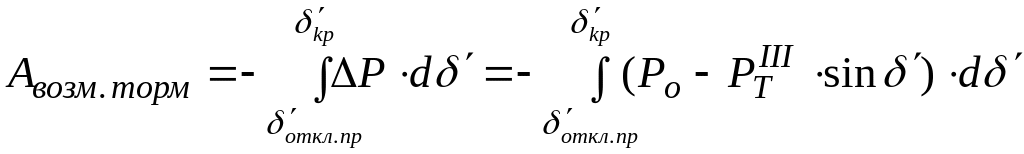 ,
,
она
вычисляется от
![]() до критического значения угла
до критического значения угла
![]() ,
при котором
,
при котором
![]() .
.
Для того чтобы
воспользоваться этим правилом, нужно
построить угло-вые характеристики
мощности
![]() для трех режимов.
для трех режимов.
Доаварийный режим:
![]() (18)
(18)
Режим
характеризуется углом между векторами
![]() и
и
![]()
 (19)
(19)
Аварийный режим:
![]() .
.
Схема
замещения электропередачи для этого
случая приведена на рис. 6в, откуда
следует, что при
![]()
![]()
![]() .
.
Послеаварийный режим:
![]() .
(20)
.
(20)
Послеаварийный
режим принципиально возможен, если
![]() .
.
Он характеризуется углом
 .
(21)
.
(21)
Для предельного случая отключения короткого замыкания площадка ускорения равна площадке возможного торможения (рис.7), т.е.
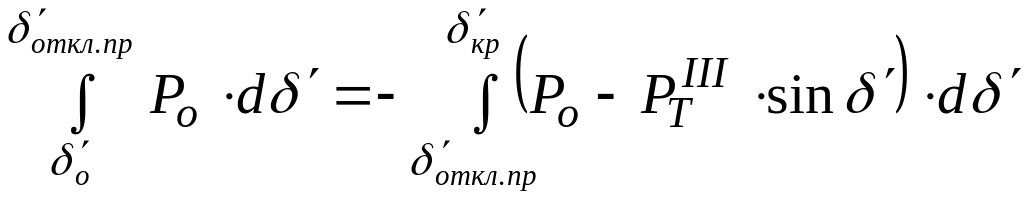 .
.
Отсюда находим предельный угол отклонения короткого замыкания
 ,
(22)
,
(22)
где
![]() .
.
По углу можно оценить предельное время отключения , если найти частный случай решения дифференциального уравнения движения ротора (25). При трехфазном коротком замыкании и отсутствии демп-фирования дифференциальное уравнение имеет вид
![]() ,
,
где
![]() -
постоянная инерция ротора, о. е.;
-
постоянная инерция ротора, о. е.;
![]() - мощность турбины, о. е.
- мощность турбины, о. е.
Это уравнение имеет решение
![]() .
(23)
.
(23)
Из
формулы (23), приняв
![]() ,
оценим предельное значение времени
короткого замыкания
,
оценим предельное значение времени
короткого замыкания
 .
(24)
.
(24)
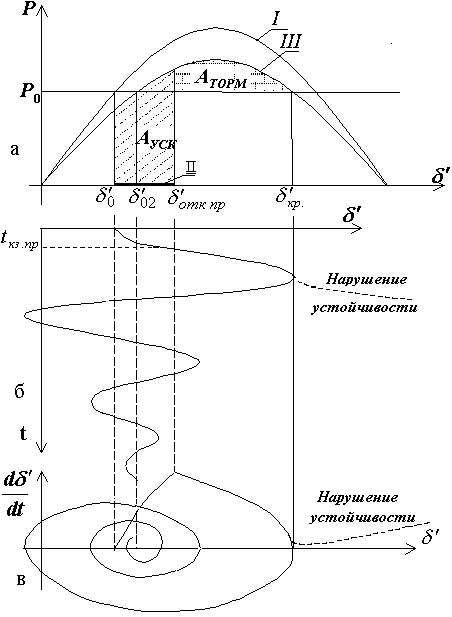
Рис. 7. Предельный случай при нарушении динамической устойчивости
системы:
а – угловые характеристики мощности для трех режи-
мов; б - возможные изменения угла во времени; в – характерис-
тики ускорения .
Для того чтобы по
этой формуле получить время в секундах,
углы нужно подставлять в радианах,
мощность
![]() в относительных единицах, а постоянную
инерции
в относительных единицах, а постоянную
инерции
![]() - в секундах в квадрате на радиан
- в секундах в квадрате на радиан
![]() ,
где
,
где
![]() в о. е.
в о. е.
Однако
расчетное
![]() ,
полученное по формуле (24), меньше
,
полученное по формуле (24), меньше
![]() на 5 – 15%, так как правило площадей не
учитывает демпфирование переходного
процес-са.
на 5 – 15%, так как правило площадей не
учитывает демпфирование переходного
процес-са.
Для построения зависимости (после отключения короткого замыкания) в лабораторной работе решается дифференциальное уравнение движения ротора для общего случая [4]:
![]() ,
(25)
,
(25)
где
- постоянная инерции ротора;
- мощность турбины;
![]() - мощность генератора;
- мощность генератора;
![]() - коэффициент демпфирования, с помощью
которого учиты-вается действие регулятора
скорости турбины или регулятора
возбуждения, реагирующих на изменение
скорости
- коэффициент демпфирования, с помощью
которого учиты-вается действие регулятора
скорости турбины или регулятора
возбуждения, реагирующих на изменение
скорости
![]() .
.
Это уравнение решается методом Эйлера в интервале от до 5 се-кунд. Для того чтобы время получилось в секундах, углы следует подстав-лять в радианах, мощность – в относительных единицах, коэффициент демп-фирования – в секундах на радиан, а постоянную инерции – в секундах в квадрате на радиан.
Для времени от 0
до
полное сопротивление цепи
![]() ,
поэтому мощность генератора
,
поэтому мощность генератора
![]() и дифференциальное уравнение упрощается:
и дифференциальное уравнение упрощается:
![]() .
.
На рис. 7б показана
зависимость
.
При
![]() происходит ко-роткое замыкание и угол
начинает увеличиваться. При
короткое замы-кание отключается (в
предельном случае при
и угле
),
но угол по инерции продолжает увеличиваться
(в предельном случае до
),
а затем уменьшается, и после ряда
колебаний устанавливается новое значение
угла
происходит ко-роткое замыкание и угол
начинает увеличиваться. При
короткое замы-кание отключается (в
предельном случае при
и угле
),
но угол по инерции продолжает увеличиваться
(в предельном случае до
),
а затем уменьшается, и после ряда
колебаний устанавливается новое значение
угла
![]() .
Если режим неустойчивый, то угол
увеличивается неограниченно.
.
Если режим неустойчивый, то угол
увеличивается неограниченно.
На этом же рисунке
показана зависимость
,
которая для случая
![]() имеет форму закручивающейся спирали.
имеет форму закручивающейся спирали.
По
этим зависимостям подбором и определяется
значение предельного вре-мени короткого
замыкания
.
Для облегчения подбора на экран выво-дятся
угловые характеристики мощности
,
вычисленные значения площадок ускорения
и торможения
![]() ,
а так же превышение пло-щадки
над площадкой ускорения
,
а так же превышение пло-щадки
над площадкой ускорения
![]() :
:
![]() .
.
Значение
![]() помогает ускорить подбор
,
так как позволяет численно оценить
разницу между введенными
и
(при этом следует помнить, что метод
площадок занижает значение
на 5 – 15%).
помогает ускорить подбор
,
так как позволяет численно оценить
разницу между введенными
и
(при этом следует помнить, что метод
площадок занижает значение
на 5 – 15%).
