5.5. Формула ньютона - лейбніца

Теорема 3. Якщо функція неперервна на відрізку a, b і F(x) - одна з її первісних, то обчислення визначеного інтеґрала функції по відрізку можна здійснити за допомогою так званої формули Ньютона¹-Лейбніца²

. ( 23 )

■ Ми маємо дві первісні для функції , а саме: названу первісну і, крім того, визначений інтеґрал (формула (21)) з змінною верхньою ме-жею x. За відповідною властивістю первісної різниця функцій і є сталою, тобто

.

Щоб знайти значння сталої C, покладімо . Матимемо

,

і тому

.

Замінюючи x на b і t на x, отримуємо формулу (23).■

Зауваження. Вираз

,

який означає дію , називається подвійною підстановкою.

Приклад 6. Обчислити визначений інтеґрал

Первісною для є , і за формулою Ньютона-Лейбніца

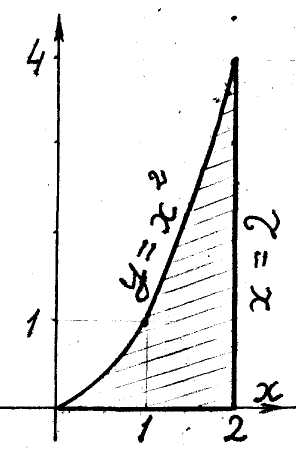
Приклад 7. Знайти площу фігури, обмеженої наступними лініями: , (рис. 5).

Задана фігура є криволінійною трапецією, і за форму-лою (10) її площа дорівнює визначеному інтеґралу від функ- Рис. 5 ції по відрізку ,

.

Приклад 8. Частинка рухається вздовж прямої, і її швидкість через t с після проходження точки O дорівнює м/с. Знайти відстань частинки від точки O через 2 с, а також середнє значення її швидкості протягом проміжку часу від до .

Згідно з формулою (12) шукана відстань дорівнює

м.

Використовуючи далі формулу (20) і результат щойно проведеного інтеґ-рування, маємо

.

Приклад 9. Знайти середнє значення функції на відрізку .

За формулою (20)

.

5.6. Основні методи обчислення визначеного інтеґрала

5.6.1. Заміна змінної (спосіб підстановки)

Теорема 4. Нехай: 1) функція неперервна на відрізку [a, b]; 2) функ-ція неперервна зі своєю похідною на відрізку [α, β]; 3) виконуються рівності , . Тоді має місце наступна формула (формула заміни змінної)

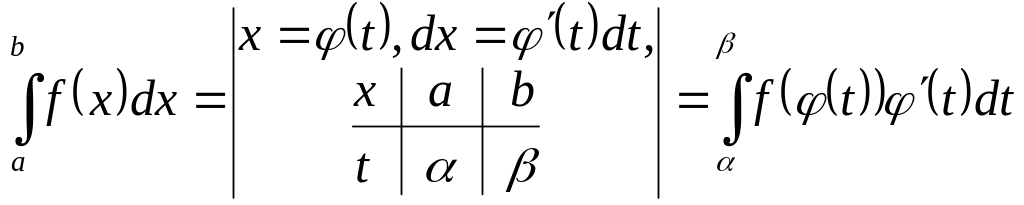. ( 24 )

■ Нехай - якась первісна функції . Тоді є первісною функції . За формулою Ньютона-Лейбніца

а) інтеґрал ліворуч дорівнює

;

б) інтеґрал праворуч має таке ж саме значення, оскільки

.■

Зауваження. На відміну від невизначеного інтеґрала післе застосування формули (24) не треба повертатися до попередньої змінної інтеґрування.

Приклад 10. Обчислити визначений інтеґрал

.

Покладімо . Тоді , так що

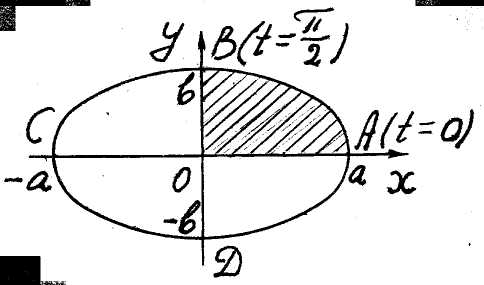
Приклад 11. Знайти площу фігури, обмеженої еліпсом

(рис. 6). Рис. 6 Достатньо знайти почетверену площу частини OAB фігури.

Перший спосіб. З рівняння еліпса

,

і тому

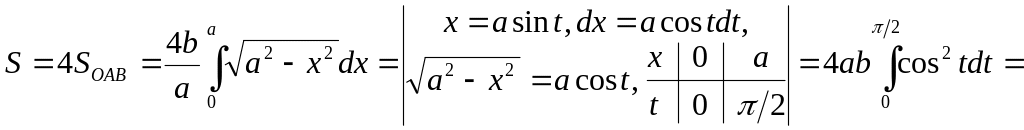
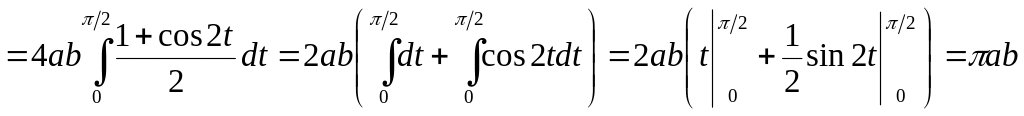
Другий спосіб. Краще перейти до параметричних рівнянь еліпса, а саме: . В цьому випадку заміна змінної в результаті якої ми повинні взяти , дає той же результат значно простіше,

.

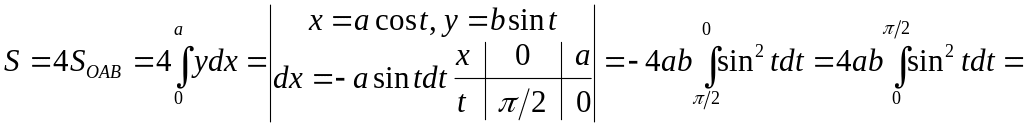
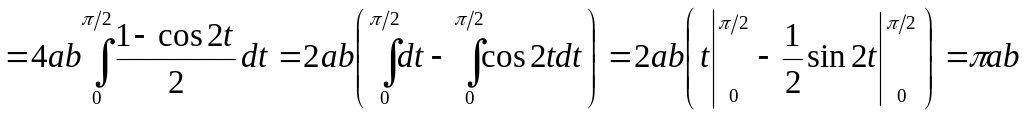5.6.2. Інтеґрування частинами

Теорема 5. Якщо функції неперервні з своїми похідними на відрізку , то справедливою є наступна формула (формула інтеґрування частинами):

( 25 )

■Для доведення формули достатньо проінтеґруровати від a до b обидві частини рівності

і застосувати формулу Ньютона-Лейбніца для інтеґрала від функції .■

Приклад 12. Обчислити визначений інтеґрал

.

Використовуючи інтеґрування частинами, отримуємо

.

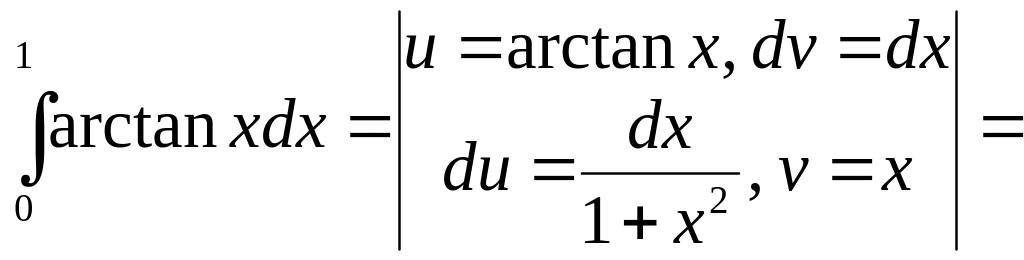
Приклад 13. Обчислити площу фігу-ри, обмеженої двома лініями (див. рис. 7). Рис. 7 Лінії перетинаються в точках і утворюють фігуру (рис. 7). Її площа дорівнює різниці площ двох криволінійних трапецій . Тому

.

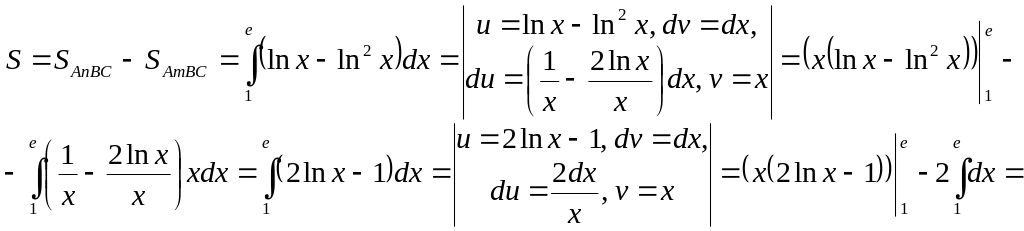
Приклад 14. Нехай

.

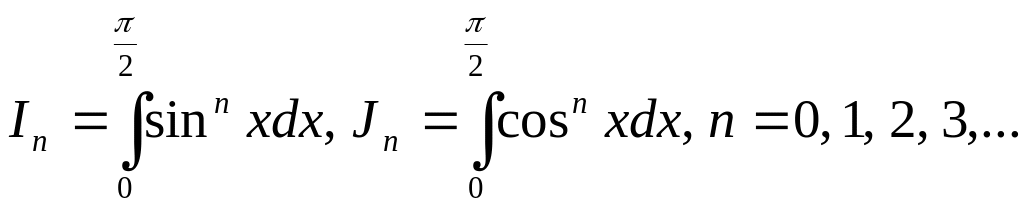Довести, що

.

■

■

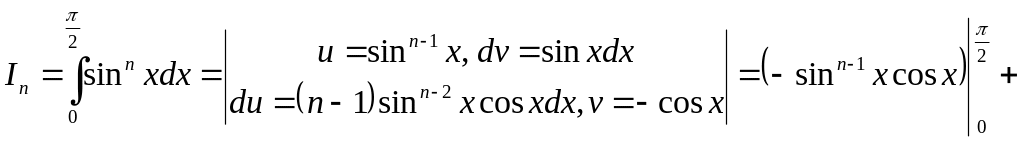
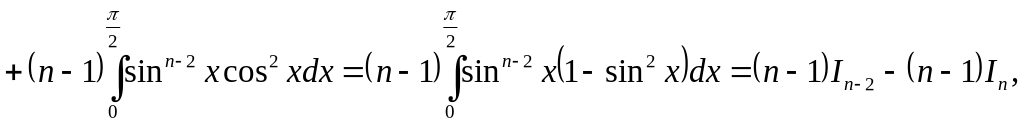
Наприклад,

.

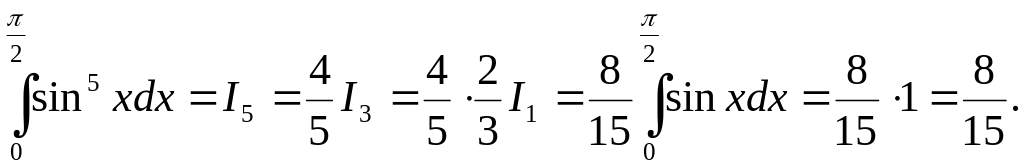
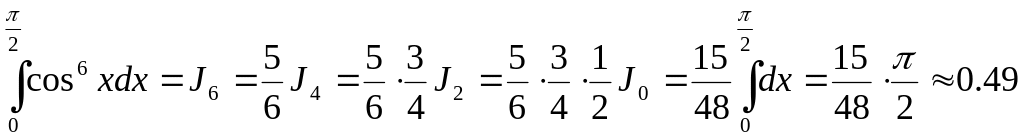Приклад 15. Знайти залишковий член формули Тейлора в формі Ла-ґранжа.

Нехай, наприклад, , і

.

За формулою Лаґранжа . Взявши

,

маємо

,

і після інтеґрування по відрізку отримуємо

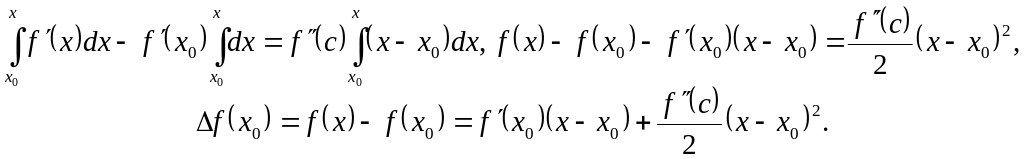Таким чином,

Щоб знайти для довільного n ми пишемо

потім покладаємо , і за формулою Лаґранжа маємо

.

Далі ми n раз інтеґруємо по відрізку і отримуємо

…

тобто