5.3. Властивості визначеного інтеґрала

5.3.1. Лінійність та адитивність

1 (однорідність). Сталий множник k може бути винесений за знак визначеного інтеґрала,

.

■Утворимо інтеґральні суми для лівої и правої частин. Вони рівні, оскільки

.

Тому їх границі, тобто відповідні визначені інтеґрали, є також рівними.■

2 (адитивність відносно підінтеґральної функції). Якщо - дві інтеґровні функції, то

.

Доведіть цю властивість самостійно.

Наслідок (лінійність). Для будь-яких двох інтеґровних функцій і довільних сталих

.

3 (адитивність відносно інтервалу інтеґрування). Для будь-яких a, b, c

,

якщо принаймні два з трьох інтеґралів існують.

■1) Нехай спочатку c(a, b). Утворимо інтеґральну суму так, щоб c було точкою ділення. В такому випадку (позначення зрозумілі)

,

і перехід до границі при доводить властивість.

2) Нехай тепер розташування точок a, b, c довільне, наприклад, . Застосовуючи перший випадок до інтервала і означення 5, отримаємо

звідки

.■

5 .3.2. Інтеґрування нерівностей. Теорема про середнє

4. Якщо a < b і підінтеґральна функція невід"ємна на відрізку , , то

.

Інтеґрал строго додатний, якщо функція неперервна на відрізку і не дорівнює нулю тотожно.

■ Невід"ємність інтеґрала безпосередньо випливає з додатності інтеґраль-ної суми для функції Його строга додатність, як можна довести більш складними міркуваннями, є результатом неперервності функції. ■

5. Якщо a < b і на , то

.

Інтеґрали пов"язані строгою нерівністю, якщо функції неперервні на відрізку і не рівні тотожно.

■Достатньо застосувати попередню властивість до різниці .■

Приклад 2.

,

оскільки на відрізку .

6. Якщо a < b, то

( 17 )

■ Достатньо застосувати властивість 5 до подвійної нерівності

■

7 (двобічна оцінка визначеного інтеґрала). Якщо a < b і функція неперервна на відрізку a, b, то справедливою є подвійна нерівність

. ( 18 )

■Доведення випливає з властивості 5, нерівності на та формули (13).■

Приклад 3. Оцінити інтеґрал

.

Маємо

і на підставі формули (18)

.

8. Теорема про середнє. Якщо функція непнрервна на відрізку , то існує точка така, що

( 19 )

Рис. 3 ■Нехай, наприклад, a < b. Діленням обох частин не-рівності (18) на додатне число отримуємо

.

Згідно з теоремою Больцано¹–Коші для функції, яка неперервна на відрізку , існує точка така, що

.

Випадок розглядається таким же чином. Зробіть це самостійно.■

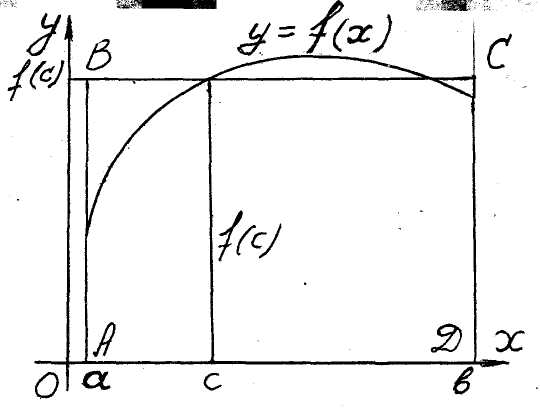
Геометричний сенс теореми про середнє (рис. 3). Площа криволінійної трапеції (1) дорівнює площі прямокутника ABCD з тією ж основою AD=a, b і висотою .

Означення 6. Вираз

( 20 )

називається середнім значенням функції на відрізку a, b.

5.4. Визначений інтеґрал як функція своєї верхньої межі

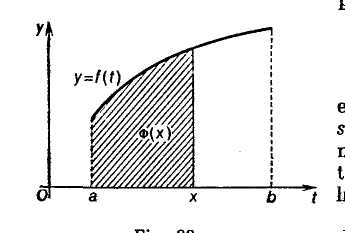Нехай xa, b. Розглядемо функцію

, ( 21 )

тобто визначений інтеґрал с змінною верхньою межею x. Геометрично (для невід"ємної підінтеґ- Рис. 4 ральної функції ) цей інтеґрал дає площу тієї частини криволінійної трапеції

,

яка лежить між прямими (рис. 4).

Теорема 2. Якщо функція неперервна на відрезку a, b, то для будь-якого похідна інтеґрала (21) дорівнює

, ( 22 )

тобто похідна визначеного інтеґрала з змінною верхнью межею x по цій межі дорівнює значенню підінтеґральної функції в точці x.

■За означенням похідної

.

Використовуючи адитивність визначеного інтеґрала відносно інтервалу інтеґрування, маємо

Нехай, наприклад, . На підставі теореми про середнє існує така точка в інтервалі , що

.

При цьому , якщо . Беручи до уваги неперервність функції f, ми дістаємо

.■

Наслідок (основна теорема інтеґрального числення). Кожна функція, неперервна на відрізку a, b, має первісну на a, b.

■Однією з таких первісних є інтеґрал (21) з змінною верхньою межею x.■

Приклад 4. Знайти похідну функції

.

Згідно з формулою (22)

.

Приклад 5. Знайти похідну функції

.

Використовуючи властивість адитивності визначеного інтеґрала відносно інтервалу інтеґрування, правило диференціювання складеної функції та формулу (22), отримуємо
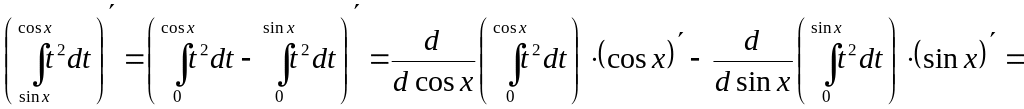