8.4. Гама-функція ейлера

Означення 8. Гама-функцією (або - функцією) Ейлера називається таких невласний інтеґрал

( 18 )

В повних курсах математичного аналізу доводиться, що -функція неперервна зі всіма своїми похідними для будь-якого .

Відзначимо деякі властивості -функції.

1) .

■ .■

2) .

■

■

3) Для натуральних значень властивість 2 набуває вигляду

■

■

Означення 8.

Згідно ж цим означенням -функція є поширенням на множину всіх додатних дійсних чисел відомої факториіал-функції

,

визначеної на множині всіх натуральних чисел.

Приклад.

■На підставі означення 8 маємо ■

9. Подвійний інтеґрал

9.1. Подвійний інтеґрал та його властивості

Означення 1. Нехай функцію двох змінних задано в деякій області D площини (рис. 1).

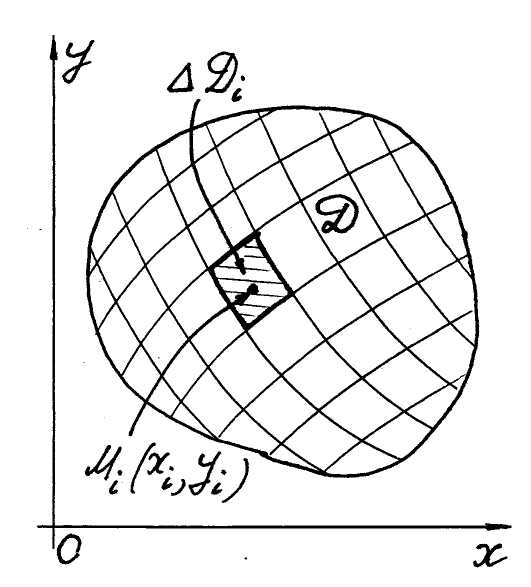1. Поділимо область на n частин з площами і діаметрами .

2. Візьмемо довільну точку в кожній частині , знайдемо значення функцаї в цій точці та помножимо його на площу цієї частини .

3. Додамо всі отримані добутки Рис. 1

і отримаємо інтеґральну суму (інтеґральну суму Коші-Рімана)

.

4. Нехай і . Якщо існує границя інтеґральної суми , то він називається подвійним інтеґралом функції по області D і позначається

( 1 )

Ми можемо трактувати подвійний інтеґрал як суму елементів , де dS = dxdy – елемент площі.

Теорема 1 (існування подвійного інтеґрала). Якщо підінтеґральна функція неперервна в області D, то подвійний інтеґрал по ній існує.

Очевидно, що для випадку подвійний інтеґрал дає площу області D,

. ( 2 )

Механічний сенс подвійного інтеґрала. Якщо - поверхня густина пластинки , то її маса дорівнює подвійному інтеґралу

( 3 )

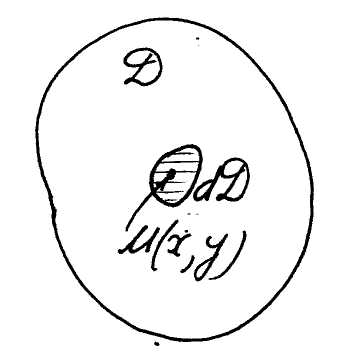
■Елемент маси

є масою елементу з площею і сталою поверхне-вою густиною (рис. 2). Сума всіх цих елементів дає масу пластинки, зображену подвійним Рис. 2 інтеґралом (3).■

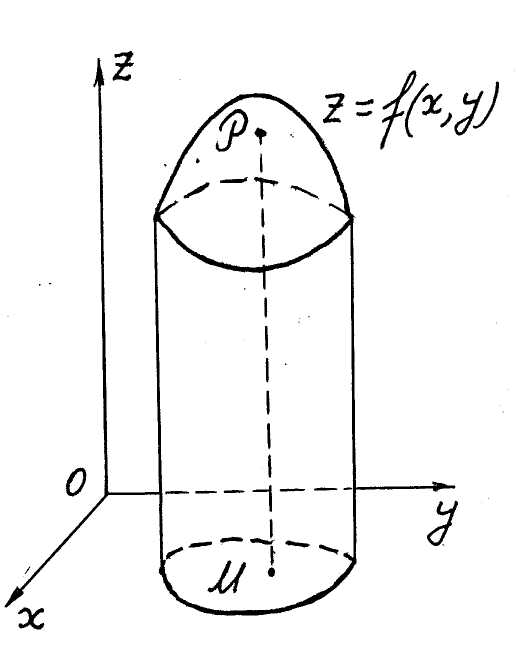
Означення 2. Циліндричним тілом [криволінійним циліндром] называє-ться тіло, обмежене:

a) зверху – поверхнею

;

b) знизу - областю D площини xOy;

c) збоку – циліндричною поверх- нею з твірною, паралельною до осі , і Рис. 3 Рис. 4 напрямною, яка є границею області D (див. рис. 3).

Геометричний сенс подвійного інтеґрала. Об"єм циліндричного тіла дорівнює подвійному інтеґралу

. ( 4 )

■Елемент об"єму

є об"єм прямого циліндра з основою площі і висотою

(рис. 4).

Об"єм циліндричного тіла дорівнює сумі всіх таких елементів і дається подвійним інтеґралом (4).■

Властивості подвійного інтеґрала аналогічні влас-тивостям визначеного інтеґрала.

Зокрема:

1 (лінійність). Для будь-яких інтеґровних функцій Рис. 5 і довільних сталих

.

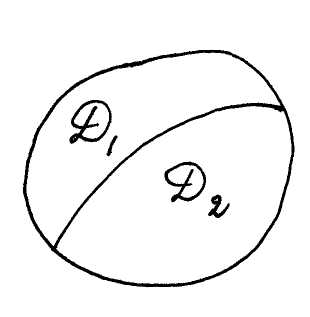
2 (аддитивність відносно області інтеґрування). Якщо область поділено на дві непересічні частини

, ,

(рис. 5), то подвійний інтеґрал по всій області дорівнює сумі інтеґралів по її частинах.