7. Наближене обчислення визначеного інтеґрала

В попередньому розділі ми розглянули деякі з надзвичайно численних застосувань визначеного інтеґрала. Успіх цих застосувань великою мірою залежать від нашої спроможності обчислювати інтеґрали, краще за все – за допомогою формули Ньютона-Лейбніца. Але формула незастосовна, якщо первісна підінтеґральної функції не виражається в елементарних функціях. В таких випадках ми можемо вдаватися до відшукання наближених значень відповідних інтеґралів.

Для достатньо простого виведення формул наближеного інтеґрування ми припускатимемо підінтеґральну функцію невід"ємною, . В такому випадку визначений інтеґрал

визначає площу криволінійної трапеції

,

обмеженої прямими , , віссю Ox і графіком функції. Отримані результати залишаються вірними і в загальному випадку.

7.1. Формули прямокутників

Поділимо відрізок на n рівних частин довжини

точками

.

Прямі Рис. 1

поділяють графік функції на n частин (рис. 1). Введімо наступні позначення для значень функції в точках поділу:

.

а) Замінюючи всі частини кривої відрізками прямих ліній

,

ми замінюємо криволінійну трапецію множиною прямокутників з сумарною площею

.

Отже,

( 1 )

б) Аналогічно, замінюючи всі частини кривої відрізками прямих ліній

,

отримуємо

( 2 )

Абсолютна похибка формул (1), (2), а саме абсолютна величина різниці інтеґрала і суми має порядок 1/n, тобто

.

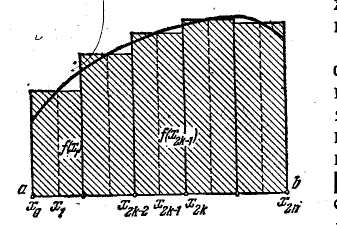
в) Поділивши відрізок на 2n рівних частин довжини

Рис. 2 точками

(рис. 2),

ми замінимо криволінійну трапецію множиною прямокутників з основами 2h, висотами і сумарною площею

Звідси

( 3 )

Абсолютна похибка формули (3) має порядок 1/n², тобто

Це означає, що формула (3) є більш точною в порівнянні з формулами (1) і (2).

7.2. Формула трапецій

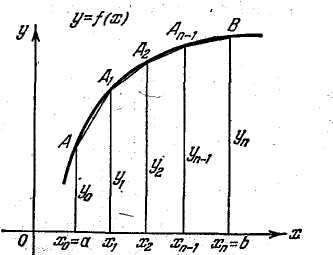Після ділення відрізка на n рівних частин

довжини

точками Рис. 3

ми ділимо на n дуг графік функції точками

(рис. 3).

Замінивши тепер всі дуги відрізками , мы замінимо криволінійну трапецію множиною трапецій з сумарною площею .

Звідси ми приходимо до наступної наближеної формули (так званої формули трапецій):

,

( 4 )

Абсолютна похибка формули (4) має порядок 1/n², тобто

.

Це значить, що формули (3) і (4) мають один і той же порядок точності.

7.3. Формула симпсона1 (формула парабол)

Розділимо (точками ) відрізок на парну кількість 2n рівних частин довжини , і нехай

- точки кривої , які відповідають точкам поділу (див. рис. 4 для випадку 2n = 6).

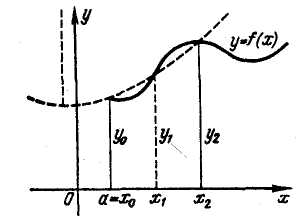Проведімо спочатку через точки па-раболу (див. рис. 4, 5). Площа фігу-ри між параболою і відріз- Рис. 4 Рис. 5 ком осі Ox дорівнює

.

■Припустімо для простоти доведення, що . Тоді ,

■

Отже, ми можемо наближено записати

.

Вчиняючи таким же чином з трійками точок

…, ,

дістаємо

.

Таким чином, ми приходимо до формули Симпсона для наближеного обчислення визначеного інтеґрала

(5)

Наприклад, у випадку n = 3, 2n = 6 (рис. 4) формула має такий вигляд:

.

Формула Симпсона (5) в порівнянні з формулами (1) – (4) , є найбільш то-чною. Дійсно, її абсолютна похибка має порядок 1/n⁴ , тобто

.

Приклад 1. Знайти наближене значення визначеного інтеґрала

.

Утворимо наступну таблицю значень арґументу і функції:

i
0	0.0	0.00	0.0000
1	0.2	0.04	0.0400
2	0.4	0.16	0.1593
3	0.6	0.36	0.3523
4	0.8	0.64	0.5972
5	1.0	1.00	0.8415
6	1.2	1.44	0.9915
7	1.4	1.96	0.9249
8	1.6	2.56	0.5487

Вона відповідає поділу відрізка на частин довжини

.

За формулою (1)

.

За формулою (2)

.

Використовуючи формулу (3), ми беремо 2n = 8, n = 4,

,

і тому

.

За формулою (4)

.

Формулою (5) ми скористаємось двічі.

Спочатку ми поділимо відрізок на 2n = 4 частин,

, , , , ,

Відповідно

, , , , , ,

і тому

Поділивши тепер відрізок на 2n = 8 частин,

,

маємо

Корисно порівняти всі отримані результаті з відомим наближеним значенням того ж інтеґрала з точністю до , а саме:

.