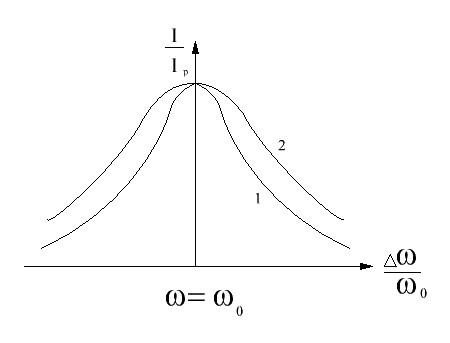
2) Зависимость тока в контуре от частоты

Амплитуда тока в контуре

разделим на - значение тока при резонансе, получим нормированное

значение тока:

Это выражение представляет собой закон изменения тока в контуре при изменении частоты. Частотная зависимость тока называется резонансной кривой. АЧХ имеет вид резонансной кривой . В области малых расстроек (в пределах полосы пропускания):

АЧХ тока в контуре при различных добротностях приведены на рисунке7(Q1>Q2)

при Q1;

при Q2;

Полосой пропускания ( ) называется такой интервал частот, на границах которого амплитуда тока падает до уровня, равного от ее

максимального значения на частоте

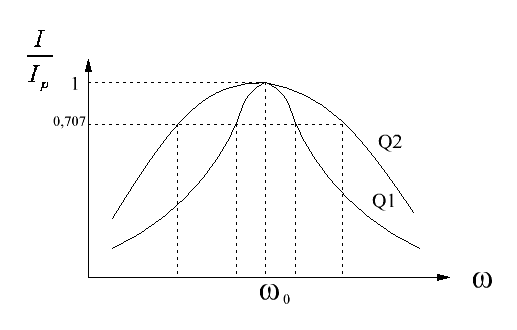
Рисунок 7

3) Передаточные функции колебательного контура

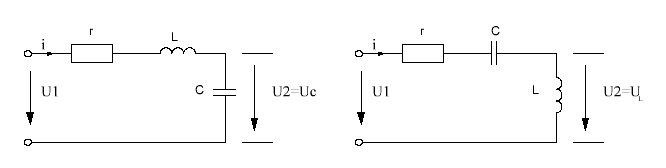
Рисунок 8а Рисунок 8б

Передаточной функцией называется величина:

При снятии выходного напряжения с емкости

При снятии выходного напряжения с индуктивности

При резонансе:

Вывод: при резонансе в последовательном колебательном контуре напряжение на каждом из реактивных сопротивлений в С2 раз превышает входное напряжение. Колебательный контур обладает свойством усиливать подведенное к контуру напряжение. Поэтому резонанс в последовательном колебательном контуре называется резонансом напряжений/

При расстройке контура:

Где -предельная резонансная характеристика.

Зависимости приведены на рисунке 9.

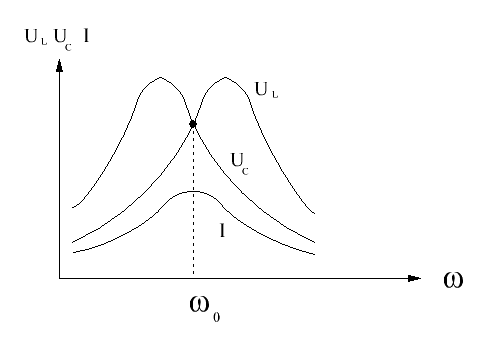
Рисунок 9

Резонансные кривые напряжения на элементах контура несколько различаются. При малых добротностях (Q<10),т.е. при больших сопротивлениях потерь наблюдаются специфические особенности кривых. Это явление объясняется тем, что максимумы смещаются относительно максимального тока, т.е. :

Значения тока на резонансной низкодобротной кривой при подходе к резонансной частоте изменяются медленно (рис 7 ), а значение при увеличении частоты от до изменяется значительно (рис 4 .). Поэтому максимальное значение произведения стремится в сторону увеличения частоты, т.е. к , вправо от резонансной частоты. В высокодобротных контурах различение между и , и незначительны.

При Q=10:

=0.9975

=1.0025

а максимумы напряжений:

При Q>10можно считать = = и

Рисунок 10

Колебательный контур питается некоторым реальным генератором с конечным внутренним сопротивлением, что может существенно повлиять на избирательные свойства колебательного контура.

Всегда, Qэ<Q т.е. при включении генератора добротность уменьшается; полоса пропускания расширяется и превышает полосу

пропускания контура .Чем больше Ri, тем меньше эквивалентная _п добротность контура Qэ и шире полоса пропускания (рис 11). Кривые зависимости или 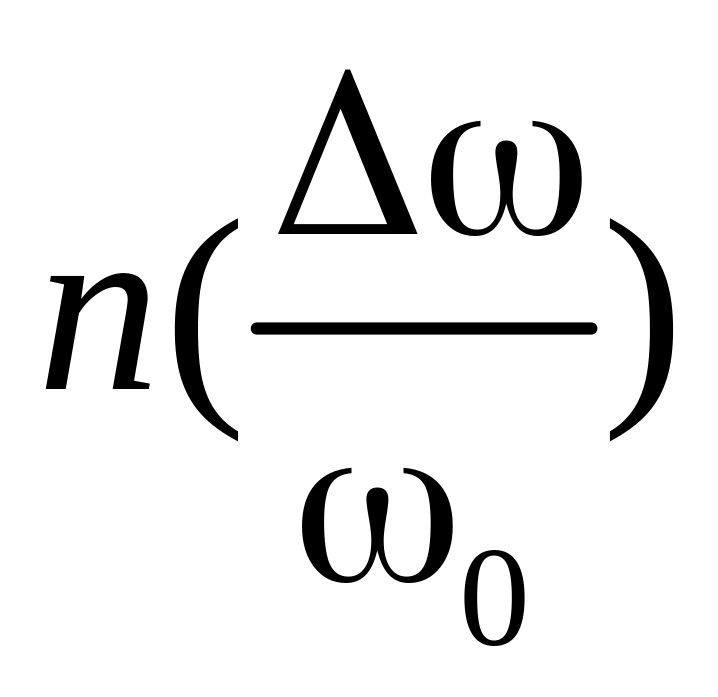при данном Q контура называются предельными резонансными характеристиками . Они могут быть реализованы только в том случае, если бы амплитуда напряжения, была бы постоянной, т.е.

Ri ген=0 (идеальный источник напряжения), чего в действительности быть I не может. Поэтому эти характеристики называются предельными.

1- АЧХ при Qк 2- АЧХ контура с Ri Qэ Qк>Qэ

Рисунок 11

- предельная АЧХ тока

Вывод: последовательный колебательный контур целесообразно

применять в том случае, когда внутреннее сопротивление источника

сигнала достаточно мало (Ri>>r).

Пример 1

Дано: L=100 мкГн; С=100 пФ;

r=10 Ом; Ri=lOO Ом (Ri>>r)

Определить: Q_3KB для R;=100 Ом (Ri>>r) и =1 Ом (Ri>>r).

Ответ: Q’_3KB =9; =90

Пример 2

Контур с теми же параметрами питается от генератора с Е=1 В, Ri=l Ом. Определить на частоте резонанса ток в цепи, U_Lp, U_Cp; угол сдвига фаз между током и напряжением на границе полосы пропускания ( ).

Ответ: =arctg ;