Цифровой фильтр и предварительная обработка спирограмм

Рассмотрим цифровой фильтр (ЦФ) с постоянными коэффици­ентами. Множество отсчетов сигнала {х(kТ)} подается на вход ЦФ в виде последовательности числовых значений х(кТ) с интервалом времени (шагом дискретизации) Т (к = 0, 1, 2, 3,..., n). При поступ­лении каждого очередного k-го входного значения х(kТ) цифровой фильтр рассчитывает очередное выходное значение сигнала y(kТ). Результаты на выходе ЦФ вычисляются с тем же шагом времени Т. Если подать на вход ЦФ простейший сигнал в виде единичного импульса

то на выходе получим сигнал {g(kT)} в виде дискретного множества числовых значений g(kT), следующих с интервалом времени Т. Этот ответный сигнал называют импульсной характеристикой цифрового фильтра.

Если подать на вход ЦФ дискретный сигнал х(кТ), на выходе фильтра сформируется отклик:

и для n-ого выходного отсчёта:

т. е. выходной сигнал определяется как дискретная свертка вход­ного сигнала и импульсной характеристики фильтра. Применив Z-преобразование к импульсной характеристике фильтра {g(kT)}, получим функцию Н(z), называемую системной функцией циф­рового фильтра:

Рассмотрим алгоритм цифровой фильтрации общего вида:

(4)

Применяя Z-преобразование к выражению (4), получаем

откуда

Частотные характеристики цифровых фильтров.

Передаточ­ная характеристика аналогового фильтра является частотно-зависимым коэффициентом пропорциональности между спектром сигнала на выходе фильтра и спектром входного сигнала :

Для анализа аналоговых фильтров в качестве входного сигнала обычно используют обобщенный гармонический сигнал , то­гда выходной сигнал имеет вид . Для определения час­тотной характеристики ЦФ на его вход подают дискретизированный обобщенный гармонический сигнал , тогда сигнал на выходе имеет вид .

Между частотной характеристикой фильтра К(ω) и его сис­темной функцией H(z) имеется простая связь:

.(5)

Следует отметить, что частотные характеристики цифровых фильтров являются периодическими функциями частоты с перио­дом повторения, равным частоте дискретизации сигнала ω_Д=2π/Т, где Т — шаг дискретизации ЦФ. По этой причине пе­ред цифровой обработкой обычно ограничивают полосу частот аналоговых сигналов специальными фильтрами нижних частот, что уменьшает негативные проявления частотных искажений дис­кретизации - наложения частот (алайзинг).

Сглаживание и численное дифференцирование. С помощью од­них алгоритмов цифровой фильтрации возможно сглаживание сигналов, с помощью других - численное дифференцирование этих сигналов [4].

Однако существуют такие алгоритмы цифровой фильтрации, которые позволяют совместить в едином алгоритме операции сглаживания и дифференцирования. Рассмотрим более подробно один из таких алгоритмов, который реализуется нерекурсивным цифровым фильтром. Входная последовательность {x(kT}} ап­проксимируется для каждого из пяти последовательных отсчетов сигнала (рис. 5) с абсциссами k = -2, -1, 0, 1, 2 полиномом p₂(t) второго порядка (параболой):

P₂(t) = A + Bt + Ct². (6)

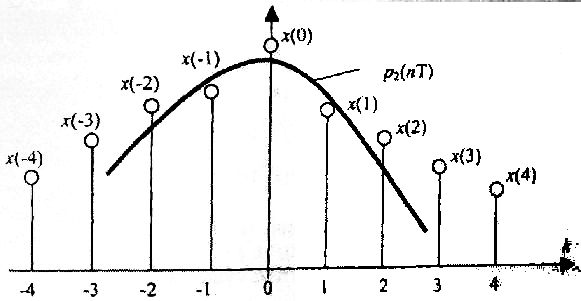
Рис. 5. Пятиточечный алгоритм цифровой фильтрации.

Неизвестные коэффициенты полинома А, В и С определяют для каждых пяти отсчетов входных данных из условия, что пара­бола (6) аппроксимирует входную последовательность методом наименьших квадратов. Качество аппроксимации оценивают сум­марной квадратичной ошибкой ε, которая является функцией коэффициентов полинома А, В и С (преобразование абсцисс вида t' = t/Т позволяет перейти к единичному шагу дискретизации, но при вычислении производных следует учесть изменение масштаба времени коэффициентом 1/7):

Условие min ε(A, В, С) можно также представить в виде сис­темы уравнений, которую называют нормальной системой уравне­ний метода наименьших квадратов:

Эта система линейных уравнений после дифференцирования выражения для ε в развернутом виде с применением упрощенно­го вида записи операции суммирования = {s(k)} выглядит следующим образом:

{1}∙А + {k}∙В + {k²}∙C = {s(k)},

{k}∙А + {k²}∙В + {k³}∙C = {k∙ s(k)},

{k²}∙А + {k³) ∙В + {k⁴}∙С = {к²∙s(k)}.

Для решения системы уравнений полезно заметить, что для k = -2, -1, 0, 1, 2:

{1} = 5, { k²}=10, { k⁴}=34 а все суммы нечетных степеней к равны нулю.

Тогда система существенно упрощается:

5∙А + 10∙C = {s(k)},

10∙В = {k∙ s(k)},

10∙А + 34∙С = {к²∙s(k)}.

Решая систему относительно коэффициентов А, В и сохраняя только центральную (k=0) точку параболы, в качестве выходного значения получаем

(7)

. (8)

Выходная последовательность при этом подобна входной по­следовательности, но содержит меньше высокочастотных помех, так как параболическая аппроксимация обеспечивает некоторое сглаживание входной последовательности.

Определяя производную со сглаживанием, с учетом масштаб­ного коэффициента преобразования координат получим

(9)

Подставляя выражение (7) в выражение (9) и применяя к ре­зультату Z-преобразование, получаем системную функцию сгла­живающего фильтра:

т. е. имеем нерекурсивный фильтр нижних частот. В соответствии с формулой (5) частотная характеристика такого фильтра имеет вид

. (9)

Частотная характеристика сглаживающего фильтра показана на рис. 6.

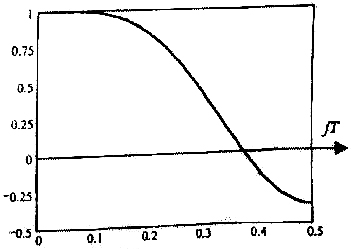
Рис. 6. Частотная характеристика сглаживающего цифрового фильтра.

Теперь найдем первую производную для функции (6):

Но для В справедливо соотношение (9). Тогда окончательно по­лучаем

(10)

Поэтому системная функция и частотная характеристика имеют вид

Этот фильтр аппроксимирует идеальную производную на низ­ких частотах не так хорошо, как другие, однако его усиление не является функцией периода дискретизации Т, как у фильтров, ап­проксимирующих по двум и трем точкам.

Рассматривая движущуюся систему координат с окном из пяти точек, мы продолжаем аналогичным образом получать новые сглаженные значения выходного сигнала цифрового фильтра и определять устойчивую к действию высокочастотных помех про­изводную входного сигнала.