1.8. Ортогональные и ортонормированные базисы подпространств
Базис подпространства называется ортогональным, если – ортогональная система векторов.
Диагональная
система векторов
образует, очевидно, ортогональный базис
пространства
.
Покажем, что каждое подпространство
пространства
обладает ортогональным базисом.
Предварительно докажем следующую
теорему.
□ Теорема 1.25. Каждую ортогональную систему ненулевых векторов из подпространства L можно дополнить до ортогонального базиса L.
Доказательство. Пусть . Из свойства ортогональных систем векторов следует, что система векторов линейно независимая и, значит, ее можно дополнить до базиса
(33)
подпространства L (теорема 1.4). Подвергнем систему векторов (33) процессу ортогонализации. После этого получим ортогональную систему ненулевых векторов
(34)
содержащую
в качестве части данную систему векторов
,…,
.
Из эквивалентности систем векторов
(33) и (34) вытекает, что каждый вектор из
подпространства
разлагается по системе векторов (34).
Линейная независимость системы векторов
(34) следует из ее ортогональности. Этим
установлено, что система векторов (34)
является ортогональным базисом
подпространства
.
■
Следствие. Каждое ненулевое подпространство обладает ортогональным базисом.
Доказательство.
Пусть вектор
и
.
Тогда
− ортогональная система, которую можно
дополнить до ортогонального базиса
подпространства
.
Базис подпространства называется ортонормированным, если является ортонормированной системой векторов. Связь между ортогональными и ортонормированными базисами устанавливается в следующей теореме.
□ Теорема 1.26. Справедливы следующие утверждения:
1. Если система векторов
−
ортогональный базис подпространства , то
−
(35)
ортонормированный базис подпространства .
2. Каждую ортонормированную систему векторов из подпрост-ранства можно дополнить до ортонормированного базиса этого подпространства.
Доказательство
1.
Так как
− базис подпространства L,
то
,
.
Теперь из ортогональности системы
следует
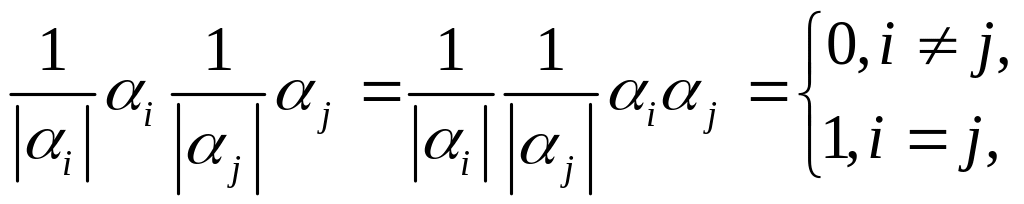
т. е. система (35) – ортонормированная система векторов и, значит, линейно независимая. Отсюда и из теоремы 1.8 вытекает, что система векторов (35) – базис подпространства L.
2. Пусть дана ортонормированная система векторов из подпространства L
,…,
.
(36)
Она является ортогональной системой ненулевых векторов. Следовательно, ее можно дополнить до ортогонального базиса подпространства L (теорема 1.25)
,…,
,
,…,
.
(37)
Умножим каждый вектор системы (37) на величину, обратную его длине. Получим ортонормированный базис подпространства L (первое утверждение теоремы 1.26)
,…,
,…,
.
(38)
Ортонормированный базис (38) содержит в качестве части данную систему векторов (36). ■
Задачи
1. Применяя процесс ортогонализации, построить ортогональный базис линейной оболочки данной системы векторов:
а) (1, 1, 1), (2, 1, 0);
б) (1, –1, 1, –1), (3, 0, –1, 1), (1, 0, 1, 1).
2. Установить, что следующие системы векторов ортогональны, и дополнить их до ортогонального базиса пространства :
а) (2, –1, 1, 0), (1, 1, –1, 1);
б) (–1, 0, 2, 1), (1, 1, 1, –1).
3. Дополнить следующие системы векторов до ортонормированных базисов пространства :
а)
,
;
б)
4.
Пусть
ортогональный базис пространства
.
Доказать, что ортогональным дополнением
линейной оболочки системы векторов
является линейная оболочка системы
.
5.
Доказать, что
– ортогональный базис пространства
,
если
и
− ортогональные базисы соответственно
подпространств
и
.
6. Доказать, что дополнением ортогональной системы до ортогонального базиса пространства является ортогональный базис подпространства
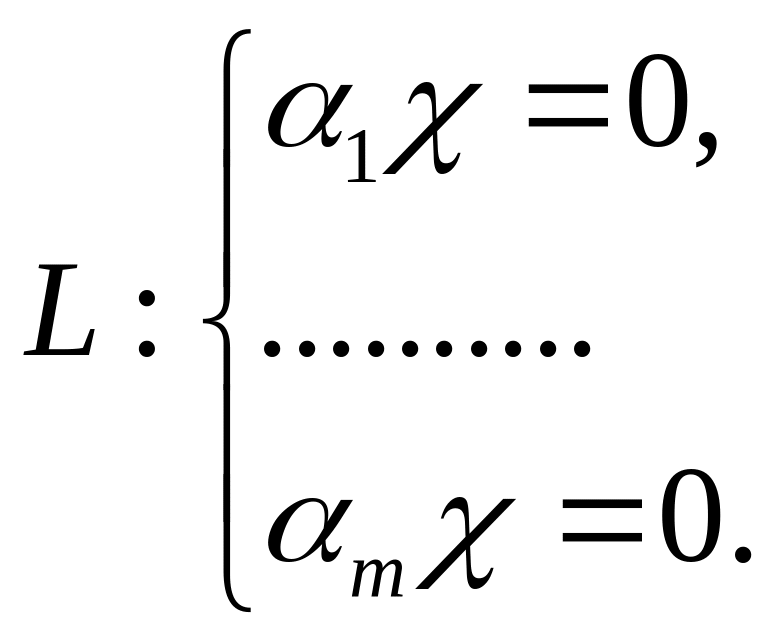
7. Найти ортогональный базис подпространства , если подпространство задано системой уравнений
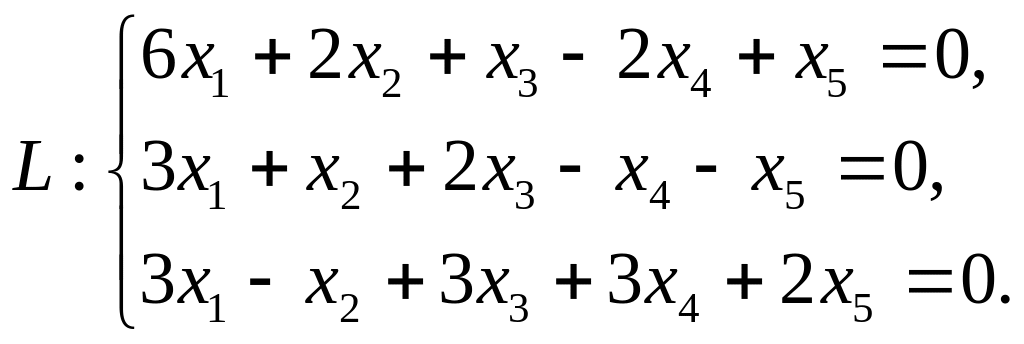
8. Найти ортонормированный базис подпространства , если подпространство задано системой уравнений
