Задача 6

В схеме, показанной на рис. 9.16, внезапно отключаются и затем вновь включаются обе линии, связывающие генераторную станцию с шинами неизменного напряжения. Параметры схемы и режима приведены на рисунке.

Определить наибольшее допустимое время перерыва в подаче энергии, при котором динамическая устойчивость системы не нарушается.

Решение. Максимальная мощность в нормальном режиме, определенная приближенно

При отключении линия

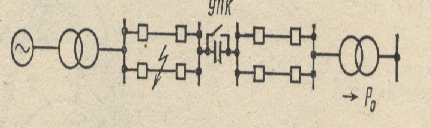
Рис.9.16.Схема исследуемой системы

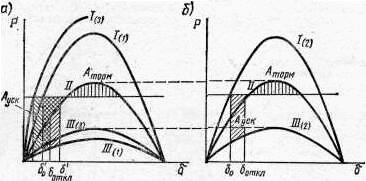
Рис. 9.17. Процессы при включении УПК:

а – случай 1 и 3; б – случай 2. Кривые /, //, /// имеют индексы, относящиеся к соответствующим случаям.

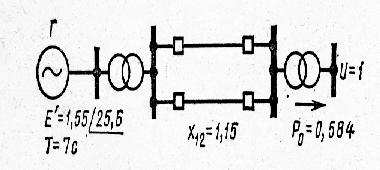
Рис. 9.18. Расчетная схема

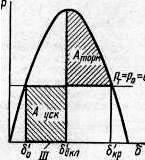
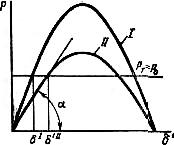
Рис.9.19. Характеристики мощности и площадки ускорения А_уск и торможения А_торм.

Применяя правило площадей, найдем согласно рис. 9.19 предельный угол включения электропередачи:

,

где δ_кр = 180 – arcsin(P₀/P_m^I) = 180 – arcsin(0,584/1,354) = 154,4⁰.

Определим предельное время включения с помощью выражения

Задача 7

В электропередаче, показанной на рис. 9.20, происходит внезапное отключение одной из двух параллельных линий. Параметры элементов электропередачи и параметры режима до отключения линии указаны на схеме.

Определить (приближенно) характер изменения угла во времени.

Решение. Расчет произведем упрощенно, заменив восходящую ветвь характеристики мощности II послеаварийного режима (рис. 9.21) отрезком прямой линии, проходящей через начало координат и точку пересечения характеристики мощности II с прямой Р_Т = Р₀. Дифференциальное уравнение движения ротора в этом случае будет иметь вид

T_J d² δ’ / d t² = P₀ – aδ’

где a = tgα.

Решение этого уравнения можно представить в виде

δ’ = P₀/a - ∆δ’ cos /T_J t

Р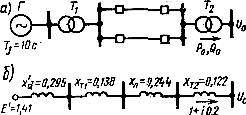 ис. 9.20. Схема (а) и ее схема замещения (б) Рис. 9.21. Характеристики

мощности

Рис. 9.22. Изменение угла δ' = f(t)

Чтобы определить Δδ' и α, входящие в последнее выражение, найдем амплитуды характеристик мощности I и II

,

тогда

а =

Изменение угла показано на рис. 9.22.

Контрольные вопросы

1. Назовите особенности статической и динамической устойчивости.

2. Что такое статические характеристики?

3. Почему появился термин «практические критерии устойчивости»?

4. Перечислите основные практические критерии устойчивости.

5. В чем состоит основное условие устойчивости простейшей электрической системы (синхронный генератор, работающий на шины неизменного напряжения)?

6. Как с помощью основного практического критерия выявляются устойчивость простейшей системы, критический режим и условия устойчивости?

7. Каковы признаки самопроизвольного изменения режима, проявляющегося в сползании, или текучести, параметров нормального режима?

8. Какие допущения, принимаемые при анализе системы, позволяют оценивать ее устойчивость по практическим критериям?

9. В чем особенности различных практических критериев и каковы наиболее целесообразные условия использования того или иного критерия на практике?

10. Укажите общее основное свойство любых устойчивых режимов, запасы статической устойчивости, определенные по разным параметрам.

11. Что такое возмущающие воздействия и большие возмущения? Приведите примеры.

12. Как записывается уравнение относительного движения для простейшего случая? Какие при этом сделаны допущения?

13. В чем заключается способ площадей? Какие допущения положены в его основу?

14. Как в общем виде формулируется правило площадей?

15. Как определяется предельный угол отключения короткого замыкания?

16. Определите запас динамической устойчивости.

17. Как проверяется устойчивость при АПВ на линиях передачи?

18. Как применяется способ площадей при проверке устойчивости системы «две станции — нагрузка»?

19. Как представить процесс изменения угла δ во времени, в чем трудности и как они разрешаются?

20. Как проводится численное интегрирование уравнения Δω = φ(δ)?

21. Как интегрируется уравнение при полном сбросе мощности?