II. Формула Пика

2.1.Решетки .Узлы.

Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные квадраты; множество всех точек пересечения этих прямых называется точечной решеткой или просто решеткой , а сами точки –узлами решетки.

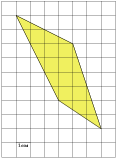
Внутренние узлы многоугольника - красные.

Узлы на гранях многоугольника - синие.

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, В - число клеток, которые целиком лежат внутри многоугольника, и Г - число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку .

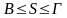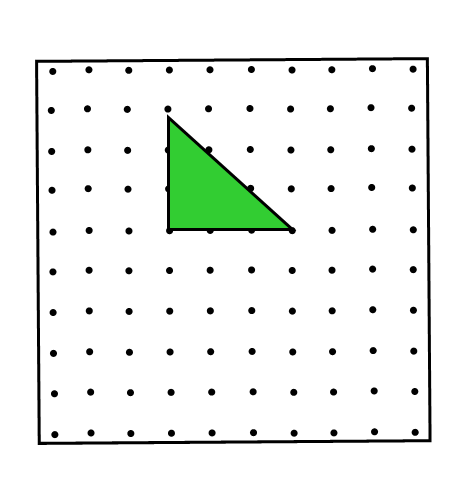
Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки.

Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника.

2.2.Триангуляция многоугольника

Любой многоугольник с вершинами в узлах сетки может быть триангулирован – разбит на «простые» треугольники.

Пусть на плоскости задан некоторый многоугольник и некоторое конечное множество К точек, лежащих внутри многоугольника и на его границе (причём все вершины многоугольника принадлежат множеству К).

Триангуляцией с вершинами К называется разбиение данного многоугольника на треугольники с вершинами в множестве К такое, что каждая точка из К служит вершиной каждому из тех треугольников триангуляции, которым эта точка принадлежит (то есть точки из К не попадают внутрь или на стороны треугольников, рис. 1.37).

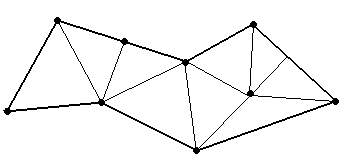
Рис. 1.37

Теорема 2. а) Любой n-угольник можно разрезать диагоналями на треугольники, причём количество треугольников будет равно n – 2 (это разбиение – триангуляция с вершинами в вершинах n-угольника).

Рассмотрим невырожденный простой целочисленный многоугольник (т.е. он связный — любые две его точки могут быть соединены непрерывной кривой, целиком в нем содержащейся, и все его вершины имеют целые координаты, его граница — связная ломаная без самопересечений, и он имеет ненулевую площадь).

Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой:

2.3. Доказательство теоремы Пика.

Пусть В — число целочисленных точек внутри многоугольника, Г — количество целочисленных точек на его границе,   — его площадь. Тогда справедлива формула Пика:

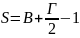
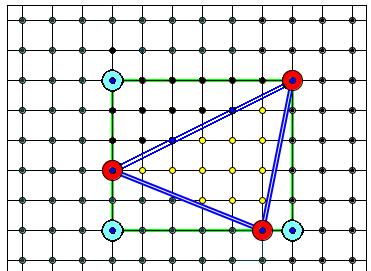
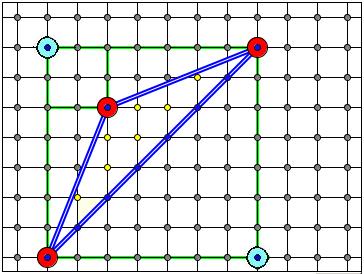
Пример. Для многоугольника на рисунке 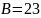  (желтые точки), Г=7, (синие точки, не забудем о вершинах!), поэтому   квадратных единиц.

1. .

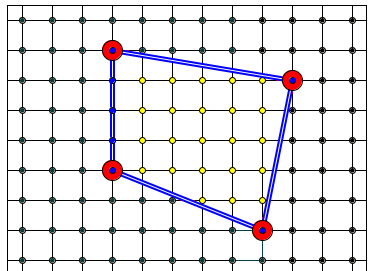
Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем В=0, Г=4 и  .

2)

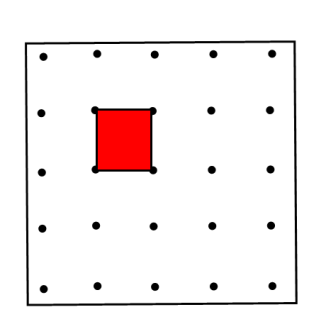
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны   и  . Имеем в этом случае ,В=(а-1)(b-1)  , Г=2a+2b, тогда по формуле Пика, 

3)

Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами   и  , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат   целочисленных точек. Тогда для этого случая 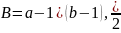Г=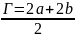 +с-1 и получаем, что  4)Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной. Пусть многоугольник   и треугольник   имеют общую сторону. Предположим, что для  формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из  добавлением  . Так как   и   имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через  и получим  — число внутренних целочисленных точек нового многоугольника, Г=Г(М)+Г(T)-2(с-2)-2 — число граничных точек нового многоугольника. Из этих равенств получаем : 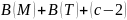 , Г=Г(М)+Г(T)-2(с-2)-2 . 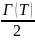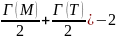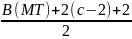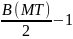Так как мы предположили, что теорема верна для   и для   по отдельности, то S(MT)+S(M)+S(T)=(В(М)+ -1)+В(T)+ -1)=( В(М)+ В(T))+( =Г(MT)-(c-2)+ -2= Г(MT)+ .Тем самым, формула Пика доказана.