3.1 Приклад розв’язання завданНя 1

1. Аналіз виразу (1.1) показує, що поле, яке потребує дослідженню утворюється магнітними хвилями, так як .

. (3.1)

Комплексна амплітуда вектора напруженості електричного поля:

. (3.2)

Комплексна амплітуда вектора напруженості магнітного поля:

.(3.3)

Розрахуємо необхідні величини і коефіцієнти.

; (3.4)

; (3.5)

[м]; (3.6)

[м]; (3.7)

[рад/с]; (3.8)

[Ом]; (3.9)

[м²]; (3.10)

[А/м] ([В/м]); (3.11)

[рад/с]. (3.12)

Підставивши числові значення величин у формули (3.2) і (3.3), запишемо вирази для комплексних амплітуд векторів напруженості електричного і магнітного полів.

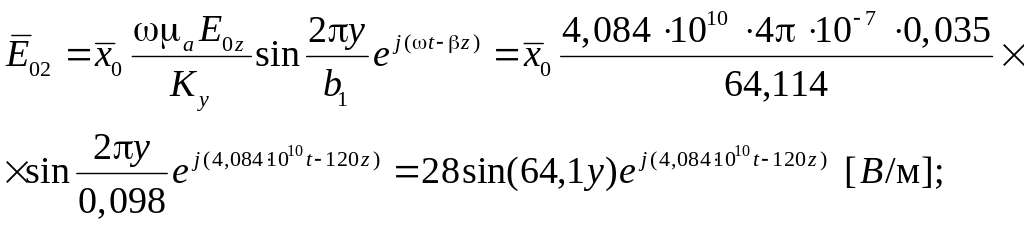(3.13)

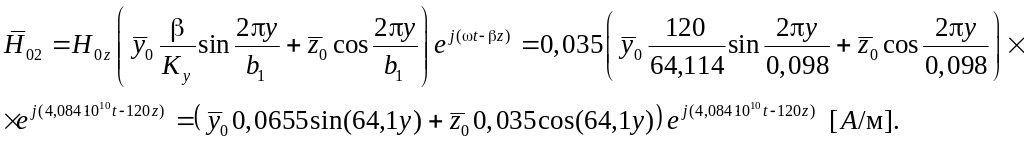(3.14)

2. Знайдемо напруженості електричного та магнітного полів у хвилеводі 1 в точці з координатами (x,y,z) у даний момент часу:

.

[В/м]; (3.15)

[А/м]; (3.16)

[А/м]. (3.17)

3. Визначимо напрямок подачі енергії у хвилеводі в даний момент часу в даній точці простору (див. рис.3.1)

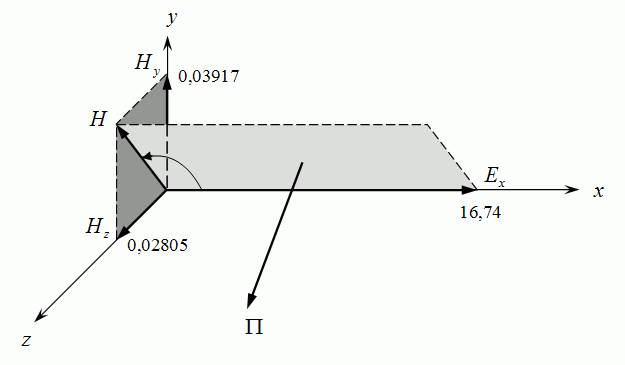
Рис.3.1 Напрямок подачі енергії у хвилеводі

3.2 Приклад розв’язання завданНя 2

1. Визначимо хвилі, які можуть поширюватись у хвилеводах 1 і 3. Номера хвиль вищого порядку вибираємо довільно. Розрахунки проведемо за формулами (3.18) – (3.22). Результати зведемо у таблицю 3.2.

; (3.18)

; (3.19)

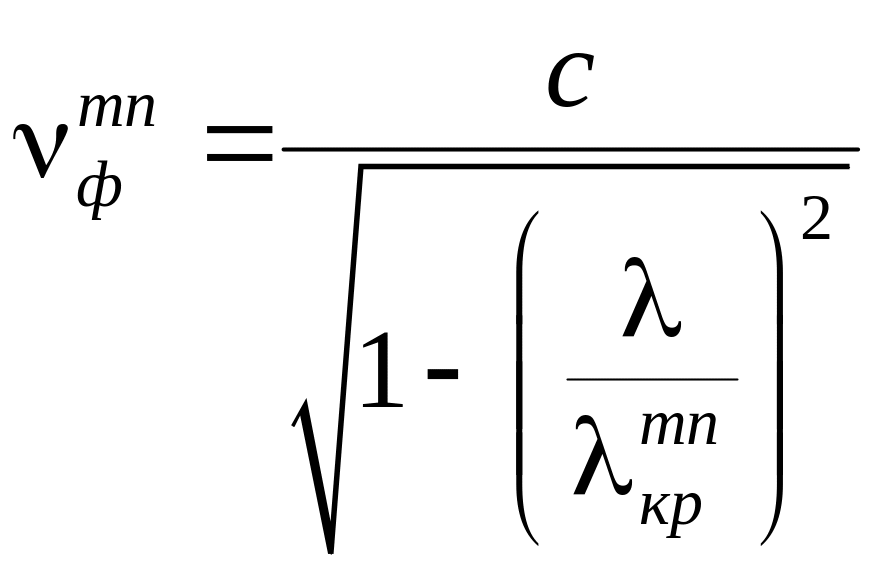; (3.20)

; (3.21) . (3.22)

Таблиця 3.2 – Параметри хвиль у хвилеводі 1

		[м]	[ГГц]	[м/с]	[м/с]	[Ом]
0	1	0.196	1.531	3.087	2.916	388
0	2	0.098	3.061	3.401	2.646	427
0	3	0.065	4.592	4.239	2.123	533
1	0	0.392	0.765	3.021	2.979	380
1	1	0.175	1.711	3.110	2.894	391
1	2	0.095	3.155	3.431	2.623	431
1	3	0.064	4.655	4.299	2.094	540
2	0	0.196	1.531	3.087	2.916	388
2	1	0.139	2.165	3.182	2.829	340
2	2	0.088	3.423	3.529	2.550	443
2	3	0.062	4.840	4.495	2.002	565
3	0	0.131	2.296	3.207	2.807	403
3	1	0.109	2.759	3.313	2.716	416
3	2	0.078	3.827	3.711	2.425	466
3	3	0.058	5.134	4.891	1.840	615

У хвилеводі 3 поширюються хвилі

[м];

[м];

[м].

Згідно завдання у хвилеводі 3 поширюється основна хвиля, тобто та, що має найбільшу довжину, а саме . Знайдемо її основні параметри

[ГГц]; (3.23)

[м/с]; (3.24)

[м/с]; (3.25)

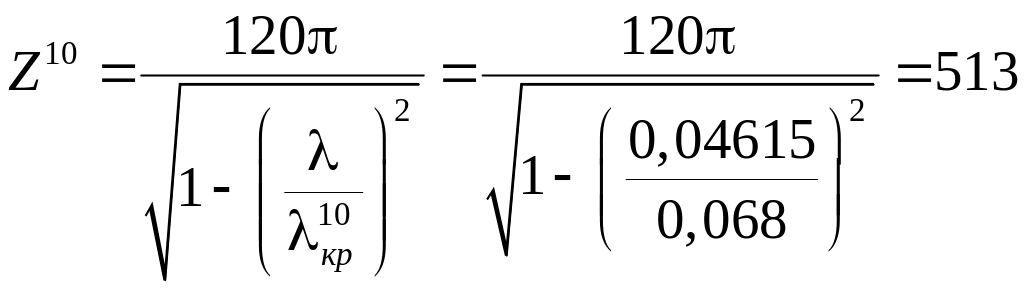[Ом]. (3.26)

Зобразимо структуру поля хвилі в різних перерізах хвилеводу 1 (див. рис.3.2). Структура хвиль у хвилеводі 3 така сама, тількі зміняться розміри поперечного перерізу.

2. Діапазон частот поширення хвиль в хвилеводі 1 для:

: [ГГц], [ГГц];

: [ГГц], [ГГц];

: [ГГц], [ГГц].

3. Діапазон одномодового поширення хвилі в хвилеводі 1:

[ГГц]. (2.10)

Діапазон одномодового поширення хвилі в хвилеводі 3 від 0 до 4,412 ГГц:

[ГГц]. (2.11)

Рис.3.2 – Структура поля у хвилеводі 1

4. Побудуємо графіки залежності фазової та групової швидкості від частоти (див. рис.3.3). Результати розрахунків зведемо в таблицю 3.3.

Таблиця 3.3 Дані для побудови графіків

№	1	2	3	4	5	6	7	8
[ГГц]	3,061	4	5	6	7	8	9	10
[м/с]		4,661	3,794	3,488	3,336	3,247	3,19	3,151
[м/с]	0	1,931	2,372	2,58	2,698	2,772	2,821	2,856

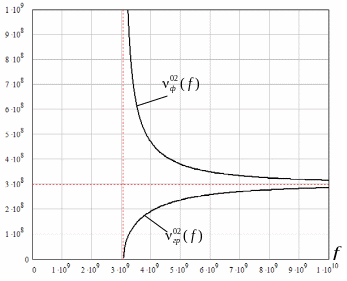
Рис.3.3 – Графіки і