28. Обнаружение сигнала на фоне помех.

Системы связи, радиолокации, управления решают задачи, связанные с передачей и приемом сигналов, подверженных искажающему действию различного рода помех. Результатом воздействия помех является частичная или полная потеря полезной информации, содержащейся в передаваемых сигналах. В связи с этим возникает ряд проблем, в том числе проблема рационального конструирования (синтеза) системы, состоящая в отыскании оптимальной по некоторому критерию качества процедуры обработки наблюдаемого процесса.

В общем случае задача обнаружения сигнала при наличии помех, состоит в том, чтобы по результатам обработки наблюдаемого процесса, который может быть либо только помехой, либо комбинацией полезного сигнала, содержащего в закодированном виде полезную информацию, и помехи, решить, содержится ли полезный сигнал в принятом или нет.

Как сигнал, так и помехи являются, вообще говоря, случайными процессами, причем наши суждения об этих процессах базируются на результатах наблюдений, представляющих либо конечное множество чисел (дискретная выборка), либо одну или несколько непрерывных реализаций процесса (на конечном интервале времени). Это обстоятельство определяет статистический подход к обработке наблюдаемых процессов с целью извлечения полезной информации. Точка зрения на прием сигналов как статистическую задачу cтaлa традиционной в современной радиотехнике.

Формально обнаружение и различение представляет проверку статистических гипотез о характеристиках случайной величины или случайного процесса, а выделение—оценку параметров или фильтрацию.

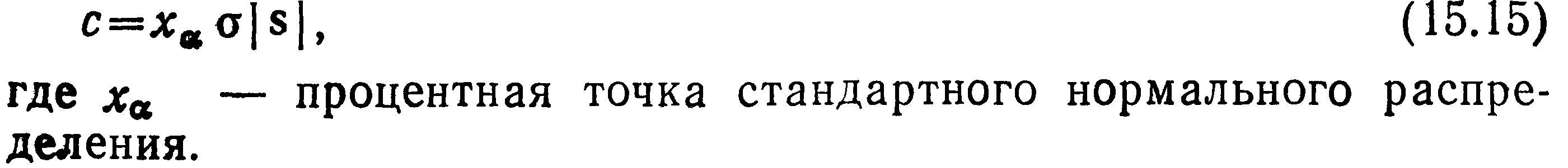
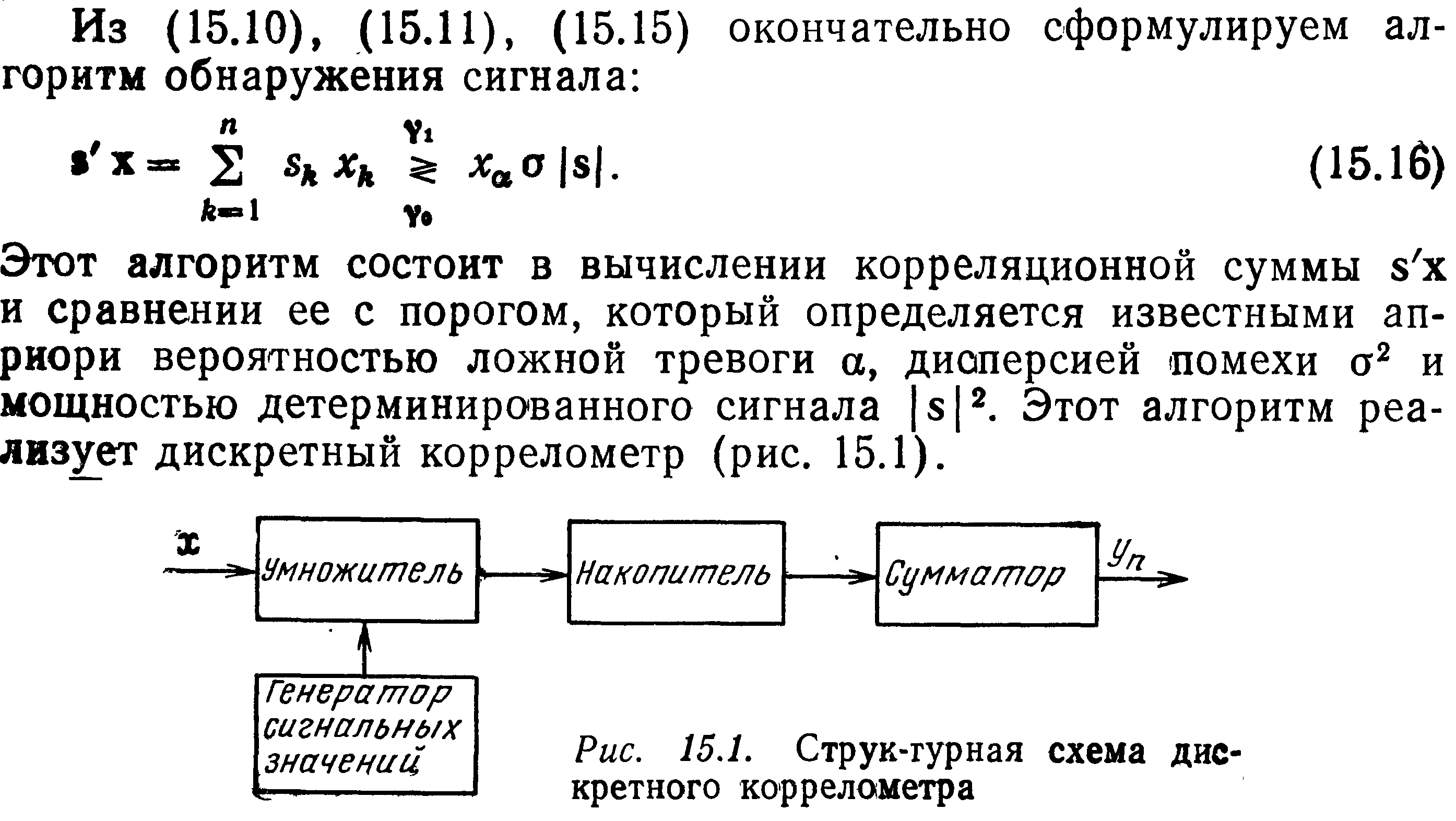
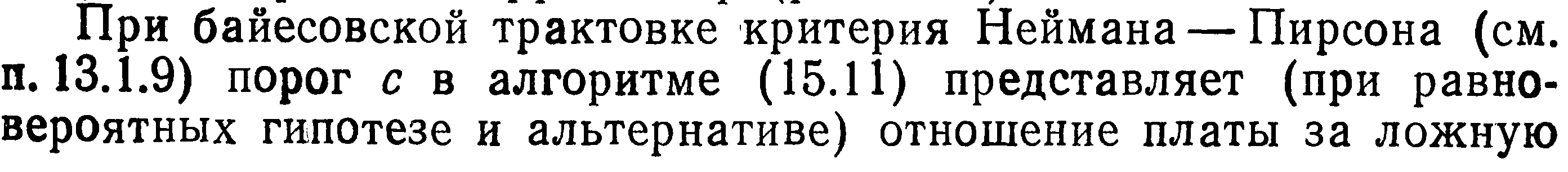
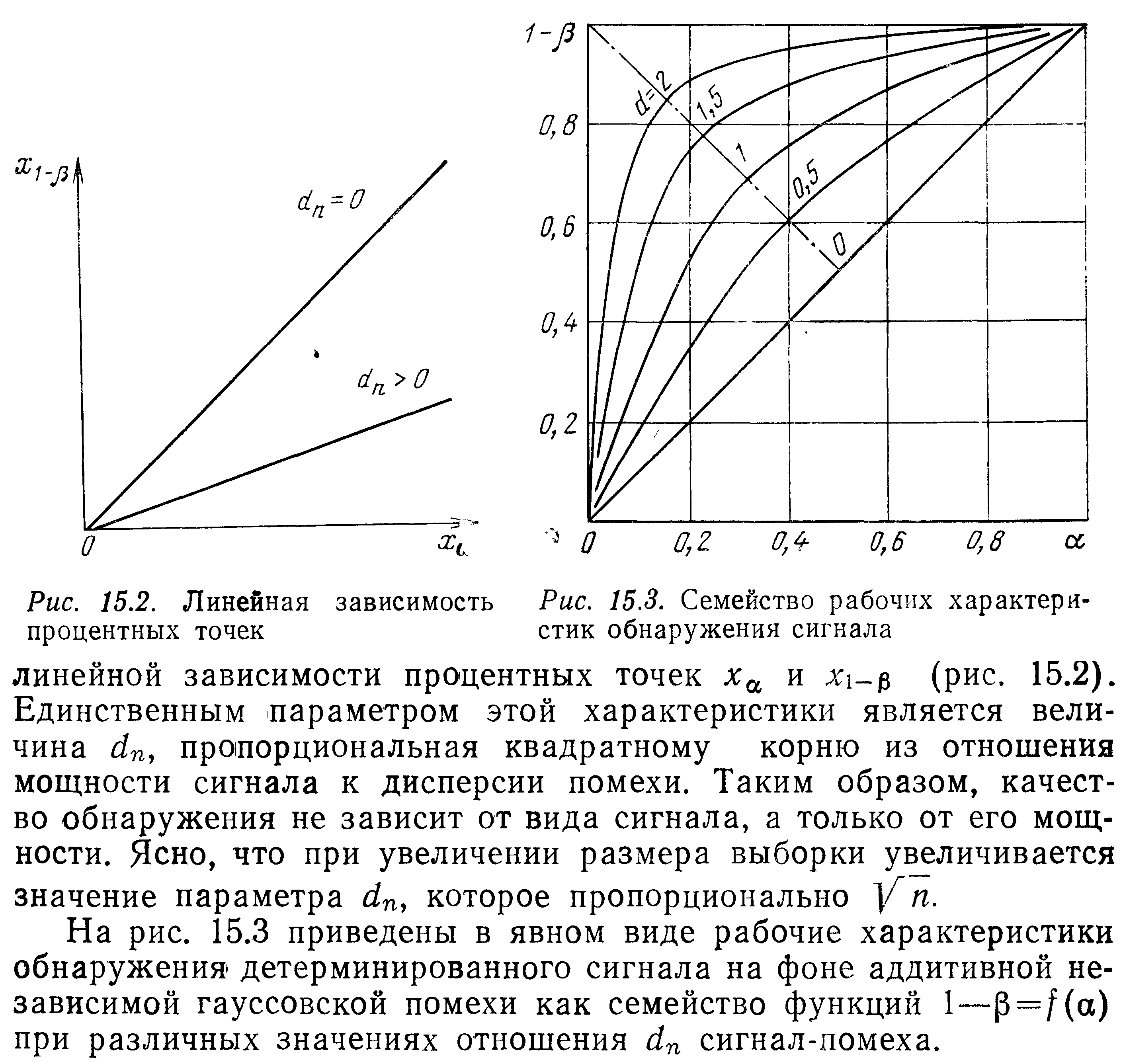
*Теория статистической радиотехники. Левин. 3е Изд. 1989г. стр.417-422.

29. Обнаружение стохастического сигнала.

Практическая часть.

Когда нет сигнала (гипотеза Н) наблюдаем шум с нулевым средним и некой дисперсией, а также нулевой корреляцией. Когда появляется сигнал (альтернатива К) также появляется коэф. корреляции r и появляется дисперсия сигнала.

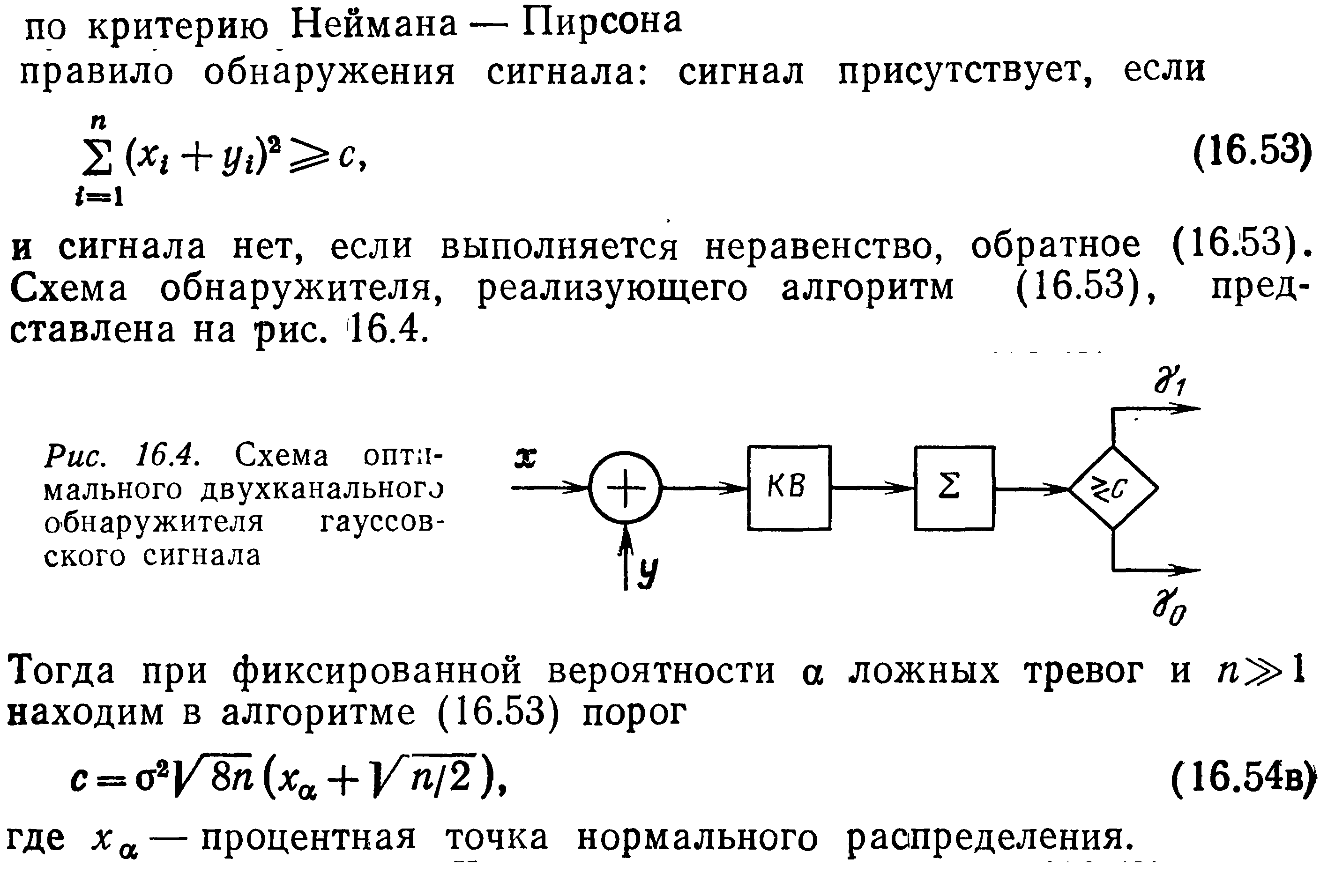
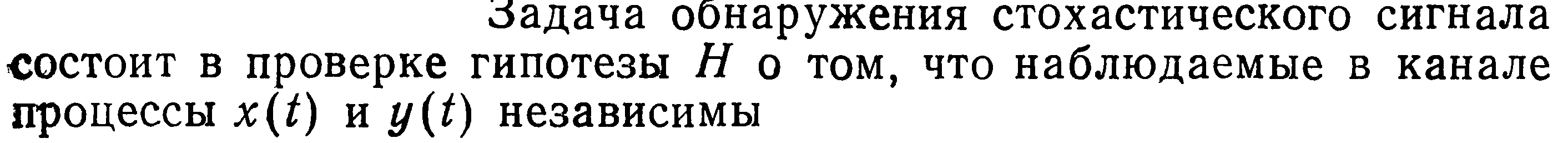
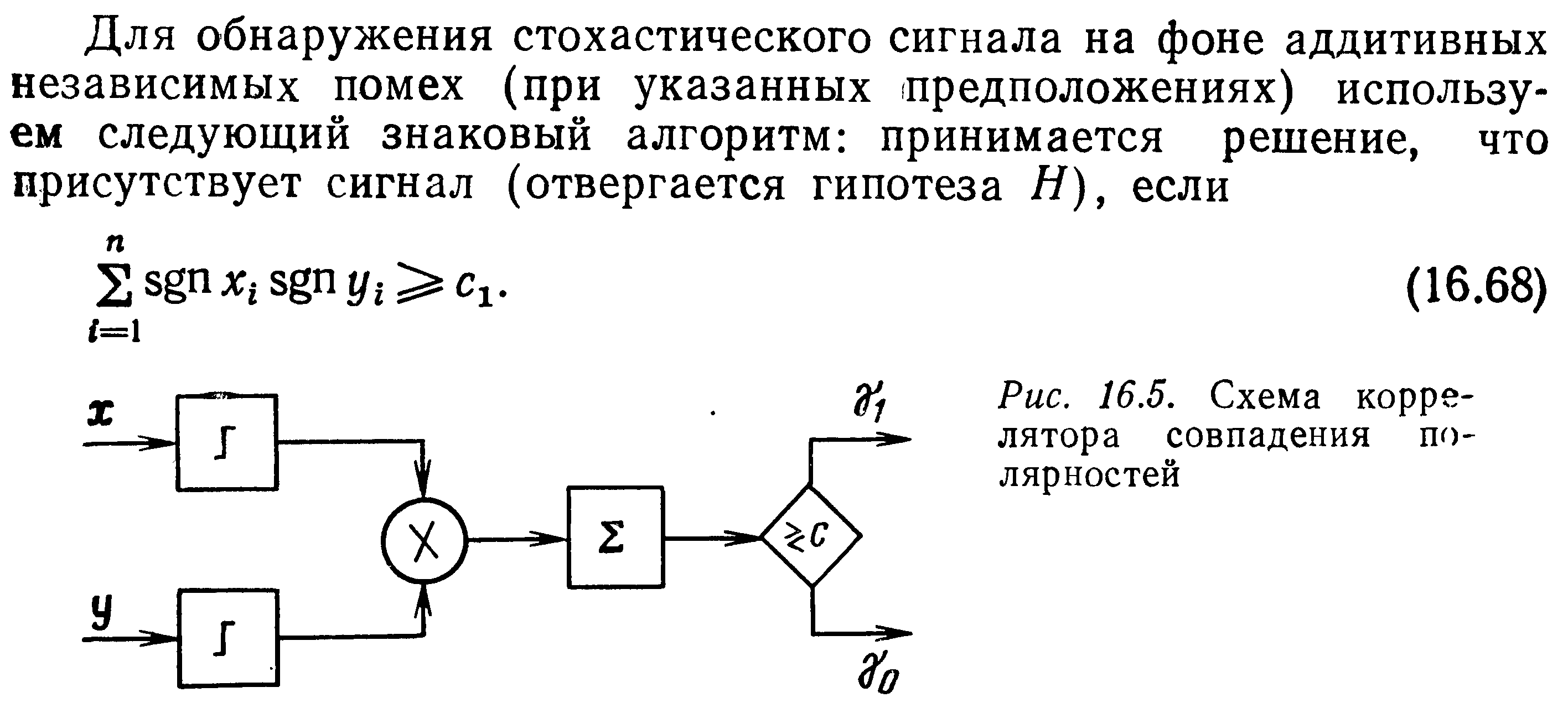
sgn(х): функция равна 1, если x>0, и равна -1, если x<0.

Смысл состоит в том что мы принимаем выборку сигнала, отсчетам из выборки ставим в соответствие знак + или - , при помощи sgn(x). Далее умножаем сигналы из двух каналов друг на друга и суммируем полученные значения на интервале одной выборки с количеством отсчетов n в каждой выборке. Если полученное значение превысит порог, то считаем сигнал есть. Если порог не превышен, то считается сигнала нет.

30. Различение сигналов.

Оптимальный алгоритм. Постановка задачи.

Рассмотрим наиболее общую структурную схему системы передачи информации (рис. 20.1). Предположим, что источник информации передает m+1 сообщений, которым соответствуют сигналы s₀(t), ..., s_m(t). На входе приемника наблюдается смесь одного из переданных сигналов со случайной помехой, искажающей сигнал при его прохождении через канал связи. Задача различения сигналов на фоне помех состоит в том, чтобы используя заранее выработанное правило, вынести решение о том, какой из m+1 возможных сигналов содержит наблюдаемый процесс.

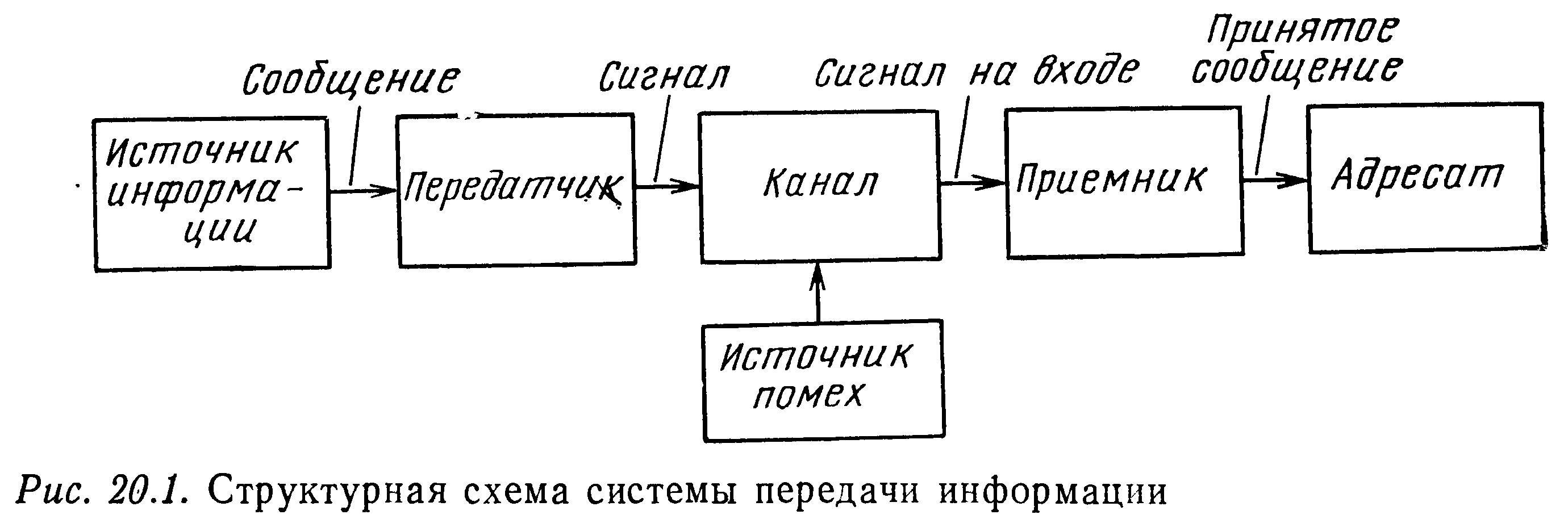
Обозначим через x(t) реализацию случайного процесса X(t), наблюдаемую на интервале 0≤t≤T на входе приемника. Предположения о том, что был передан тот или иной сигнал, формализуются в виде статистических гипотез H0, ..., Hm, где Hi — гипотеза о том, что был передан сигнал Si(t). Если верна гипотеза Hi, то случайный процесс

где ξ(t) —случайная помеха, а символ характеризует взаимодействие сигнала Si(t) с помехой ξ(t) чаще принимается что это аддитивная помеха — стационарный центрированный гауссовский случайный процесс с известной корреляционной функцией.

Помеха ξ (t) предполагается аддитивной и, следовательно, символ означает суммирование.

Общая формулировка задачи различения сигналов, приведенная выше, должна быть дополнена априорными данными. Сведения о том, как часто передаются те или иные сигналы, можно использовать для задания априорного распределения вероятностей гипотез. (Нужно до опыта иметь априорные данные о том, что мы вообще принимаем. Если мы ничего не знаем о принимаемом сигнале – значит не надо принимать такой сигнал вообще. *Климов)

- априорная вероятность.

Различение сигналов (продолж. из др. учебн.).

Наряду с задачей обнаружения сигнала по некоторой реализации процесса на входе приемного устройства, который мог быть только шумом или суммой сигнала и шума, во многих приложениях возникают более сложные задачи. Так, например, наблюдаемый процесс х (t) может быть суммой шума и сигнала, одного из заданной совокупности сигналов s₀(t), ..., s_m(t). Необходимо по принятой реализации на интервале (-Т;Т) процесса х(t) принять решение, какой из указанных сигналов в действительности присутствует в наблюдаемом процессе.

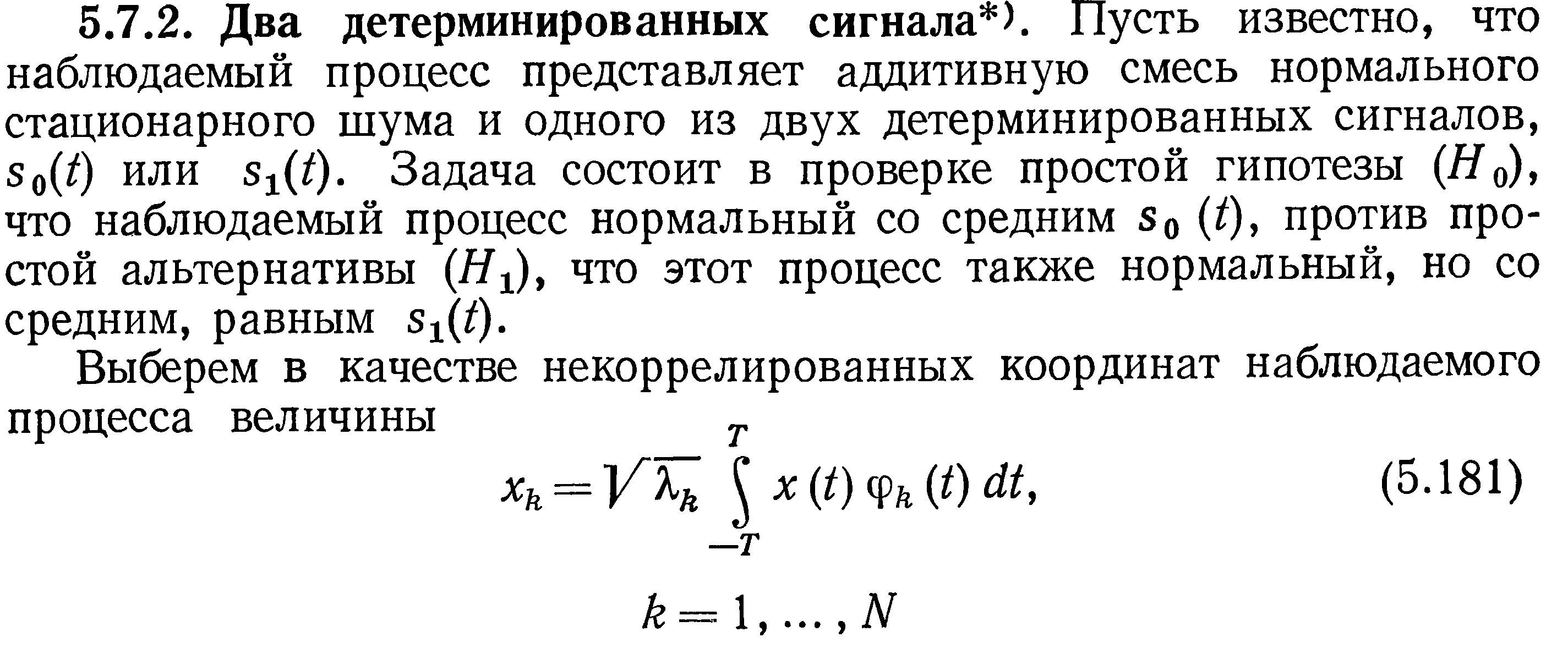
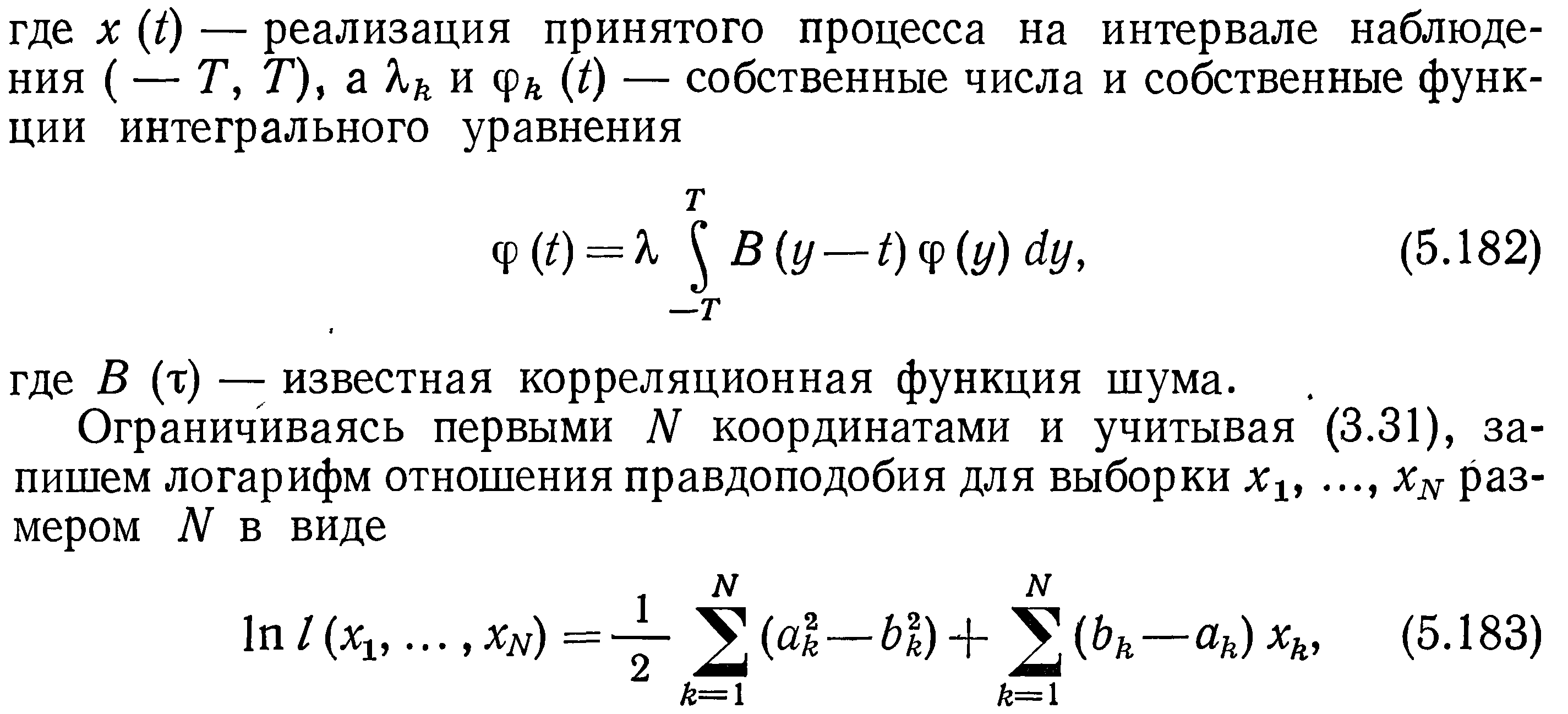
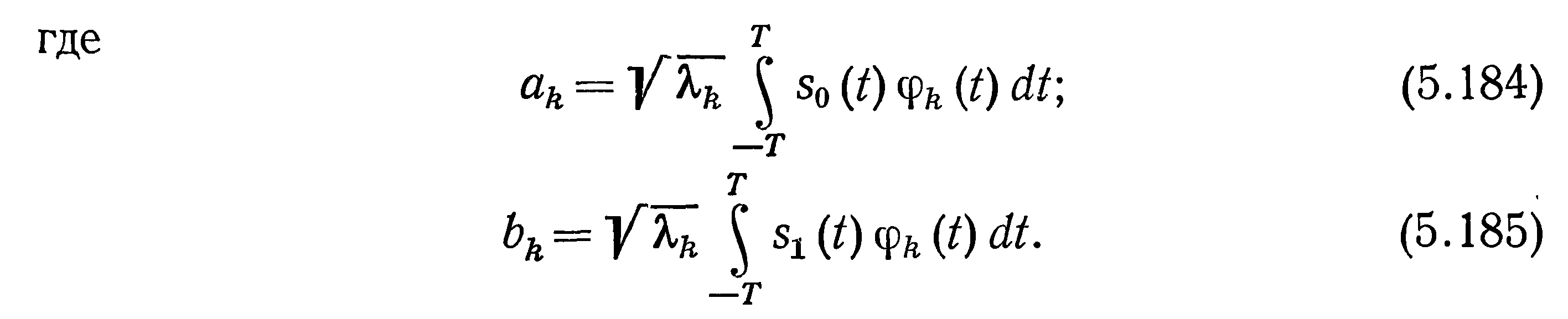
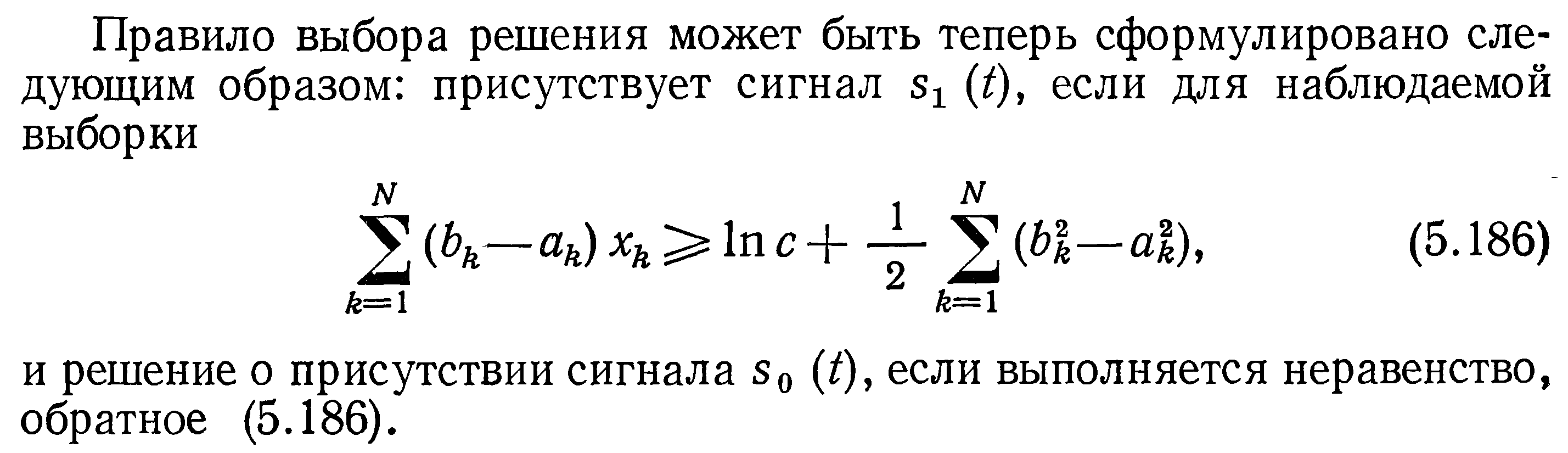
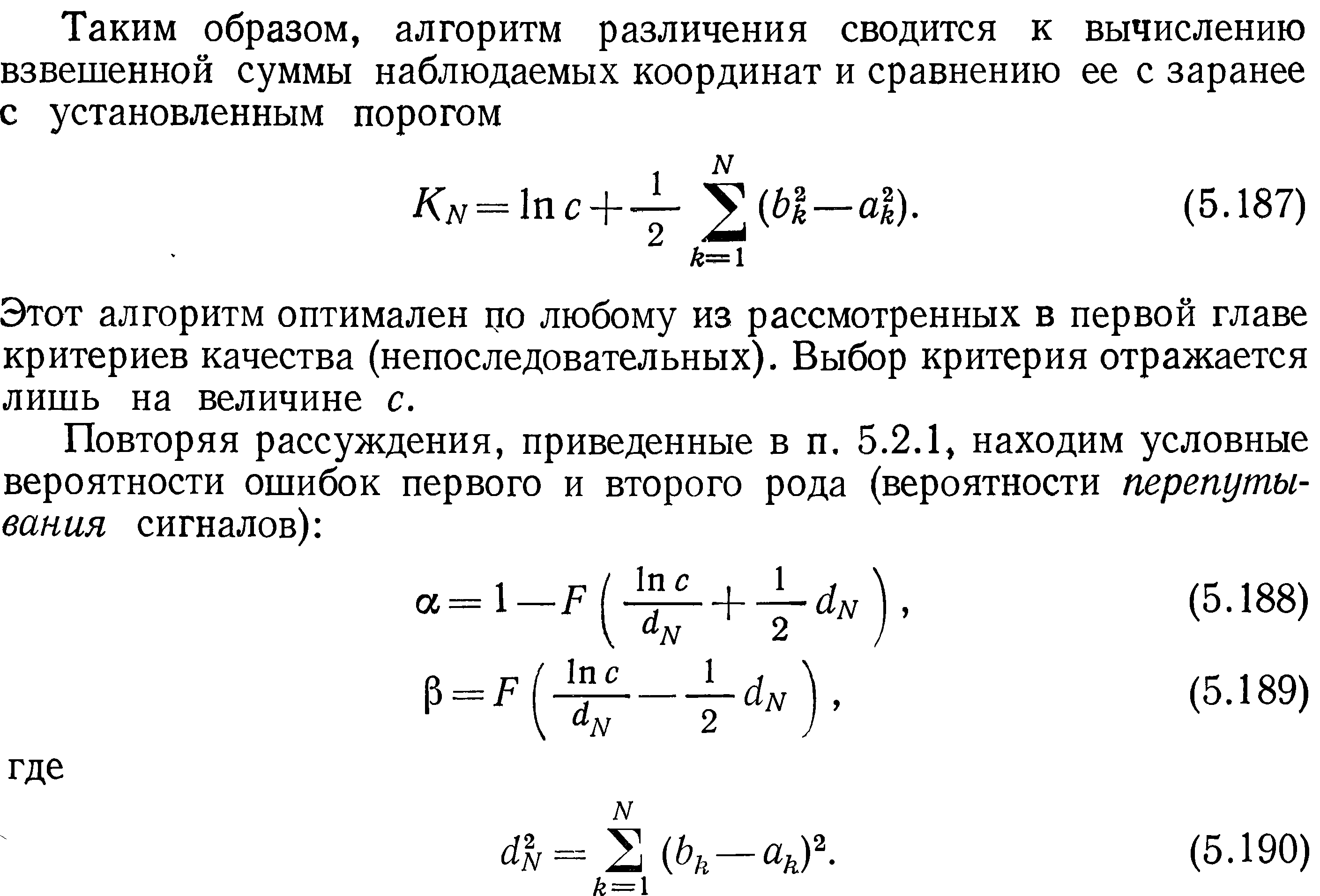
*Теория статистической радиотехники. Левин. Том 2. 1975г. стр.294-296.