13. Вычисление поправок в коррелатном способе и заключительный контроль уравнивания.
Вычисление поправок
[qa1a1]k1 + [qa1a2]k2 + … + [qa1ar]kr + w1 = 0
[qa1a2]k1 + [qa2a2]k2 + … + [qa2ar]kr + w2 = 0 (1)
…………………………………………………….
[qa1ar]k1 + [qa2ar]k2 + … + [qarar]kr + wr = 0
Равенства (1) представляют собой систему нормальных уравнений коррелат, в которой число уравнений равно числу неизвестных.
Получив из решения уравнений коррелаты, находят поправки υi в результаты измерений. Их удобнее всего вычислять по формуле:
(2)
Т.о. для вычисления поправки Vi, коррелаты умножаем на коэффициенты условных уравнений a1i, a2i, a3i, полученные произведения складываем и сумму умножаем на обратный вес qi.
Равенства (2) называют коррелатными уравнениями поправок. Из этих равенств могут быть найдены искомые поправки υi, если будут известны коррелаты kj.
После вычисления поправок υi, выполняются контроли: [Pυ2] = - [kw], подтверждающие правильность вычисления поправок υi.
Заключительный контроль уравнивания
Вычисленные поправки необходимо подставить в систему условных уравнений:
a11v1 + a12v2 + a13v3 +... + a1nvn + w1 = 0
a21v1 + a22v2 + a23v3 +... + a2nvn + w2 = 0
a31v1 + a32v2 + a33v3 +... + a3nvn + w3 = 0
…………………………………………… (3)
ar1v1 + ar2v2 + ar3v3 +... + arnvn + wr = 0
aij – коэффициент при поправках к измерениям
i - номер уравнения
j – номер измерения
Остальные невязки должны равняться нулю в пределах точности вычислений. Если заключительный контроль выполняется, то вычисляются уравненные значения измеренных величин по формуле: X’i = Xi + υi.
X’i – уравненные результаты измерений;
Xi – результаты измерений;
υi – поправки в результаты измерений.
Невязки всех условных уравнений вычисленных по уравненным результатам измерений, должны быть равны нулю.
14. Оценка точности в коррелатном способе.
Под оценкой точности подразумевается определение СКО измерений и СКО функций измеренных величин после уравнивания.
1) определяем СКО
единицы веса:
,
где Р – веса измеренных величин, принятые до уравнивания,
υ – поправки, полученные из уравнивания,
r – число избыточных измерений;
2) ошибка самой
ошибки единицы веса:
;
3) ско на 1 км хода:
,
где С - постоянная, принятая при вычислении
весов измерений.
.
3) СКО весовой
функции
.
Весовая функция - функция уравненного значения измеренной величин, составляемая для оценки точности.
15. Выбор параметров и составление уравнений в параметрическом способе.
В качестве параметров чаще всего выбираются искомые величины: при нивелировании - отметки пунктов, в плановых сетях - координаты. Число параметров должно быть таким, чтобы через параметры и исходные данные можно было выразить все результаты измерений.
Выбирают необходимые неизвестные (параметры), точные значения которых Хj (j=1,2..k), через которые выражают истинные значения результатов измерений Уi (i=1,2..n) в виде функций:
Уi = ƒi (Х1,…,Хn), (1) причем n >= k.
Эту систему уравнений (1) называют исходной системой связи. Выбор необходимых неизвестных – важный момент в параметрическом способе уравнивания, т.к. от него зависит степень сложности решаемых уравнений → объем вычислительных работ.
Т.к. истинные
значения Уi
не известны, то нельзя определить и
точные значения Хj.
Однако в
силу переопределенности исходной
системы вместо Уi
и Хj
можно подобрать уравненные значения
и
такие, что
=
f(
),
(2)
причем
=
+
,
где - измеренное значение функции,
-поправка.
Систему уравнений (2) необходимо привести к линейному виду. Разложив для этого функции fi( ) в ряд Тейлора и ограничиваясь линейными членами разложения, получим:
+
или
=
,
(3)
где свободный член
(4),
здесь
-
приближенные, однако близкие к точным
значениям параметров. Первое слагаемое
в формуле (4) представляет приближенное
значение функции. Коэффициенты
в
ф-ле (3) суть частные производные
,
,
,
взятые по уравненным значениям параметров, но вычисленные при их приближенных значениях.
Уравнение (3) называют системой параметрических уравнений поправок.
В параметрическом способе решение приводит к непосредственному получению уравненных неизвестных (параметров).
Рассмотрим на примере нивелирной сети.
1 ход: М20 – Rp1 – Rp2 – M21
2 ход: М21 – Rp2 – Rp3 – M22
3 ход: М22 – Rp3 – Rp1 – M20
1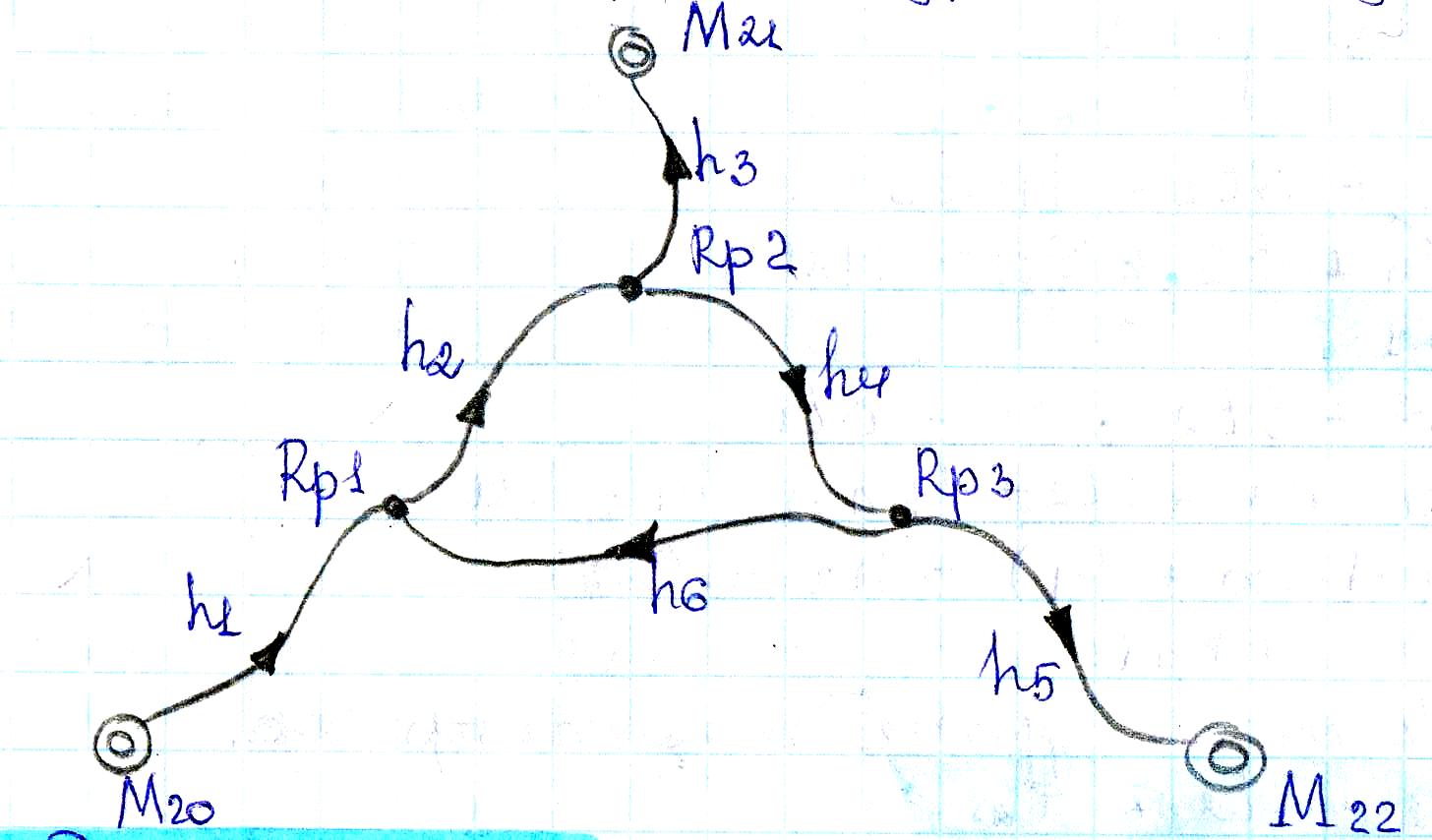
)Выбор
параметров: число параметров д.б. таким,
чтобы через них можно было выразить
все результаты измерений
t10= H1 = Hm20 + h1
t20= H2 = Hm21 – h3
t30= H3 = Hm22 – h5
2) Вычисление приближенного значений параметров. Вычисление проводится по кратчайшему пути:
ť1 = Hm20 + h’1, ť2.. ť3..
3)Составление уравнений связи: число уравнений связи равно числу рез-тов измерений:
h'i= hi+Vi;
h’i – уравненные результаты измерений;
hi – результаты измерений;
υi – поправки в результаты измерений.
t'i = ťi+δti,
t – уравненное значение параметров;
t0 – приближённое значение параметров;
δti, – поправка в приближённое значение параметров.
получаем систему равенств: h1’= t1 – HM20;
Так же h1’ = h1 + V1
а так как t1 = t10+ τ1 => получаем равенство:
h1 + V1= t10 + τ1 - Hm20 => подставляем в последнее выражение t10 = Hm20 + h1 и получим
V1 = τ1
Аналогично получаем и другие поправки:
V2 = - τ1 + τ2 + l2
V3 = - τ2
V4 = - τ2 + τ3 + l4
Если кроме τi остаются величины, то их обозначают за l - свободный член уравнения поправок.
При уравнивании плановых сетей неизвестные поправки измеренных величин представляются в виде линейных функций, в которых аргументами являются:
1) поправки ξ и η к приближенным координатам определяемых пунктов;
2) поправки ориентирования δz на станциях;
3) свободные члены l.
Т.е. поправка υ в каждое измеренное направление представляется в виде параметрического уравнения связи:
υik = φ (δzi, ξi, ηi, ξk, ηk, lik)
или
υi1 = - δzi – аi1*ξi - bi1*ηi + аi1*ξ1 + bi1*η1 + li1
υi2 = - δzi – аi2*ξi - bi2*ηi + аi2*ξ1 + bi2*η1 + li2
…………………………………………………(1) – редуцированные нормальные уравнения.
Число уравнений поправок = числу измеренных направлений в сети; оно всегда больше искомых поправок приближенных координат и поправок ориентирования на станциях. Подчинив поправки направлений условию [pυ2] = min, получим однозначные значения поправок координат и поправок ориентирования на станции.