
- •1). Машины и их классификация.
- •3) Метод векторных уравнений и их графическое решение в форме планов положений, скоростей и ускорений.
- •4) Балансировка роторов.
- •5) Статическое уравновешивание рычажных механизмов
- •8). Постановка и содержание задачи проектирования схем механизмов
- •9) Динамика машин и механизмов.
- •10), 40) Метрический синтез типовых рычажных механизмов.
- •10). Понятие о коэффициенте неравномерности средней скорости и о угле давления в рычажном механизме.
- •11) Механическая работа, энергия и мощность.
- •12). Эвольвентное зацепление и его свойства
- •15). Определение инерционной нагрузки звеньев механизма.
- •16) Многокритериальность задач проектирования.
- •17) Условие статической определимости кинематической цепи
- •21) Уравновешивающая сила (момент) и ее расчет методом н.Е. Жуковского
- •22). Постановка задачи синтеза планетарных механизмов.
- •23). Понятие о динамической модели машины.
- •25). Определение параметров динамической модели машины
- •26) Критерии работоспособности и угол давления при передаче движения в высшей кинематической паре.
- •27). Уравнения движения динамической модели
- •29). Уравнение движения динамической модели в дифференциальной форме.
- •30). Зубчатые передачи
- •31). Механические характеристики машин.
- •32). Качественные показатели эвольвентной передачи.
- •33). Неравномерность движения и методы ее регулирования.
- •34). Методы изготовления эвольвентных зубчатых колес.
- •35). Вибрации и колебания в машинах и механизмах.
- •37). Механический кпд
- •38). Коэффициент удельного скольжения.
- •41). Циклограмма работы кулачкового механизма
- •42). Цель и задачи метрического синтеза механизмов.
- •45).Коэффициент удельного давления.
- •47). Этапы синтеза
- •47) Алгоритм проектирования кулачкового механизма по допустимому углу давления
25). Определение параметров динамической модели машины
Рассмотрим
механическую систему и ее динамическую
модель. Равенство работ
можно рассматривать как равенство
мощностей
![]() .
.
Суммарная мощность внешних сил:
для механической системы:
![]() для
модели:
для
модели:
![]() или
или
![]() ,
,
где Vпр – скорость точки приложения приведенной силы.
Из
уравнения для правых частей получаем
формулы для определения приведенного
момента динамической модели

и приведенной силы динамической модели
 Запишем
для них уравнение изменения кинетической
энергии. Кинетическая энергия:
Запишем
для них уравнение изменения кинетической
энергии. Кинетическая энергия:
для механической системы

 для модели
для модели
![]() или
или
![]() Приведенной
массой mnр
– будет некоторая условная масса,
сосредоточенная в точке п, кинетическая
энергия которой в каждом рассматриваемом
положении равна кинетической энергии
всех его звеньев:
Приведенной
массой mnр
– будет некоторая условная масса,
сосредоточенная в точке п, кинетическая
энергия которой в каждом рассматриваемом
положении равна кинетической энергии
всех его звеньев:
 Приведенным
моментом инерции Inр
называется момент инерции, вращающийся
вместе со звеном 1, кинетическая энергия
которого в каждой рассматриваемом
положении механизма равна сумме
кинетических энергий всех звеньев.
Приведенным
моментом инерции Inр
называется момент инерции, вращающийся
вместе со звеном 1, кинетическая энергия
которого в каждой рассматриваемом
положении механизма равна сумме
кинетических энергий всех звеньев.

26) Критерии работоспособности и угол давления при передаче движения в высшей кинематической паре.
Угол
давления
![]() определяет
положение нормали п-п
в высшей КП относительно вектора скорости
и контактной точки ведомого звена. Его
величина определяется размерами
механизма, передаточной функцией
определяет
положение нормали п-п
в высшей КП относительно вектора скорости
и контактной точки ведомого звена. Его
величина определяется размерами
механизма, передаточной функцией
![]() и перемещения толкателя S.
Угол
передачи движения
γ
-
угол между векторами υ2
и υотн
абсолютной и относительной скоростей
той точки толкателя, которая находится
в точке контакта:
и перемещения толкателя S.
Угол
передачи движения
γ
-
угол между векторами υ2
и υотн
абсолютной и относительной скоростей
той точки толкателя, которая находится
в точке контакта:
![]() .
.
Если пренебречь силой трения между кулачком и толкателем, то силой, приводящей в движение толкатель, является давление Q кулачка, приложенное к толкателю в точке и направленное по общей нормали п-п к профилям кулачка и толкателя. Разложим силу Q на взаимно перпендикулярные составляющие Q1 и Q2, из которых первая направлена по направлению скорости υ2. Сила Q1 перемещает толкатель, преодолевая при этом все полезные и вредные сопротивления, приложенные к толкателю. Сила Q2 увеличивает силы трения в кинематической паре, образованной толкателем и стойкой. Очевидно, что с уменьшением угла γ сила Q1 уменьшается, а сила Q2 увеличивается. При некотором значении угла γ может оказаться, что сила Q1 не сможет преодолеть все сопротивления, приложенные к толкателю, и механизм не будет работать. Такое явление называют заклиниванием механизма, а угол γ, при котором оно имеет место, называют углом заклинивания γзакл . При проектировании кулачкового механизма задают допускаемое значение угла давления доп , обеспечивающее выполнения условия γ ≥ γ min > γ закл , т. е. текущий угол γ ни в одном положении кулачкового механизма не должен быть меньше минимального угла передачи γ min и значительно превосходить угол заклинивания γзакл . Для кулачковых механизмов с поступательно движущимся толкателем рекомендуется γ min = 60° и γmin = 45° - механизмов с вращающимся толкателем.
27). Уравнения движения динамической модели
Уравнение движения динамической модели в интегральной форме.
Запишем для динамической модели теорему об изменении кинетической энергии
![]() где:
где:
![]()
![]()

и уравнение движения динамической модели в интегральной или энергетической форме
![]() -
-![]() =
=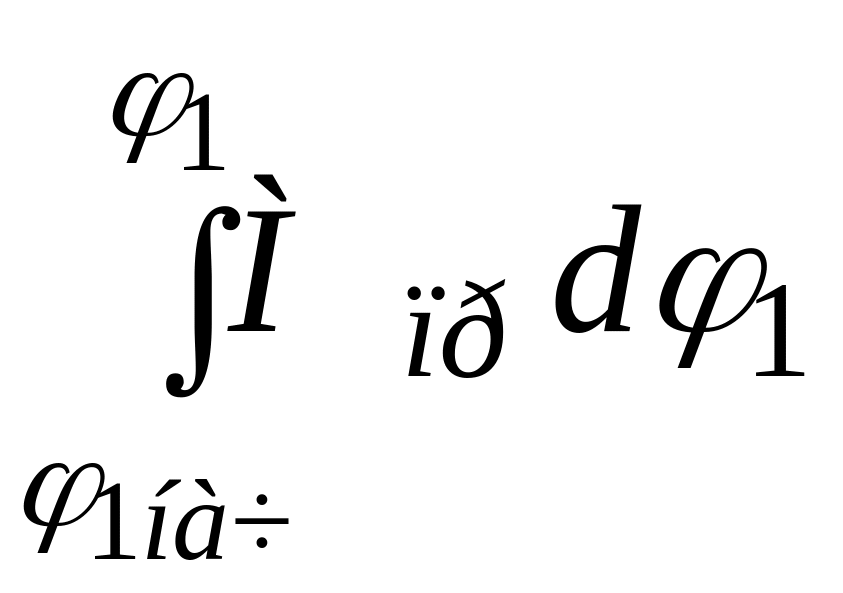
![]()
Из этого уравнения после преобразований получим формулу для расчета угловой скорости звена приведения:

