Тема 4. Кінематичний аналіз механізмів

4.1. Задачі

Визначити закон руху ланок механізму за його кінематичною схемою та законом руху початкової ланки.

Закон руху ланок при різних видах руху визначається рівняннями:

• при поступальному русі:

- переміщення;	(4.1)
- швидкість;
- прискорення.

• при обертальному русі:

  - кутове переміщення;	(4.2)
  - кутова швидкість;
  - кутове прискорення.

• при плоскопаралельному русі:

(4.3)

4.2. Аналоги швидкостей і прискорень

4.2.1. Аналоги швидкостей

Іноді простіше і легше брати похідні не за часом, а за узагальненою координатою, а потім брати похідну за часом від функції узагальненої координати.

Відомо, що швидкість – це перша похідна за часом від радіуса-вектора:

(4.4)

Аналог швидкості:

(4.5)

Аналогічно:

- кутова швидкість;		(4.6)
- аналог кутової швидкості.	(4.7)

Аналог швидкості - це перша похідна від радіуса-вектора за узагальненою координатою, яка може бути як кутовою (j), так і лінійною (S).

Встановимо зв'язок між швидкістю та аналогом швидкості:

-

(4.8)

зв'язок між швидкістю та аналогом швидкості.

Аналогічно:

-

(4.9)

зв'язок між кутовою швидкістю та аналогом кутової швидкості.

Мають розмірність: [м], [1].

4.2.2. Аналоги прискорень

Відомо, що прискорення - це друга похідна за часом від радіуса-вектора.

- лінійне прискорення;	(4.10)
- аналог прискорення.	(4.11)

За аналогією:

- кутове прискорення;	(4.12)
- аналог кутового прискорення.	(4.13)

Аналог прискорення – це друга похідна від радіуса-вектор за узагальненою координатою.

Встановимо зв'язок між прискоренням та аналогом прискорення:

Отже,

.

(4.14)

Аналогічно:

.

(4.15)

Мають розмірність: [м]; [1].

4.3. Методи кінематичного дослідження механізмів (загальна характеристика)

4.3.1. Графічні

Є найбільш розвинутими. Позитивні якості: наочні, відносно прості. Недоліки: не завжди достатньо точні.

4.3.2. Аналітичні

Є більш сучасними. Позитивні якості: точні. Недоліки: громіздкі та складні без застосування ЕОМ.

4.3.3. Експериментальні

Позитивні якості: найбільш вірогідні. Недолік: велика вартість.

4.4 Плани положень механізму

План положень – це зображення кінематичної схеми механізму, що відповідає певному положенню його початкової ланки.

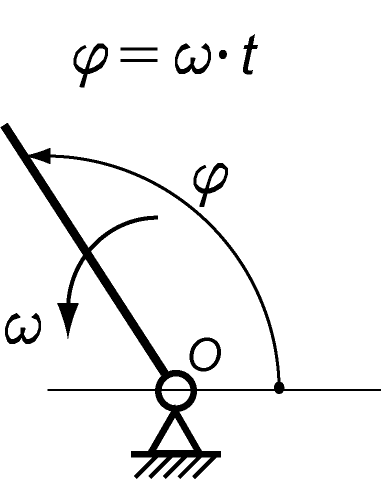
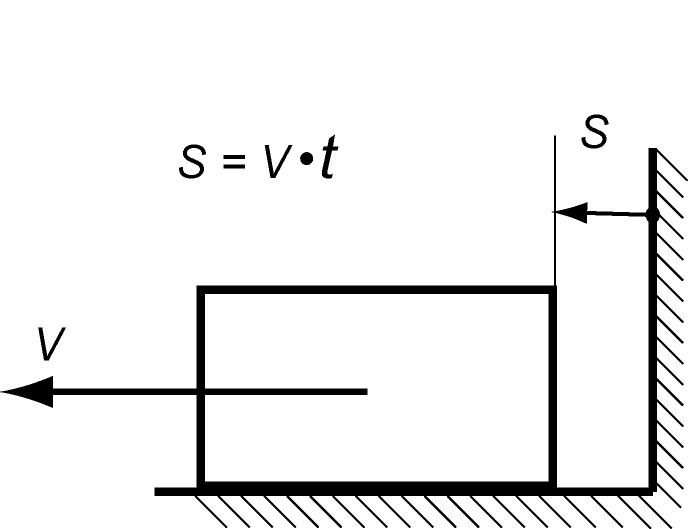
За початкову ланку, зазвичай, приймають кривошип (рис. 4.1) або повзун (рис. 4.2)

Закон руху початкової ланки – функція положення.

Положення решти ланок визначають “методом засічок”, який побудовано на тому положенні ТММ, що всі ланки є абсолютно жорсткими та не змінюють своїх розмірів.

Отже, знаючи траєкторії точок ланок механізму, можна визначити положення будь-якої точки ланки в будь-який момент часу “засічкою”, тобто розхилом циркуля на певну довжину ланки.

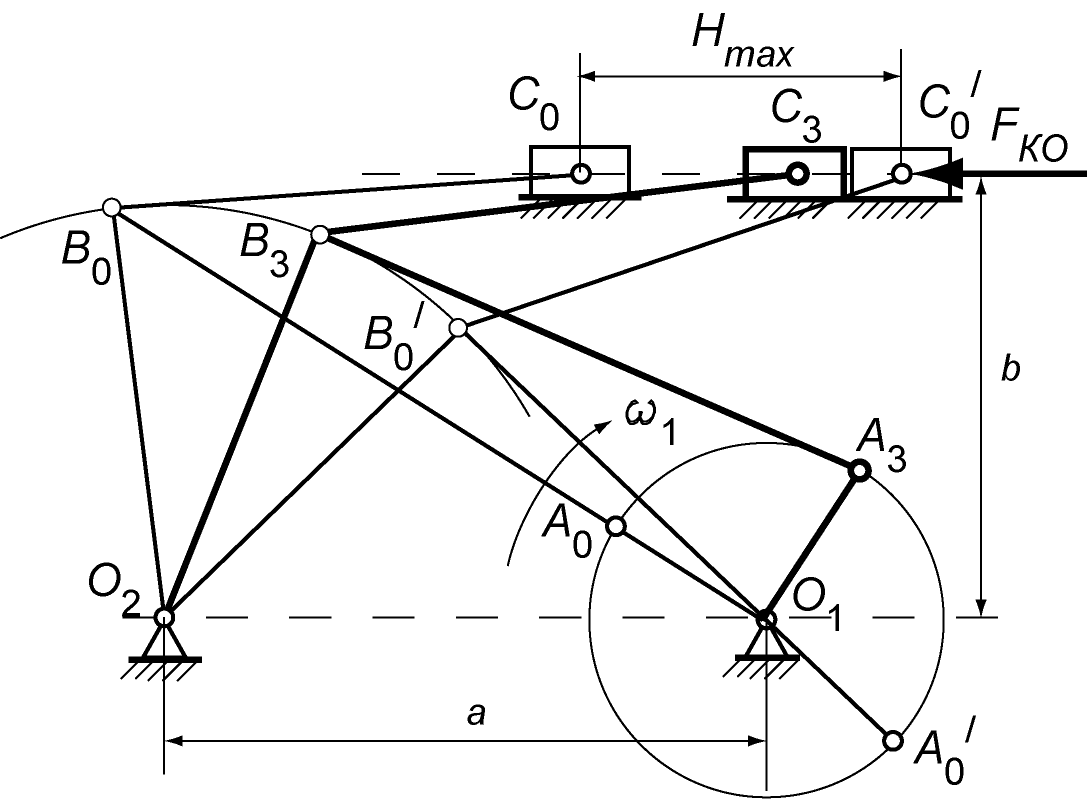
Розглянемо приклад уже вибраного раніше ШВМ завантажника

(рис. 4.3):

Рис. 4.1. Початкова ланка - кривошип	Рис. 4.2 Початкова ланка – повзун
Рис. 4.3. Плани положень механізму