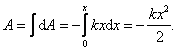13. Работа и энергия. Мощность.

Работа – это скалярная величина.

[A]= Дж

Энергия – это физическая величина, характеризующая способность тела совершать работу.[Е]= Дж

Любое тело обладает скоростью и обладает кинетической энергией:

Потенциальная энергия:

Мощность – это скорость выполнения работы

[N] = Вт

13. Консервативные силы. Потенциальные поля.

Консервативные силы – при действии которых на систему ее механической энергии сохраняется такие силы характеризуются тем, что их работа не зависит от формы траектории, а определяется только начальными и конечным положение точки. Работа таких сил по замкнутой траектории = 0.

Консервативные силы:

Диссипативные силы:

Поле, в котором действуют консервативные силы называется потенциальным полем.

13. Потенциальная энергия. Связь силы и потенциальной энергии.

Потенциальная энергия— скалярная физическая величина, характеризующая способность некоего тела совершать работу за счет его нахождения в поле действия сил. E_п = mgh, [E] = Дж.

Связь между потенциальной энергией и силой 

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

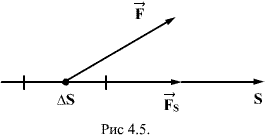
Для установления этой связи вычислим элементарную работу ∆А, совершаемую силами поля при малом перемещении ∆S тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой S. Эта работа равна

∆А=F_sdS

где F_s- проекция силы  на направление S.

 

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии W_x’, она равна убыли потенциальной энергии –W_x’ на отрезке оси ∆S:

∆А=–W_x’

Из двух последних выражений получаем

F_sdS=–W_x’

Откуда

Последнее выражение дает среднее значение F_s на отрезке ∆S. Чтобы получить значение F_s в точке нужно произвести предельный переход:

Так как W_x’ может изменяться не только при перемещении вдоль оси S, но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от W_x’ по S:

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

в математике вектор ,

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом . Следовательно, сила равна градиенту потенциальной энергии, взятого с обратным знаком    

13. Силы в механике. Упругая сила.

В современной физике различают четыре вида взаимодействий:

1. Гравитационное (взаимодействие, обусловленное всемирным тяготением)

2. Электромагнитное (осуществляется через электрические и магнитные поля)

3. Сильное или ядерное (обеспечивает связь частиц в атомном ядре)

4. Слабое (ответственное за многие процессы распада элементарных частиц)

В рамках классической механики имеют дело с гравитационными и электромагнитными силами, а так же с упругими силами и силами трения. Два последних вида сил определяются характером взаимодействия между молекулами вещества. Силы взаимодействия между молекулами имеют электромагнитное происхождение. Следовательно, упругие силы и силы трения являются по своей природе электромагнитными. Гравитационный и электромагнитные силы являются фундаментальными – их нельзя свести к другим, более простым, силам. Законы фундаментальных сил чрезвычайно просты. Гравитационная сила определяется формулой , сила, с которой взаимодействуют два покоящихся точечных заряда и , дается законом Кулона . Если заряды движутся, то кроме кулоновской формулы, на них так же распространяются магнитные силы. Магнитная сила, действующая на точечный заряд q, движущийся со скоростью в магнитном поле с индукцией B, определяется формулой . Выше перечисленные формулы являются точными.

Упругие силы. Всякое реальное тело под действием приложенных к нему сил деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого конкретного тела предел (предел упругости) Рассмотрим упругие деформации. В деформированном теле возникают упругие силы, уравновешивающие внешние силы. Под действием внешней силы –  F_вн  пружина получает удлинение  x, в результате в ней возникает упругая сила –  F_упр, уравновешивающая  F_вн.

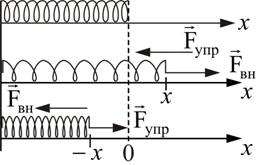
       Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости  F_упр.

       Удлинение пружины пропорционально внешней силе и определяется законом Гука:

k  – жесткость пружины. Видно, что чем больше  k, тем меньшее удлинение получит пружина под действием данной силы. Так как упругая сила отличается от внешней только знаком, т.е.  F_упр = –F_вн, закон Гука можно записать в виде

, F_упр = –kx.

       Потенциальная энергия упругой пружины равна работе, совершенной над пружиной.        Так как сила непостоянна, элементарная работа  dA = F dx, или

dA = –kx dx.

       Тогда полная работа, которая совершена пружиной, равна: