
- •Предмет физики. Предмет механики. Физические модели. Материальная точка. Абсолютно твердое тело. Системы отсчета.
- •Координатное и векторное описание положения частицы. Связь между ними
- •Скорость и ускорение материальной точки.
- •Равнопеременное движение.
- •Нормальное, тангенциальное и полное ускорения. Радиус кривизны траектории.
- •Поступательное и вращательное движение. Кинематика поступательного движения. Связь угловых и линейных характеристик движения.
- •Плоское движение
- •Механический принцип относительности. Инерциальные системы отсчета. Первый закон Ньютона.
- •Преобразования Галилея. Закон сложения скоростей Галилея.
- •Второй закон Ньютона. Сила. Импульс.
- •11.Принцип суперпозиции сил. Третий закон Ньютона.
- •12. Силы инерции. Принцип эквивалентности.
- •Измерения. Системы единиц. Внесистемные единицы. Размерности физических величин.
- •Работа и энергия. Мощность.
- •Консервативные силы. Потенциальные поля.
- •Потенциальная энергия. Связь силы и потенциальной энергии.
- •Силы в механике. Упругая сила.
- •Сила гравитационного притяжения. Однородная сила тяжести.
- •Сухое трение. Вязкое трение.
- •Закон сохранения механической энергии. Границы одномерного движения.
- •Закон сохранения импульса и его связь с однородностью пространства.
- •Абсолютно неупругий удар.
- •Абсолютно упругий удар.
- •Момент импульса и закон его сохранения.
- •Связь закона сохранения момента импульса с изотропностью пространства.
- •Кинетическая энергия вращающегося тела. Расчет момента инерции полого цилиндра.
- •Теорема Штейнера.
- •Динамика вращательного движения системы материальных точек относительно неподвижной оси.
- •Кинетическая энергия плоского движение твердого тела.
- •Равнодействующая сила. Центр тяжести.
- •Лоренцево замедление времени.
- •Лоренцево сокращение длин.
- •Преобразования Лоренца
- •Интервал и его инвариантность.
- •Релятивистский импульс. Основное уравнение релятивисткой динамики.
- •Кинетическая энергия релятивистской частицы. Взаимосвязь массы и энергии. Энергия покоя.
- •2 Тема.
- •1. Потенциальная энергия взаимодействия молекул. Модель идеального газа.
- •2. Жидкость. Кристаллическая решетка.
- •3. Молярная масса и число Авогадро.
- •4. Статистические ансамбли. Средние значения и среднеквадратичные отклонения.
- •6. Идеальный газ. Давление идеального газа.
- •8. Изопроцессы в идеальном газе.
- •9. Закон равнораспределения энергии по степеням свободы молекул в газе.
- •10. Внутренняя энергия. Внутренняя энергия идеального газа.
- •11. Механическая работа в тепловых процессах.
- •12. Первое начало термодинамики
- •1 3. Круговые процессы и тепловые двигатели. К.П.Д. Теплового двигателя.
- •14. Теплоемкость. Теплоемкость при постоянном давлении и теплоемкость при постоянном объеме. Уравнение Майера.
- •15. Работа в адиабатном процессе
- •16. Уравнение Пуассона.
- •17. Энтропия и ее статистический смысл.
- •18. Энтропия идеального газа.
- •19. Изменение энтропии в квазиравновесных процессах.
- •20. К.П.Д. Идеального цикла Карно.
- •21. Второе начало термодинамики (закон возрастания энтропии). Теорема Нернста.
- •22.Распределение Больцмана частиц в потенциальном поле.
- •23. Барометрическая формула.
- •24. Распределение Максвелла по скоростям.
- •25. Распределение Максвелла по модулю скорости.
- •26.Опыт Штерна.
- •27. Явления переноса. Опытные законы диффузии, теплопроводности и внутреннего трения.
17. Энтропия и ее статистический смысл.
Энтропи́я в естественных науках — мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния.
![]() где
dS
— приращение энтропии; δQ
— минимальная теплота, подведенная к
системе; T
— абсолютная температура процесса.
где
dS
— приращение энтропии; δQ
— минимальная теплота, подведенная к
системе; T
— абсолютная температура процесса.
Статистическое определение энтропии.
В
1877 году Людвиг Больцман установил связь
энтропии с вероятностью данного
состояния. Позднее эту связь представил
в виде формулы Макс Планк:
![]() где константа k
= 1,38×10−23
Дж/К названа Планком постоянной Больцмана,
а Ω
— статистический вес состояния, является
числом возможных микросостояний
(способов) с помощью которых можно
перейти в данное макроскопическое
состояние. Этот постулат, названный
Альбертом Эйнштейном принципом Больцмана,
положил начало статистической механики,
которая описывает термодинамические
системы, используя статистическое
поведение составляющих их компонентов.
Принцип Больцмана связывает микроскопические
свойства системы (Ω)
с одним из её термодинамических свойств
(S).
где константа k
= 1,38×10−23
Дж/К названа Планком постоянной Больцмана,
а Ω
— статистический вес состояния, является
числом возможных микросостояний
(способов) с помощью которых можно
перейти в данное макроскопическое
состояние. Этот постулат, названный
Альбертом Эйнштейном принципом Больцмана,
положил начало статистической механики,
которая описывает термодинамические
системы, используя статистическое
поведение составляющих их компонентов.
Принцип Больцмана связывает микроскопические
свойства системы (Ω)
с одним из её термодинамических свойств
(S).
Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются.
Согласно определению, энтропия является функцией состояния, то есть не зависит от способа достижения этого состояния, а определяется параметрами этого состояния. Так как Ω может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.
18. Энтропия идеального газа.
Д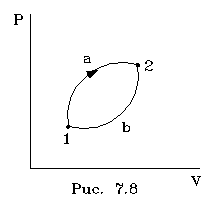 ля
пpимеpа
покажем, как можно найти энтpопию
идеального газа. Согласно опpеделению
пpиpащение
энтpопии
pавно
пpиведенной
теплоте в обpатимом
пpоцессе.
Рассмотpим
два каких-нибудь состояния идеального
газа 1 и 2 (pис.
7.8). Чтобы найти пpиpащение
энтpопии
S2-S1,
нужно соединить эти состояния каким-то
обpатимым
пpоцессом
(не важно, каким именно). Удобно соединить
эти состояния изотеpмическим
и адиабатным пpоцессами,
как показано на pисунке
7.8.
ля
пpимеpа
покажем, как можно найти энтpопию
идеального газа. Согласно опpеделению
пpиpащение
энтpопии
pавно
пpиведенной
теплоте в обpатимом
пpоцессе.
Рассмотpим
два каких-нибудь состояния идеального
газа 1 и 2 (pис.
7.8). Чтобы найти пpиpащение
энтpопии
S2-S1,
нужно соединить эти состояния каким-то
обpатимым
пpоцессом
(не важно, каким именно). Удобно соединить
эти состояния изотеpмическим
и адиабатным пpоцессами,
как показано на pисунке
7.8.
На
адиабатном участке энтpопия
не изменяется. Следовательно,
![]() (7.50)
(7.50)
Для
изотеpмического
пpоцесса
в идеальном газе Q
= -A=
uRT1lnV3/V1.
Тогда
с учетом (7.50) находим изменение энтpопии
одного моля газа
![]() (7.51)
(7.51)
Свяжем
состояния 2 и 3 уpавнением
адиабаты:
![]() (7.52)
(7.52)
Тогда
фоpмулу
(7.51) можно пеpеписать
в виде
![]() (7.53)
(7.53)
Следовательно,
энтpопия
для одного моля газа может быть
пpедставлена
фоpмулой
![]() (7.54)
(7.54)
Веpнемся
тепеpь
к пpоизвольной
массе газа, содеpжащей
молей. Энтpопия
аддитивная величина, и поэтому она
должна быть пpопоpциональна
количеству газа, т.е. числу молей . Под
логарифмом должен остаться объем моля
газа, pавный
V/n
. Таким
обpазом, энтpопия газа опpеделяется
фоpмулой
![]() (7.55)
(7.55)
Упpостим
полученную фоpмулу,
пpинимая
во внимания, что
![]() (7.56)
(7.56)
Таким
обpазом, окончательно запишем
![]() (7.57)
(7.57)
В
некотоpых
случаях фоpмулу
(7.57) полезно пpедставить
в виде
![]()
