15. Работа в адиабатном процессе

Адиабати́ческий — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.

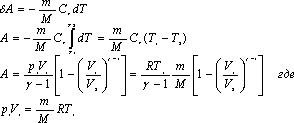
Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок dh совершать работу где F — сила, с которой газ действует на поршень. Перепишем уравнение: где s — площадь поршня. Тогда работа будет равна где — давление газа, dV — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки dS на которых расширение одинаково.

Основное уравнение термодинамики примет вид: (1)

Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны скорость должна быть достаточно большой, чтобы можно было пренебречь обменом теплом с окружающей средой и процесс оставался адиабатическим.

Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид: (1а)

где A_i, da_i — дифференциальное выражение для работы, a_i — внешние параметры, которые меняются при совершении работы, A_i — соответствующие им внутренние параметры, которые при совершении малой работы можно считать постоянными. При совершении работы путём сжатия или расширения внутренний параметр — давление. Внешний параметр — объём.

16. Уравнение Пуассона.

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает электростатическое поле, стационарное поле температуры, поле давления, поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: Δφ = f,где Δ — оператор Лапласа или лапласиан, а f — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

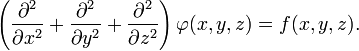
В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид:

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона): Δφ = 0.

Уравнение Пуассона является одним из краеугольных камней электростатики. Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ: где — электростатический потенциал (в вольтах), — объёмная плотность заряда (в кулонах на кубический метр), а — диэлектрическая проницаемость вакуума (в фарадах на метр).

В единицах системы СГС:

В области пространства, где нет непарной плотности заряда, имеем: и уравнение для потенциала превращается в уравнение Лапласа: