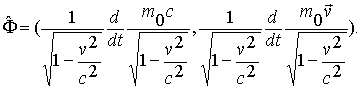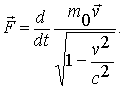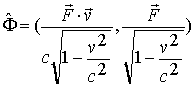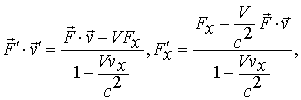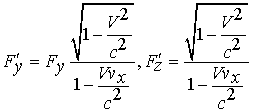- •Предмет физики. Предмет механики. Физические модели. Материальная точка. Абсолютно твердое тело. Системы отсчета.
- •Координатное и векторное описание положения частицы. Связь между ними
- •Скорость и ускорение материальной точки.
- •Равнопеременное движение.
- •Нормальное, тангенциальное и полное ускорения. Радиус кривизны траектории.
- •Поступательное и вращательное движение. Кинематика поступательного движения. Связь угловых и линейных характеристик движения.
- •Плоское движение
- •Механический принцип относительности. Инерциальные системы отсчета. Первый закон Ньютона.
- •Преобразования Галилея. Закон сложения скоростей Галилея.
- •Второй закон Ньютона. Сила. Импульс.
- •11.Принцип суперпозиции сил. Третий закон Ньютона.
- •12. Силы инерции. Принцип эквивалентности.
- •Измерения. Системы единиц. Внесистемные единицы. Размерности физических величин.
- •Работа и энергия. Мощность.
- •Консервативные силы. Потенциальные поля.
- •Потенциальная энергия. Связь силы и потенциальной энергии.
- •Силы в механике. Упругая сила.
- •Сила гравитационного притяжения. Однородная сила тяжести.
- •Сухое трение. Вязкое трение.
- •Закон сохранения механической энергии. Границы одномерного движения.
- •Закон сохранения импульса и его связь с однородностью пространства.
- •Абсолютно неупругий удар.
- •Абсолютно упругий удар.
- •Момент импульса и закон его сохранения.
- •Связь закона сохранения момента импульса с изотропностью пространства.
- •Кинетическая энергия вращающегося тела. Расчет момента инерции полого цилиндра.
- •Теорема Штейнера.
- •Динамика вращательного движения системы материальных точек относительно неподвижной оси.
- •Кинетическая энергия плоского движение твердого тела.
- •Равнодействующая сила. Центр тяжести.
- •Лоренцево замедление времени.
- •Лоренцево сокращение длин.
- •Преобразования Лоренца
- •Интервал и его инвариантность.
- •Релятивистский импульс. Основное уравнение релятивисткой динамики.
- •Кинетическая энергия релятивистской частицы. Взаимосвязь массы и энергии. Энергия покоя.
- •2 Тема.
- •1. Потенциальная энергия взаимодействия молекул. Модель идеального газа.
- •2. Жидкость. Кристаллическая решетка.
- •3. Молярная масса и число Авогадро.
- •4. Статистические ансамбли. Средние значения и среднеквадратичные отклонения.
- •6. Идеальный газ. Давление идеального газа.
- •8. Изопроцессы в идеальном газе.
- •9. Закон равнораспределения энергии по степеням свободы молекул в газе.
- •10. Внутренняя энергия. Внутренняя энергия идеального газа.
- •11. Механическая работа в тепловых процессах.
- •12. Первое начало термодинамики
- •1 3. Круговые процессы и тепловые двигатели. К.П.Д. Теплового двигателя.
- •14. Теплоемкость. Теплоемкость при постоянном давлении и теплоемкость при постоянном объеме. Уравнение Майера.
- •15. Работа в адиабатном процессе
- •16. Уравнение Пуассона.
- •17. Энтропия и ее статистический смысл.
- •18. Энтропия идеального газа.
- •19. Изменение энтропии в квазиравновесных процессах.
- •20. К.П.Д. Идеального цикла Карно.
- •21. Второе начало термодинамики (закон возрастания энтропии). Теорема Нернста.
- •22.Распределение Больцмана частиц в потенциальном поле.
- •23. Барометрическая формула.
- •24. Распределение Максвелла по скоростям.
- •25. Распределение Максвелла по модулю скорости.
- •26.Опыт Штерна.
- •27. Явления переноса. Опытные законы диффузии, теплопроводности и внутреннего трения.
Релятивистский импульс. Основное уравнение релятивисткой динамики.
Выражение,
обеспечивающее инвариантность закона
сохранения импульса, может быть получено,
если вместо времени тау подставить
собственное время t.
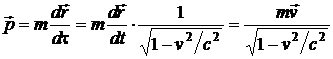 .
.
Основное уравнение релятивистской динамики
В
ньютоновой механике обычная трехмерная
3-сила определяется как скорость изменения
во времени количества движения,
переносимого на данное тело от окружающих
тел и полей (равенство ![]() Ньютона
является одновременно и определением
силы, и законом движения). Аналогично
поступим и в релятивистской механике,
не забывая в то же время, что делить
(множить) следует только на инвариантные
величины. По определению
4-сила
Ньютона
является одновременно и определением
силы, и законом движения). Аналогично
поступим и в релятивистской механике,
не забывая в то же время, что делить
(множить) следует только на инвариантные
величины. По определению
4-сила ![]() -
это скорость изменения 4-импульса,
оцененная в течение собственного времени
движущегося тела (точки; частицы), т.е.
-
это скорость изменения 4-импульса,
оцененная в течение собственного времени
движущегося тела (точки; частицы), т.е. 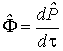 .
Подставляя значение 4-импульса, можно
представить 4-силу в виде
.
Подставляя значение 4-импульса, можно
представить 4-силу в виде
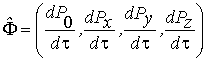
или
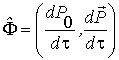
Подставив
значение ![]() и
учтя явный вид компонент импульса
и
учтя явный вид компонент импульса ![]() и
и ![]() ,
получим величину
,
получим величину
|
(1.1) |
Так
выглядит 4-сила в системе I (в которой
время t, скорость ![]() ).
Ниже структура
будет
представлена в более компактном виде.
).
Ниже структура
будет
представлена в более компактном виде.
Здесь
возникает важный вопрос: если при
скоростях значительно меньших скорости
света, т.е. в ньютоновой механике, сила
определяется по второму закону Ньютона
равенством![]() (индекс
"н" указывает на ньютонову механику),
то как следует обобщить понятие 3-силы
на любые скорости, вплоть до как угодно
близких к скорости света?
(индекс
"н" указывает на ньютонову механику),
то как следует обобщить понятие 3-силы
на любые скорости, вплоть до как угодно
близких к скорости света?
Ответ на такие вопросы может давать только практика, эксперименты, опыт. Вся современная экспериментальная физика подтверждает, что под релятивистской 3-силой следует понимать величину, являющуюся производной от релятивистского 3 импульс
|
(1.2) |
Это равенство обобщает ньютонову трактовку 3-силы. В то же время оно представляет основной закон движения частицы (материальной точки) в инерциальной системе отсчета при любыхвозможных скоростях меньших с.
Рассмотрим закон преобразования компонент 4-силы, представленных формулой (8.4). Учитывая (8.5), представим 4-силу в окончательном виде
|
(1.3) |
Как видим, в структуру 4-силы Минковского входит релятивистская
трехмерная
сила
и
ее мощность ![]() .
.
Рассмотрим
дальше преобразование компонент 4-силы
при переходе от ИСО I к ИСО П, которая
движется со скоростью v относительно
системы I в направлении оси х. При этом
в системе I предполагается известным
мгновенное значение скорости
точки ![]() (vx,vy,vz)
и сила
(vx,vy,vz)
и сила ![]() .
Преобразование 4-силы позволит определить
также и величину трехмерной силы в
системе II. Как уже указывалось,
преобразование компонент 3-векторов
определяется на основе сначала
преобразования 4-векторов (при переходе
.
Преобразование 4-силы позволит определить
также и величину трехмерной силы в
системе II. Как уже указывалось,
преобразование компонент 3-векторов
определяется на основе сначала
преобразования 4-векторов (при переходе ![]() ).
Итак, нужно подвергнуть компоненты
4-силы
).
Итак, нужно подвергнуть компоненты
4-силы ![]() ,
т.е.
,
т.е.
|
(1.4) |
преобразованиям Лоренца. Применяя их к (8.7), получим четыре формулы, дающие окончательный вариант преобразований
|
(1.5a) |
|
(1.5b) |
Следовательно,
при переходе от системы отсчет I к системе
II проекции 3-силы ![]() изменяются;
они остаются неизменными в нерелятивистском
случае, когда
изменяются;
они остаются неизменными в нерелятивистском
случае, когда ![]() .
Первая из полученных формул определяет
мощность силы в системе II, остальные
три - проекции силы.
.
Первая из полученных формул определяет
мощность силы в системе II, остальные
три - проекции силы.