2.6 Задача д1. Дифференциальные уравнения движения материальной точки

Груз D массой m, получив в точке A начальную скорость υ₀, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке АВ на груз кроме силы тяжести действуют постоянная сила и сила сопротивления среды , зависящая от скорости груза и направленная против движения.

В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует пе­ременная сила , проекция которой F_x на ось x задана в таблице Д1.

Считая груз материальной точкой и зная расстояние АВ = l или время t₁ движения груза от точки А до точки В, найти закон движе­ния груза на участке ВС в виде функции x = f(t). Трением пренеб­речь.

Таблица Д1 Данные к задаче Д1

Номер условия	m, кг	υ0, м/с	Q, Н	R, Н	l, м	t1, с	Fx, Н
1	2	3	4	5	6	7	8
0	2,4	12	5	0,8υ2	1,5	–	4sin(4t)
1	2	20	6	0,4υ	–	2,5	–5cos(4t)
2	8	10	16	0,5υ2	4	–	6t2
3	1,8	24	5	0,3υ	–	2	–2cos(2t)
4	6	15	12	0,6υ2	5	–	–5sin(2t)
5	4,5	22	9	0,5υ	–	3	3t
6	4	12	10	0,8υ2	2,5	–	6cos(4t)
7	1,6	18	4	0,4υ	–	2	–3sin(4t)
8	4,8	10	10	0,2υ2	4	–	4cos(2t)
9	3	22	9	0,5υ	–	3	4sin(2t)

Пример Д1. На наклонном участке AB трубы на груз D массы m действуют сила тяжести P, сила сопротивления R и сила трения _.; коэффициент трения равен ; время движения груза от точки А, где , до точки В равно ; на вертикальном участке ВС на груз действуют сила тяжести и переменная сила F=F(t), заданная в ньютонах.

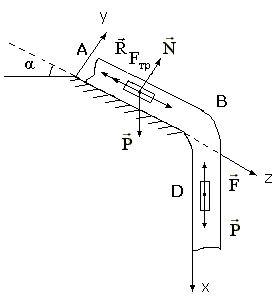
Рис. Д1

Дано: m=2 кг, R = v, где = 0,5 кг/с, f=0,2, v₀=2 м/с , = = 2 c, =30°, .

Определить: закон движения груза на участке ВС, т.е. зависимость .

Указания. Задача — на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке , учтя начальные условия. Затем, зная время движения груза на участке или длину этого участка, определить скорость груза в точке . Эта скорость будет начальной для движения груза на участке . После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке , и полагая в этот момент . При интегрировании уравнения движения на участке в случае, когда задана длина участка, целесообразно перейти к переменному , учтя, что

Решение: Рассмотрим движение груза на участке АВ. Выберем начало отсчета в точке А и направим ось А_z в сторону движения (рис. Д1-1). Тогда начальные условия будут: при . Изображаем в произвольном положении груз и действующие на него силы и (нормальная реакция трубы). Составляем дифференциальное уравнение движения груза в проекции на ось А_z:

или . (1)

Проекции сил имеют значения , .

, , и уравнение (1) примет вид

. (2)

Для определения N составим уравнение в проекции на ось А_y:

или

.

Подставим найденное значение N в уравнение (2) и, разделив обе части уравнения на m, получим:

. (3)

Обозначим и подсчитаем величины:

,

k= 10(0,5 – 0,2×0,866)= 3,27 м/с², (4)

, с^-1.

С учетом (4) уравнение (3) примет вид:

.

Разделяя переменные, запишем:

.

Общее решение данного уравнения есть

(5)

Найдем постоянную интегрирования, используя начальные условия: при t=0, v= v₀

.

Уравнение (5) теперь перепишется в виде:

,

откуда

.

При t=t₁, т.е. в точке В скорость груза равна

м/с.

Рассмотрим теперь движение груза на участке ВС. Выберем начало отсчета в точке В и направим ось В_х вертикально вниз. Будем считать, что при t=0, х=0, v_х= v₁. На груз действуют силы тяжести Р и переменная сила F, зависящая только от t. Дифференциальное уравнение движения груза в проекции на ось В_х имеет вид:

. (6)

Заметим, что в уравнениях (2) и (6) переменные силы выражены через величины, от которых они зависят. Обе стороны уравнения (6) поделим на m и запишем

. (7)

Уравнение (7) дважды последовательно интегрируем и, определяя из начальных условий постоянные интегрирования, находим искомую зависимость х=f(t):

. (8)

При t = 0, , .

Подставляем найденное значение С₂ в (8), получим

откуда

. (9)

При t = 0 C₃ = 0.

Окончательно получим:

.

Подставив числовые значения величин m, g и v₁, получим закон движения груза в виде:

х=2,9t + 5,15t² + 3,5×sint, где t – в с, х – в м.