Раздел 2 Методические указания по изучению содержания тем и разделов дисциплины

2.1 Задача С1. Плоская система сил

Жесткая шарнирная рама (рисунок С1.0 – С1.9) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню в шарнирами на концах, или к шарнирной опоре на катках.

В точке С к раме привязан трос, который перекинут черев блек и несет на конце груз Р = 25 кН. На раму действует пара сил с моментом M = 60 кН*м и две силы, величины, направления и точки приложения которых указаны в таблице С1.

Определить реакции связей в точках А и В, вызываемые действу­ющими нагрузками. При окончательных расчетах принять a = 0,5 м.

Таблица С1 Данные к задаче С1

Силы	α1 F1 = 10 кН		α2 F2 = 20 кН		α3 F3 = 30 кН		α4 F4 = 40 кН
Номер условия	Точка приложения	α1	Точка приложения	α2	Точка приложения	α3	Точка приложения	α4
1	2	3	4	5	6	7	8	9
0	H	30	–	–	K	45	–	–
1	–	–	D	30	H	60	–	–
2	K	75	–	–	–	–	E	30
3	–	–	K	60	H	30	–	–
4	D	30	–	–	–	–	K	60
5	–	–	H	30	D	75	–	–
6	–	–	E	45	–	–	K	30
7	–	–	D	60	H	30	–	–
8	K	60	–	–	–	–	E	45
9	–	–	K	75	–	–	H	30

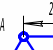
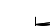
Пример С1 Жесткая шарнирная рама АНСВ (рисунок С1) имеет в точке А шарнирную опору, а в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

Дано: а=0,5м; F₂=20кН; F₄=40кН; M=60кНм, Р=25кН

Определить: реакции связей в точках А и В, вызываемые действующими нагрузками.

Решение.1. Рассмотрим равновесие рамы. Проведем координатные оси xy и изобразим действующие на пластину силы: силу F, пару сил с моментами М, натяжение троса Т и реакции связей XА, YА, RВ (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

Рис.С1

2. Для полученной плоскости системы сил составим три уравнения равновесия. При вычислении момента силы F относительно токи А воспользуемся теоремой Вариньона, т.е. разложим силу F на составляющие.

Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

2.2 Задача С2. Пространственная система сил

Найти реакции опор заданной конструкции. Необходимые для вычислений значения сил Q, G и размеров взять из таблицы С2.

Таблица С2 Данные к задаче С2

Номер условия	Q, H	G, H	a, м	b, м	c, м	R, м	r, м
0	200	100	0,2	0,3	0,1	0,15	0,08
1	300	150	0,3	0,2	0,15	0,18	0,1
2	400	250	0,25	0,2	0,15	0,15	0,07
3	350	200	0,3	0,25	0,2	0,1	0,07
4	250	150	0,25	0,15	0,15	0,12	0,08
5	250	200	0,2	0,25	0,15	0,12	0,07
6	400	300	0,3	0,3	0,2	0,2	0,12
7	150	250	0,2	0,25	0,15	0,12	0,08
8	200	150	0,25	0,2	0,1	0,12	0,1
9	350	300	0,2	0,25	0,15	0,15	0,1

Пример С2 Заданная однородная прямоугольная плита весом G=150Н и силой Q=250H, со сторонами a=0,25м, b=0,15м, закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СD.

Определить реакции опор в точках А и В, и стержне СD

Размеры указаны на чертеже.

Дано: G=150Н, Q=250H, a=0,25м, b=0,15м,.

Решение 1. Рассмотрим равновесие плиты. На нее действуют заданные силы G, Q, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие XA, YА, ZА, цилиндрического (подпятника) – на две составляющие XВ, ZВ, и реакцию Rc стержня направив вдоль стержня, предлагая , что он сжат.

2. Для определения шести неизвестных реакций составим шесть уравнений равновесия действующей на плиту пространственной системы сил:

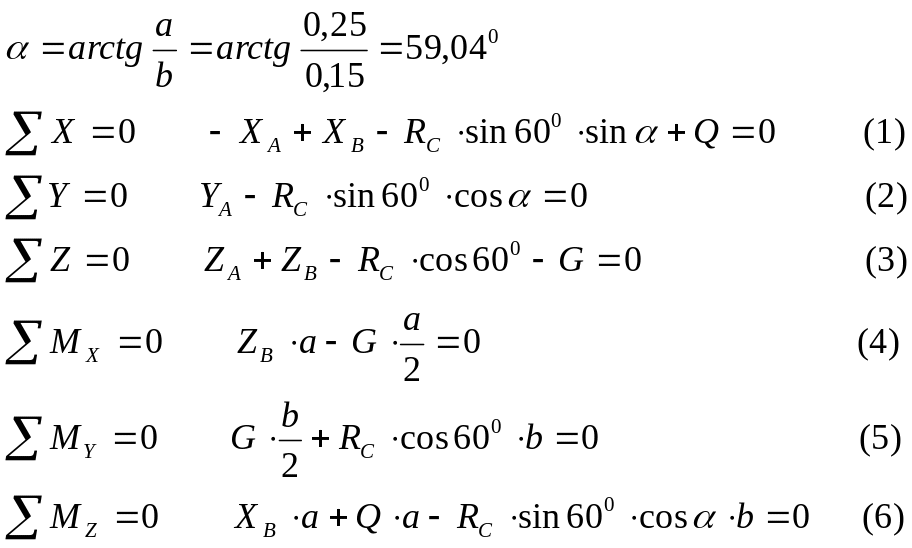
Рис.2

Находим неизвестные из уравнений

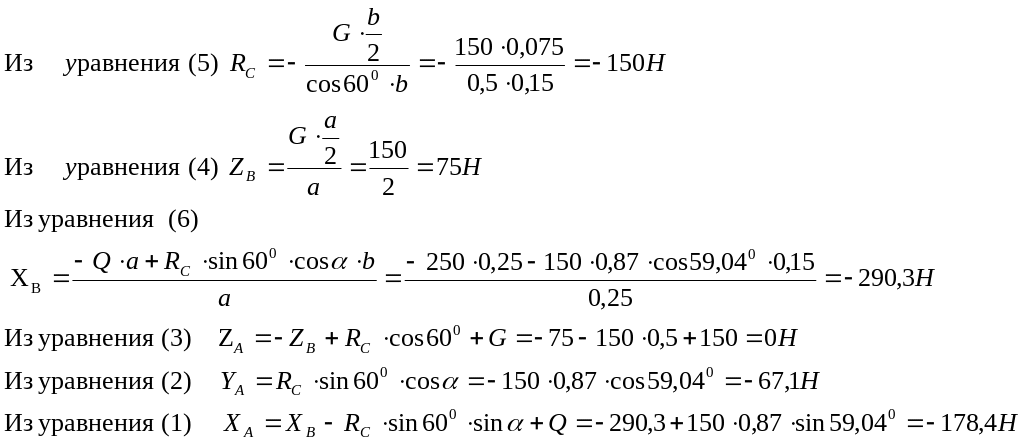
2.3 Задача К1. Кинематика точки

Точка М движется в плоскости xy согласно заданным уравнениям x = x(t) и y = y(t) (таблица К1), где x и y выражены в сантиметрах, t – в секундах.

Найти уравнение траектории точки; для момента времени t₁ = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Построить в масштабе чертеж траектории, указать положение точки М и все вектора.

Таблица К1 Уравнения движения точки М по осям координат

Предпоследняя цифра шифра	х = х(t)	Последняя цифра шифра	y = y (t)
0	–2t2 + 3	0	–5t
1	4t2 – 2t + 1	1	3t
2	–3cos(πt/3) + 2	2	4t
3	2sin(πt/3)	3	–2t
4	3t2 + 2	4	2t
5	7sin(πt/6) + 3	5	–3t
6	–3/(t + 2)	6	–4t
7	–4cos(πt/3)	7	5t
8	3t2 + t + 3	8	2t
9	6sin(πt/6) – 2	9	–3t

Пример К1. Даны уравнения движения точки в плоскости xy: , Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени _.

Решение: Для определения уравнения траектории точки исключим из заданных уравнений движения время t.

Скорости точки:

,

,

Модуль скорости:

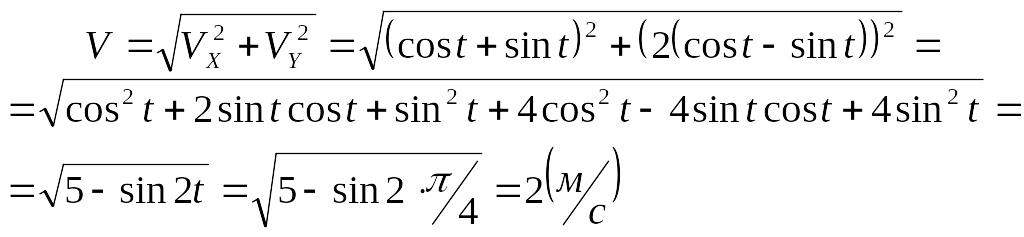
Ускорения точки:

,

,

Модуль полного ускорения:

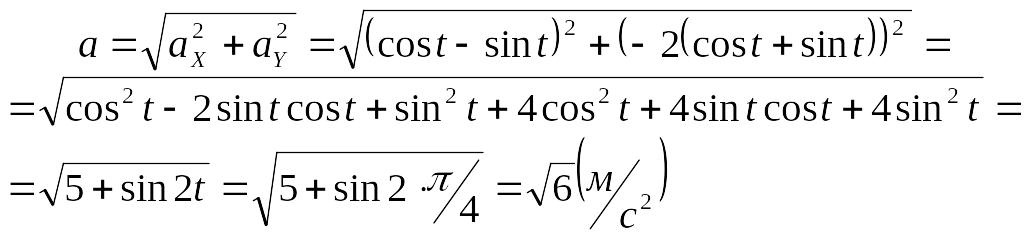
Модуль касательного ускорения точки:

,

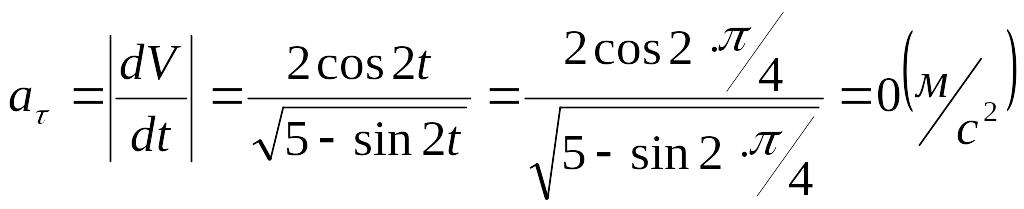А модуль нормального ускорения:

.

Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

2.4 Задача К2. Сложное движение точки. Теорема Кориолиса

Прямоугольная пластина (рисунок К2.0 – К2.4) или круглая пластина радиуса R = 60 см (рисунок К2.5 – К2.9) вращается вокруг неподвижной оси по закону φ = φ(t), заданному в таблице К2. На рисунке 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины, на остальных рисун­ках ось вращения лежит в плоскости пластины.

По пластине вдоль прямой BD (рисунок К2.0 – К2.5) или по окруж–ности (рисунок К2.6 – К2.9) движется точка М; закон ее относительного движения s = AM = s(t) см.

Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t₁ = 1 с.

Таблица К2 Данные к задаче К2

Номер условия	Для всех рисунков φ(t), рад	Для рисунков 0 – 5		Для рисунков 6 – 9
		b, см	s(t)	l	s(t), см
0	4(t2 – t)	12	50(3t – t2) – 64	R	(π/3)R(4t2 – 2t3)
1	3t2 – 8t	16	40(3t2 – t4) – 32	(4/3)R	(π/2)R(2t2 – t3)
2	6t3 – 12t2	10	80(t2 – t) + 40	R	(π/3)R(2t2 – 1)
3	t2 – 2t3	16	60(t4 – 3t2) + 56	R	(π/3)R(t4 – 3t2)
4	10t2 – 5t3	8	80(2t2 – t3) – 48	R	(π/6)R(3t – t2)
5	2(t2 – t)	20	60(t3 – 2t2)	R	(π/3)R(t3 – 2t)
6	5t – 4t2	12	40(t2 – 3t) + 32	(3/4)R	(π/2)R(t3 – 2t2)
7	15t – 3t2	8	60(t – t3) + 24	R	(π/6)R(t – 5t2)
8	2t3 – 11t	10	50(t3 – t) – 30	R	(π/3)R(3t2 – t)
9	6t2 – 3t3	20	40(t – 2t2) – 40	(4/3)R	(π/2)R(t – 2t2)

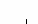
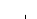
Пример К2. Круглая пластина R = 60 см вращается вокруг неподвижной оси по закону . По дуге окружности R движется точка по закону

Дано: R=60 см; ; l=R; ; t₁= 1 c.

Определить: V_абс и a_абс.

Указания. Задача – на сложное движение точки. Для ее решения следует воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, необходимо по условиям задачи определить, где находится точка М на пластине в момент времени t₁ =1 с, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче).

Решение. Рассмотрим движение точки М как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

,

,

где ,

.

Определим все входящие в равенство величины.

1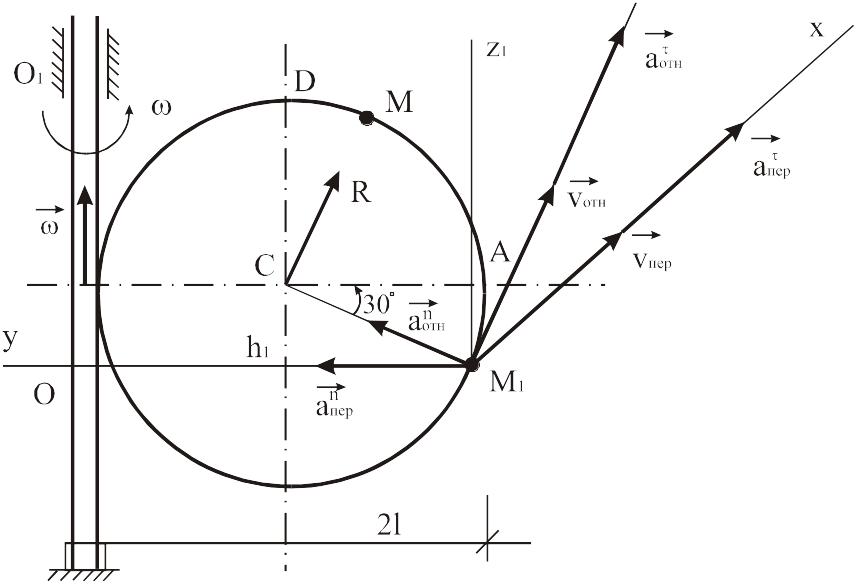 . Относительное движение

Рис.К2

Это движение происходит по закону

.

Установим, где будет находиться точка М на дуге окружности в момент времени t₁, полагая, что t₁ = 1 c:

.

Знак «минус» свидетельствует о том, что точка М в момент времени t₁=1 c находится снизу от точки А. Изображаем ее в этом положении: .

Находим числовые значения , :

м/с.

м/с².

м/с².

Вектор направлен к центру C окружности, векторы и направлены в сторону положительного отсчета.

2. Переносное движение

Это движение происходит по закону .

Найдем сначала угловую скорость и угловое ускорение переносного вращения:

, ,

при t₁ = 1 c, c^-1, c^-2.

Для определения находим сначала расстояние h₁ =О^/М₁ точки М₁ от оси вращения.

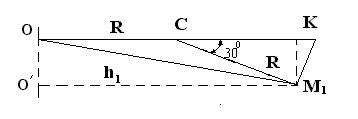
СК =Rcos30⁰ =0,52 м, ОК =СК + R =1,12 м, М₁О^/ = ОК=1,12 м.

Находим: =224 см/с, =448 см/с²,

=448 см/с².

Изобразим векторы и перпендикулярно плоскости DAO^/, а вектор – по линии МO^/ к оси вращения.

3. Кориолисово ускорение

Т.к. угол между вектором и осью вращения (вектором ) равен 30⁰, то численно в момент времени t₁ =1 с

=2·0,31·2·(1/2) =0,68 см/с².

Направление найдем по правилу Жуковского. Для этого вектор спроектируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору ), и затем эту проекцию повернем на 90⁰ в сторону , т.е. против хода часовой стрелки. Получим направление вектора . Он направлен перпендикулярно плоскости пластины так же, как и вектор .

4. Определение V_абс и а_абс Т.к. , а векторы и взаимноперпендикулярны, то

= 234 см/с.

По теореме о сложении ускорений

.

Для определения а_абс проведем координаты М₁хуz и вычислим проекции а_абс на эти оси. Векторы и лежат на оси х, а векторы и расположены в плоскости М₁уz₁, т.е. в плоскости пластины.

Проецируя обе части равенства на оси М₁хуz, получаем:

а_{абс х} = =448,62 см/с²,

а_{абс z} = · =1,71 см/с²,

а_{абс у} = =449,08 см/с².

Находим затем а_абс. а_абс = =634,8 см/с².

Ответ: V_абс =234 см/с; a_абс =634,8 см/с².

2.5 Задача КЗ. Плоскопараллельное движение твердого тела

Для заданного положения механизма найти незаданные угловые скорости и ускорения звеньев механизма, а также скорости и ускорения точек В и С.

Таблица К3 Данные к задаче К3

Номер условия	Размеры, см			ω0, с–1	ε0, с–2
	ОА	АВ	АС
1	2	3	4	5	6
0	50	100	30	4	5
1	40	80	30	3	6
2	35	75	25	–5	7
3	30	70	30	3	6
4	40	100	50	3	–5
5	20	70	30	2	4
6	25	75	25	–3	5
7	40	100	40	3	–5
8	15	50	20	4	6
9	45	120	40	2	–4

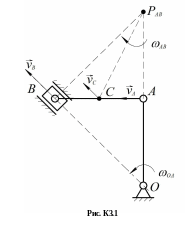
Пример К3. Найти для заданного положения механизма скорости и ускорения точек B и C, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат.

Дано: Cхема механизма в заданном положении (рис.К3.1), исходные данные таковы, что OA = 40 см, AC = 20 см, ω_OA = 5 рад/с, ε_OA = 10 рад/с².

Найти: .

Решение: 1) Определение скорости точек и угловой скорости звена AB: вычисляем модуль скорости точки A при заданном положении механизма:

.

Скорость точки А перпендикулярна кривошипу ОА. Скорость ползуна В направлена вдоль ОВ. Мгновенный центр скоростей P_AB шатуна АВ находится в точке пересечения перпендикуляров, проведенных из точек A и B к их скоростям.

Угловая скорость звена AB:

.

Расстояния АР_АВ, ВР_АВ и СР_АВ определяются из рассмотрения треугольников АСР_АВ и АВР_АВ :

AP_АВ=OA=40 см, ВP_АВ= см, СP_АВ= см.

В соответствии с этим , ; ; .

Вектор направлен перпендикулярно отрезку СР_АВ в сторону, соответствующую направлению вращения звена АВ.

2) Определение ускорений точек и углового ускорения звена AB (рис.К.3.2). Ускорение точки A складывается из вращательного и центростремительного ускорений:

,

где , .

Согласно теореме об ускорениях точек плоской фигуры:

или . (1)

Вектор направлен от A к О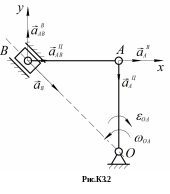 . Вектор перпендикулярен вектору и направлен в сторону, противоположную , (т.к. из условия задачи движение кривошипа OA замедленное).

Центростремительное ускорение точки B во вращательном движении шатуна AB вокруг полюса A: и направлено от B к A.

Ускорение направлено вдоль линии OB, а . Зададим произвольно их направления: - вертикально вверх, - от B к O. Эти ускорения определим из уравнений проекций векторного равенства (2) на оси координат. Знак в ответе показывает, соответствует ли истинное направление вектора принятому при расчете.

Выбрав направление осей x и y, как показано на рис.К3.2, получаем:

, (2)

. (3)

Из уравнения (2) находим

.

Из уравнения (3) получаем

.

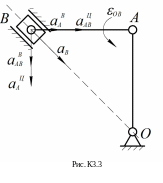
Следовательно, ускорение направлено так, как показано на рисунке, а – в противоположную сторону. Истинная картина ускорений для точки B показана на рис.К.3.3.

Угловое ускорение шатуна AB: .

Направление относительно полюса A определяет направление углового ускорения . В данном случае, не совпадает с направлением , следовательно, движение звена замедленное.

Определим ускорение точки C:

.

Вращательное и центростремительное ускорения точки C во вращательном движении AB вокруг полюса A:

;

.

Вектор перпендикулярен вектору и направлен соответственно угловому ускорению .

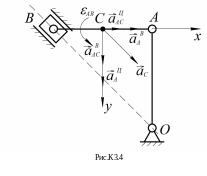
Ускорение находим методом проекций (рис.К3.4):

, ,

.

В результате вычислений получаем:

,

,