10) Естественный (натуральный) трехгранник, вектор ускорения точки при естественном способе задания ее движения. Касательное и нормальное ускорение точки.

При естественном способе задания движения вектор   определяют по его проекциям на оси  , имеющие начало в точке М и движущиеся вместе с нею (рис.8). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось   - вдоль каса­тельной к траектории в сторону положительного отсчета расстояния s; ось   - по нормали, лежащей в соприкасающейся плос­кости и направленной в сторону вогнутости траектории; ось   - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль  , лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная к ней нормаль   - бинормалью.

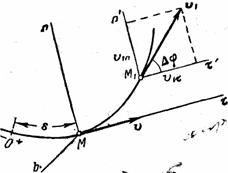
Рис.8

           

Было показано, что ускорение точки   лежит в соприкасающейся плоскости, т.е. в плоскости  ; следовательно, проекция вектора   на бинормаль равна нулю ( ).              

Вычислим проекции  , на две другие оси. Пусть в момент времени t точка находится в положении М и имеет скорость  , a в момент   приходит в положение М1 и имеет скорость  .

Тогда по определению

.

Перейдем в этом равенстве от векторов к их проекциям на оси   и  , проведенные в точке М (рис.8). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:

,   .

Учитывая, что проекция вектора на параллельные оси одинаковы,  проведем через точку М1 оси   параллельные   и обозначим угол между направлением вектора    и касательной   через  . Этот угол между касательными к кривой в точках М и М1 называется углом смежности.

Напомним, что предел отношения угла смежности   к длине дуги   определяет кривизну k кривой в точке М. Кривизна же является величиной, обратной радиусу кривизны   в точке М. Таким образом,

. 

Обращаясь теперь к чертежу (рис.9), находим, что проекции векторов   и   на оси  будут равны:

,

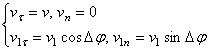где   и   - численные величины скорости точки в моменты   и  .

Следовательно,

.

Заметим что при   точка М1 неограниченно приближается к М и одновременно

.

Тогда, учитывая, что в пределе  , получим для   выражение

.

Правую часть выражения   преобразуем так, чтобы в нее вошли отношения, пределы которых нам известны. Для этого умножим числитель и знаменатель дроби, стоящей под знаком предела, на  . Тогда будем иметь

,

так как пределы каждого из стоящих в скобке сомножителей при   равны:

Окончательно получаем:

.

Итак, мы доказали, что проекция ускорения точки на каса­тельную  равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты)  s noвремени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинор­маль равна нулю ( ). Эти результаты выражают собою одну из важных теорем кинема­тики точки.

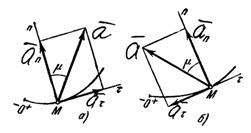
Рис.9

                                                      

Отложим вдоль касатель­ной   и главной нормали   векторы    и  , чис­ленно  равные   и   (рис. 9).  Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая    бу­дет всегда  направлена в сторону вогнутости кривой (величина a всегда положительна),  а составляющая    может быть направлена или в положительном, или в отрицательном направлении оси   в зависимости от знака проек­ции   (см. рис.9, а и б).

Вектор ускорения точки   изображается диагональю параллело­грамма, построенного на составляющих   и  . Так как эти состав­ляющие взаимно перпендикулярны, то по модулю:

.

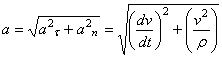Естественный трехгранник (естественные оси координат). Естественным трехгранником называется подвижная прямоугольная система координат, двигающаяся с точкой по траектории. Две оси этой системы координат направлены по единичным векторам касательной и главной нормали к траектории τ и n, а третья ось направлена по вектору b, равному  , который называется единичным вектором бинормали к траектории (рис. 65).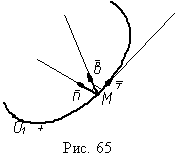

Удобство естественной системы координат состоит в том, что вектор скорости направлен по касательной к траектории, и его проекции на главную нормаль и бинормаль равны нулю. Вектор ускорения лежит в соприкасающейся плоскости, которая, как мы помним, содержит касательную и главную нормаль. Векторы касательного и нормального ускорения направлены по касательной и главной нормали, а поэтому, как и вектор ускорения, на бинормаль не проектируются.

Спроектировав векторы V и a на оси естественного трехгранника, мы можем записать эти векторы в проекциях на естественные оси:

	(16)
	(17)

где

(18)

В выражении (16) Vτ является проекцией скорости на касательную, а в выражении (17) aτ и an - проекции ускорения на касательную и главную нормаль.