2.2.2 Метод простої ітерації

Для розв’язку системи нелінійних рівнянь методом простої ітерації необхідно навести її у виді:

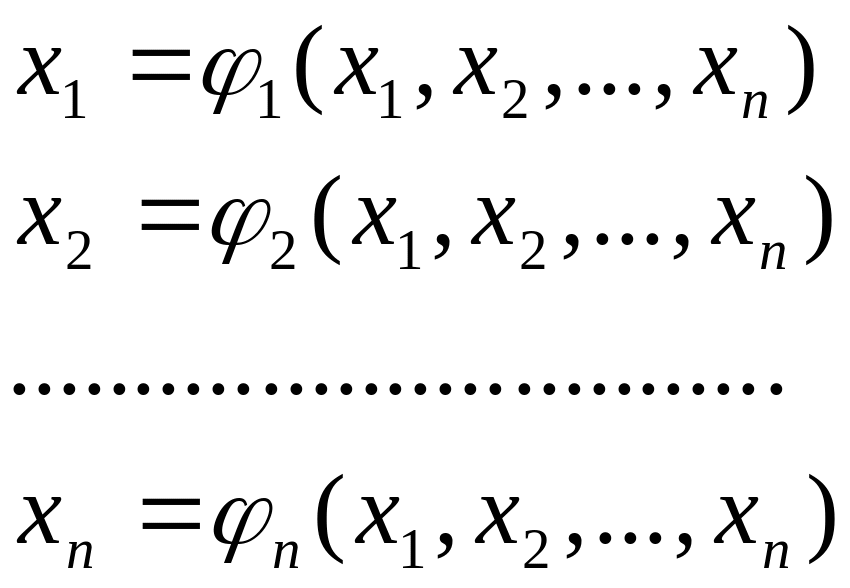(2.9)

Ітераційний процес реалізується наступними формулами:

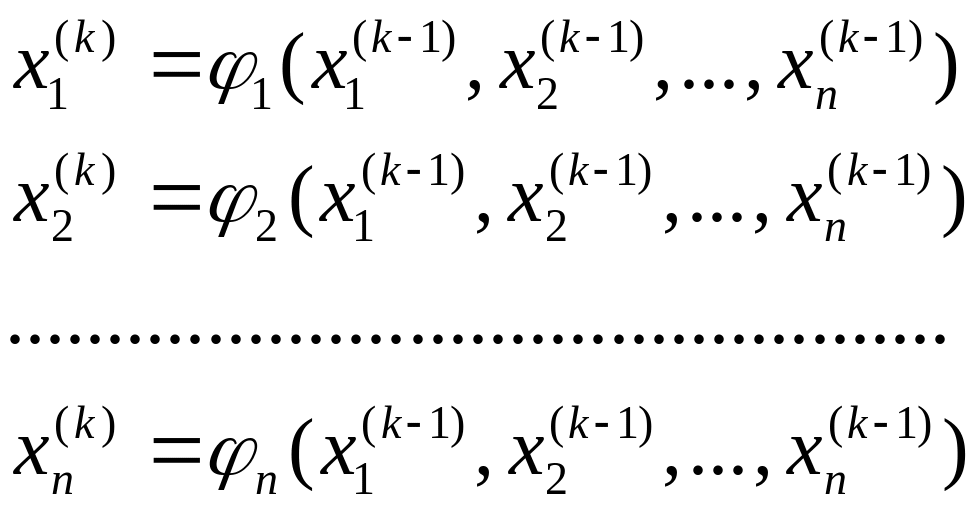(2.10)

Ітераційний процес продовжується доки не буде досягнуте виконання умов (2.11) або (2.12):

• критерій з абсолютних відхилень:

(2.11)

• критерій з відносних відхилень (якщо ):

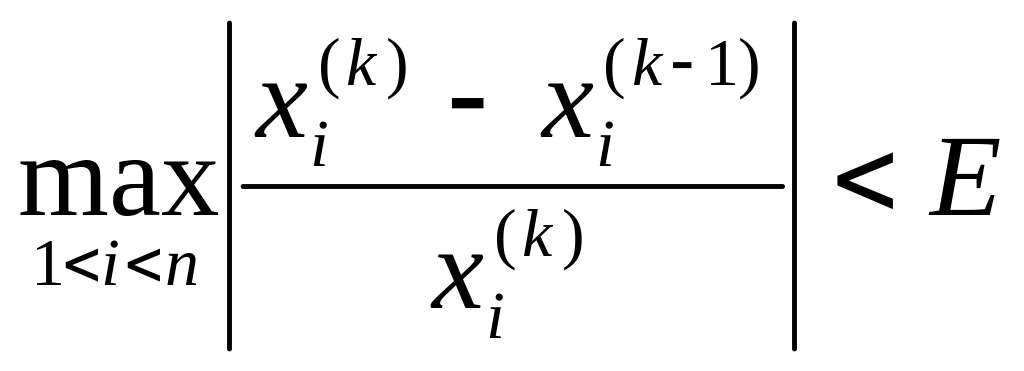(2.12)

де – задана похибка невідомих.

Умова збіжності методу визначається формулою

, (2.13)

де , – перша або друга норма матриці ,

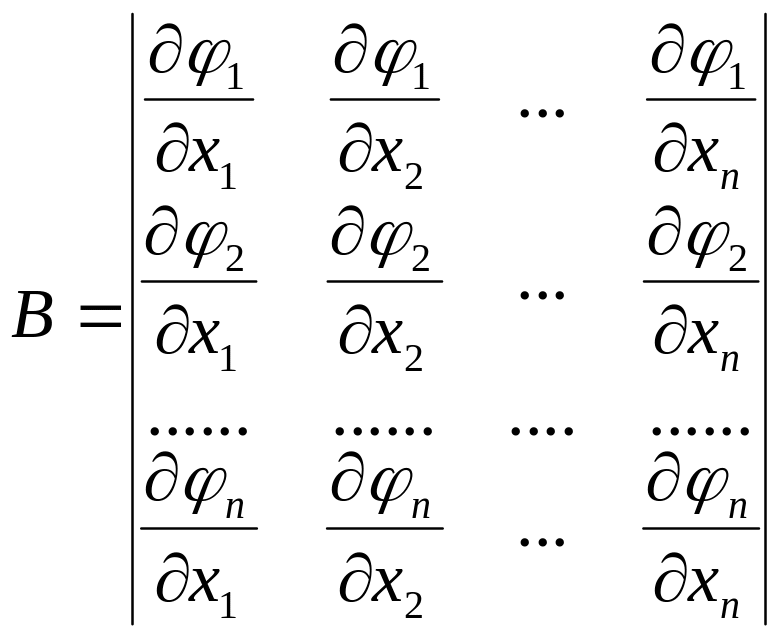(2.14)

матриця частинних похідних правих частин , , системи (2.9), обчислених у точці первинного наближення , , …, .

2.2.3 Метод Зейделя

Метод Зейделя є модифікованим методом простої ітерації, на відміну від якого, уточнені значення коренів відразу підставляються в наступні рівняння.

Послідовні наближення визначаються із співвідношень:

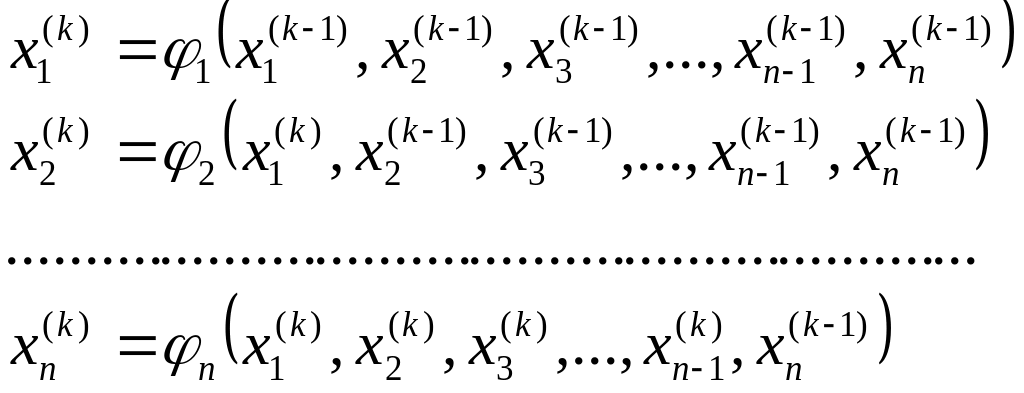(2.15)

Все сказане відносно збіжності методу простої ітерації в п. 2.2.2, вірно і для методу Зейделя, тобто умова збіжності залишається такою самою.

2.3 Завдання

Розв’язати систему нелінійних рівнянь з точністю до .

1) За методом Ньютона отримати систему лінійних рівнянь та розв’язати ії прямим методом з завдання 1.5 п. 1);

2) Розв’язати систему ітераційним методом (ітерацій або Зейделя). Метод вказано в таблиці варіантів;

3) Порівняти результати, отримані за пп. 1) і 2);

4) Навести блок-схеми алгоритмів використаних методів.

№	Система рівнянь	Метод
1.		Простої ітерації
2.		Зейделя
3.		Простої ітерації
4.		Зейделя
5.		Простої ітерації
6.		Зейделя
7.		Простої ітерації
8.		Зейделя
9.		Простої ітерації
10.		Зейделя
11.		Простої ітерації
12.		Зейделя
13.		Простої ітерації
14.		Зейделя
15.		Простої ітерації
16.		Зейделя
17.		Простої ітерації
18.		Зейделя
19.		Простої ітерації
20.		Зейделя
21.		Простої ітерації
22.		Зейделя
23.		Простої ітерації
24.		Зейделя
25.		Простої ітерації
26.		Зейделя
27.		Простої ітерації
28.		Зейделя
29.		Простої ітерації
30.		Зейделя