7. Синтез оптимальных линейных систем управления по интегральному квадратичному критерию и методом фазовой плоскости

В начале 60-х годов различными авторами, в частности Р.Калманом в США, А.М.Летовым в СССР были получены аналитические решения задач об оптимальной стабилизации линейных стационарных и нестационарных систем. Эти работы благодаря ясной постановке задачи и конструктивным результатам инициировали большой поток исследовательских работ по синтезу регуляторов для различных классов систем (линейных и нелинейных, непрерывных и дискретных, с запаздыванием и т.д.), в которых при решении задачи оптимизации управления были решены проблемы краевой задачи метода динамического программирования и принципа максимума. Указанное направление исследований получило название аналитического конструирования или линейно-квадратической оптимизацией. Последнее связано с рассмотрением линейных систем, критерием оптимальности управления которых определен некоторый квадратический функционал.

Однако, видимо, следует под развиваемым направлением понимать не суженную область исследований, упомянутую выше, а всякое аналитическое решение задачи оптимального управления, доведенное до возможности конструктивной реализации с заданной структурой системы управления, которое будем называть синтезом оптимальных систем управления независимо от классов рассматриваемых систем.

Отметим также, что в данном случае мы не будем касаться вопросов, связанных с решением краевой задачи оптимального управления, с определением структуры программного управления системами. Мы будем интересоваться только синтезом замкнутых систем, в которых управление будет определяться как функция координат состояния.

7.1. Синтез нестационарного оптимального управления линейной системой при квадратическом критерии

Рассмотрим задачу синтеза оптимальной системы управления для объекта, описываемого линейной системой

, (7.1)

для которой эффективность управления при переводе системы в конечное состояние описывается критерием вида

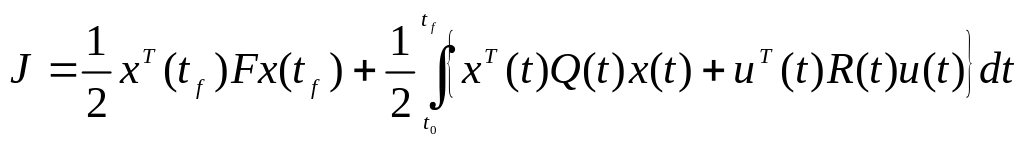. (7.2)

Здесь - n-вектор состояния системы, - начальное состояние системы в момент , - конечное состояние системы в момент окончания процесса , - неотрицательно-определенные матрицы для всего процесса управления (т.е. при и , - положительно-определенная матрица, - некоторое внешнее воздействие). Потребуем также непрерывность .

Задача состоит в отыскании управления с обратной связью , при котором при заданном функционал (7.2) достигает минимума (задача о нестационарном регуляторе).

Очевидно, что к данной задаче применим метод динамического программирования. При этом функция Беллмана принимает вид

, (7.3)

где, используя определение, граничное условие имеет вид

. (7.4)

Соответствующее уравнение Беллмана можно записать следующим образом:

(7.5)

Если предположить, что ограничения на управление и фазовые координаты отсутствуют, то решение в (7.5) достигается во внутренних точках области допустимых управлений и (7.5) можно записать в виде двух уравнений: функционального уравнения и уравнения, вытекающего из необходимого условия экстремума:

(7.6)

(7.7)

Уравнение (7.7) преобразуется, если учесть, что

, ,

к виду

,

откуда можем выразить уравнение для оптимального управления

. (7.8)

Если выражение (7.8) подставить в (7.6), получим уравнение для функции Беллмана (опустив везде аргумент t)

.(7.9)

Из граничного условия (7.4) можем предположить, что искомую функцию Беллмана, которая при имеет квадратичную форму относительно , можно тоже представить в виде функции второго порядка относительно :

, (7.10)

где - симметричная неотрицательно определённая матрица, - векторная функция, - скалярная функция.

Перед подстановкой (7.10) в (7.9) учтем, что по правилам дифференцирования матриц:

, . (7.11)

Если теперь выражения (7.11) подставить в (7.9) с заменой , то получим:

.

Произведём в этой формуле операции транспонирования с учетом правила и раскроем скобки:

(7.12)

В уравнении (7.12) учтем два факта:

1. Слева и справа стоят скаляры, а следовательно должно выполняться и равенство транспонированных выражений, т.к. для скаляра ;

2. Слева и справа стоят «квадратные многочлены» относительно 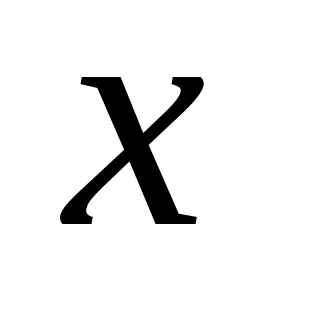и поэтому должны быть равны коэффициенты справа и слева для одинаковых степеней .

Поэтому выполним операцию транспонирования (7.12) с учетом симметричных свойств матриц :

(7.12`)

сложим (7.12) и (7.12`) и сравним коэффициенты при равных степенях

, (7.13)

,(7.14)

. (7.15)

Учитывая замену , из (7.13) - (7.15) получим уравнения:

, (7.16)

, (7.17)

. (7.18)

Начальные условия для , и получим из краевого условия (7.4), откуда следует, что с учетом (7.10)

,

а следовательно:

. (7.19)

Уравнение (7.16) является матричным дифференциальным уравнением с неизвестными коэффициентами вследствие симметричности , уравнение (7.17) - векторным дифференциальным уравнением с неизвестными, а (7.18) является скалярным дифференциальным уравнением. Итого, требуется решить дифференциальных уравнений.

Уравнение (7.16) носит название дифференциального матричного уравнения Риккати, которое аналитически можно решить только в отдельных случаях. Чаще всего систему (7.16) - (7.18), (7.19) решают численными методами на ЭВМ в обратном времени, произведя замену , и тогда, если изменяется от к , то - от до .

Получаемое в результате решения оптимальное управление (7.8) принимает с учетом (7.11) вид

. (7.20)

Если в (7.1) внешнее воздействие отсутствует, т.е. , то уравнение (7.17) принимает вид

, .

Его общее решение имеет структуру

.

Частное решение, удовлетворяющее условию , существует, если , т.е. .

Из (7.18) сразу следует, что в этом случае или . Но условие (7.19) может быть удовлетворено, если , или .

Тогда для отыскания решения задачи оптимального нестационарного управления необходимо решить только уравнение Риккати (7.16) и оптимальное управление принимает вид

(7.21)

или, если ввести коэффициент усиления обратной связи

, (7.22)

получим формулу управления по замкнутому контуру

. (7.23)

Структура нестационарного регулятора представлена на рис 7.1.

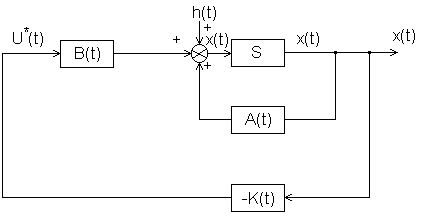
Рис. 7.1. Оптимальный линейный регулятор с обратной связью

Обратим внимание теперь на матрицы , и , элементы которых устанавливаются исследователем в зависимости от условий задачи. Сначала установим причины требований, которые были заявлены в начале раздела по отношению к указанным матрицам.

Для этого вспомним, что необходимым условием экстремума функционала (7.2) являются уравнения Эйлера-Лагранжа, которым удовлетворяет уравнение Беллмана и которые опираются на первую вариацию функционала.

Знак второй вариации, которая равна

,(7.24)

определяет тип экстремума. Так как по условию мы решали задачу минимизации , то для этого нужно, чтобы . Для этого необходимо, чтобы, в силу произвольности вариаций и , матрицы , и были по крайней мере положительно полуопределенными, а так как в силу (7.8) должна быть обращаемой (т.е. ), то она должна быть положительно определенной.

Далее мы должны отметить, что значения элементов матрицы по величине устанавливают исходя из требований к точности достижения системой заданного конечного состояния . Если в пределе , то это значит, что конечные значения фазовых координат состояния могут быть произвольными и наоборот, если некоторые элементы матрицы неограниченно возрастают, то это значит, что независимо от значений интегральной части критерия (7.2), необходимо достичь точных конечных значений соответствующих координат.

Наиболее реалистично матрицу представлять в диагональном виде. Так, если в качестве понимать отклонение от программного движения (т.е. управлять по отклонению), то диагональная матрица обеспечит для первого слагаемого критерия (7.2) вид , который легко интерпретируется как соответствующим образом нормированное отклонение от идеального «попадания» в конечное состояние.

Если некоторые элементы матрицы достаточно велики, что приводит к затруднениям в вычислениях для уравнения Риккати, можно получить «инверсное» дифференциальное уравнение Риккати.

Из тождества после дифференцирования получим

, (7.25)

а умножив (7.16) слева и справа на , имеем

. (7.26)

Используя (7.25) для левой части (7.26), получим “инверсное” уравнение Риккати

(7.27)

с граничными условиями .

Таким образом, можно решить уравнение Риккати так, чтобы была нулевой матрицей, для чего необходимо, чтобы каждая компонента вектора состояния достигала начала в момент достижения границы. «Усиление» или некоторые его компоненты в этом случае в момент достижения границы становятся бесконечными.

Рассматривая следующие слагаемые в критерии управления (7.2), можно заметить, что если все так же считать вектором отклонений, то слагаемое является величиной, пропорциональной квадратической ошибке, и характеризует качество регулирования на всем интервале . Абсолютную величину этого слагаемого по существу и определяет как раз матрица .

Последнее слагаемое в (7.2), квадратичное относительно управляющего воздействия , из физических соображений является пропорциональным «энергетическим» затратам на процесс управления. Матрица определяет абсолютную величину этого слагаемого и поэтому может быть использована для формирования нестрогих ограничений на управление.

Матрицы и в общем случае выбирают зависимыми от времени. Хотя бы из тех соображений, что начальное состояние не зависит от процесса управления. Поэтому желательно исключить влияние начального периода движения системы на величину критерия, настроив так, чтобы вблизи .

Указать однозначно правила выбора элементов и невозможно. На основании большого объема теоретических и экспериментальных исследований специалисты рекомендуют прежде всего брать их диагональными. Это обеспечивает определенный физический смысл слагаемым. Для самих элементов и некоторые авторы рекомендуют величины:

,

.

Для матрицы те же авторы рекомендуют диагональный вид и .

Если в задаче (7.1) - (7.2) конечно, то, независимо от того, являются ли матрицы в (7.1) - (7.2) постоянными или зависящими от времени, эта задача является задачей построения (синтеза) нестационарного регулятора.

Пример 7.1. Для одномерной системы , с критерием выполнить синтез нестационарного регулятора для различных значений .

Решение. Уравнение Риккати (7.16) принимает вид (с учетом 7.19):

, .

Решение его можно записать в виде

,

где вычисляем из условия .

Если, например, и мы не придаем особого значения состоянию в конечный момент, т.е. , то находим из условия , а из (7.22) находим .

Если , то получим график , смещенный по оси при неизменной форме самого коэффициента усиления. На рис. 7.2,а показаны зависимости для обоих случаев.

Если и , то находим из условия . Ошибке в конечной точке придается большое значение и в конечный момент . Для случая происходит смещение графика (рис. 7.2,б).

Если , то воспользуемся инверсным уравнением Риккати (7.27) с соответствующим граничным условием , , откуда , , и графики зависимости представлены на рис. 7.2,в.

а б в

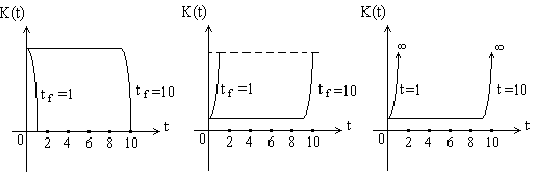
Рис. 7.2. Зависимость коэффициента усиления в различных случаях

Отметим, что решение задачи синтеза оптимального нестационарного линейного регулятора состояния всегда существует, и оно единственно. Кроме того, следует отметить и тот факт, что мы не требовали от системы ее полной управляемости. То есть и для не вполне управляемой системы задача решается. Это связано с тем, что процесс управления рассматривается на конечном интервале времени и вклад неуправляемых координат в значение критерия оптимальности конечен.