2. Взаимное расположение прямой и окружности и двух окружностей.

1. Прямая и окружность:

прямая и окружность прямая касается прямая пересекает

не имеют общих точек окружности окружность

OM – d - расстояние от центра до прямой ( )

OA – r - радиус окружности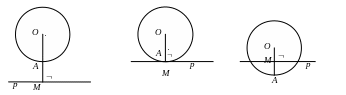

d = r d < r

d > r

32

2. Две окружности:

расстояние между центрами окружностей

R – радиус одной окружности

r - радиус другой окружности

окружности не имеют имеют одну общую имеют две общие

общих точек точку точки (пересекаются)

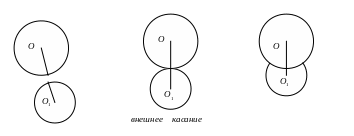
d > R + r d = R + r R – r < d < R + r

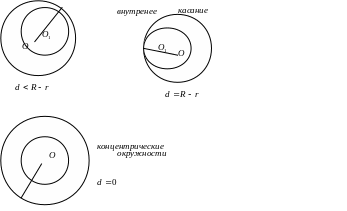
3. Длина окружности и площадь круга.

круг сектор

c =2 π r c = (длина окружности) l =

(длина дуги)

S =π S = (площадь круга) S = (площадь сектора)

сегмент полоса

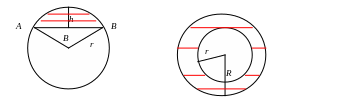
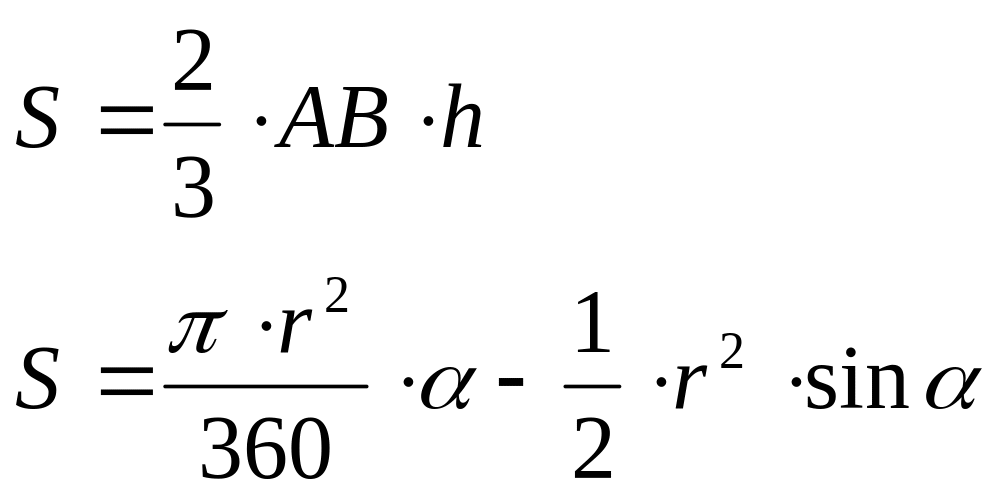
AB –длина хорды сегмента

h- высота сегмента

- центральный угол сегмента

r –радиус сегмента

4. Касательная к окружности.

1). Свойство касательной к окружности: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.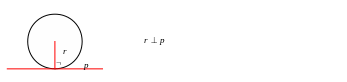

2). Свойство касательных, проведенных к окружности из одной точки:

отрезки касательных, проведенные из одной точки, равны и

составляют равные углы с отрезком, соединяющим эту точку с

центром окружности.

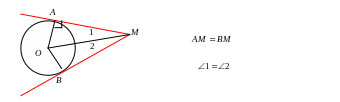
3). Свойство касательной и хорды, проведенных из одной точки:

угол между касательной и хордой равен половине дуги,

заключенной между ними.

5. Опорные задачи.

1). Свойство дуг, заключенные между параллельными хордами:

дуги, заключенные между параллельными хордами равны.

Если AB║CD, то AC =

2). Свойства равных центральных углов:

если равны центральные углы, то равны дуги, на которые они

опираются, и хорды, которые стягивают эти

дуги.

Если , то и

3). Свойства пересекающихся хорд : произведение отрезков хорд

равны.

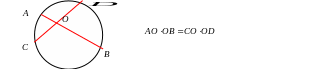
4). Свойство диаметра и хорды: диаметр окружности,

перпендикулярный к хорде, делит эту хорду пополам,

Если , то AH = HB

5). Свойство перпендикуляра, проведенного к диаметру:

перпендикуляр, проведенный из любой точки окружности к

диаметру, есть среднее пропорциональное между отрезками,

на которые перпендикуляр делит диаметр.

Если , то

6). Свойство секущих, проведенных из одной точки к окружности:

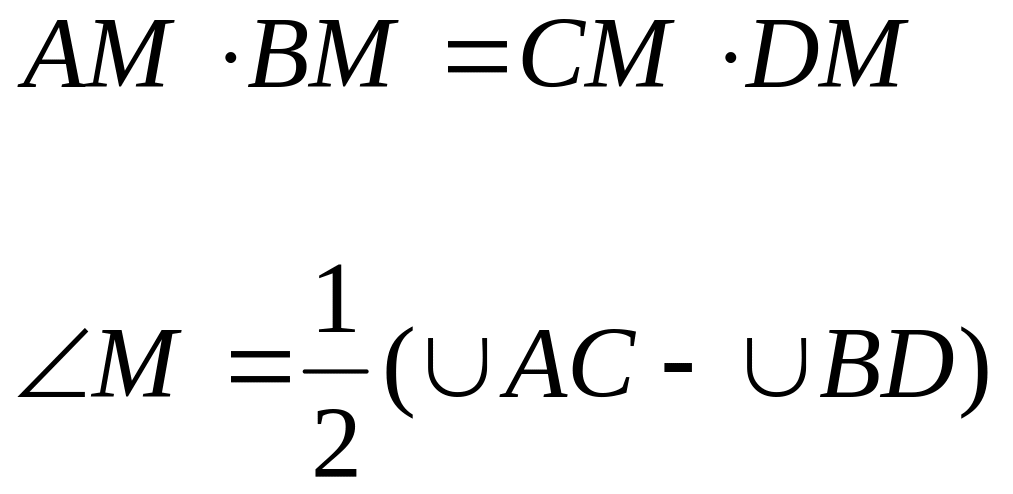
7). Свойство секущей и касательной, проведенных из одной точки

к окружности

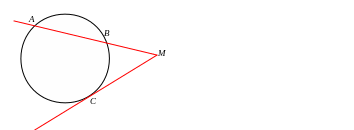
8). Площади сегментов:

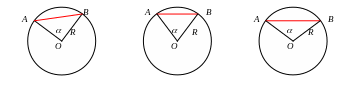
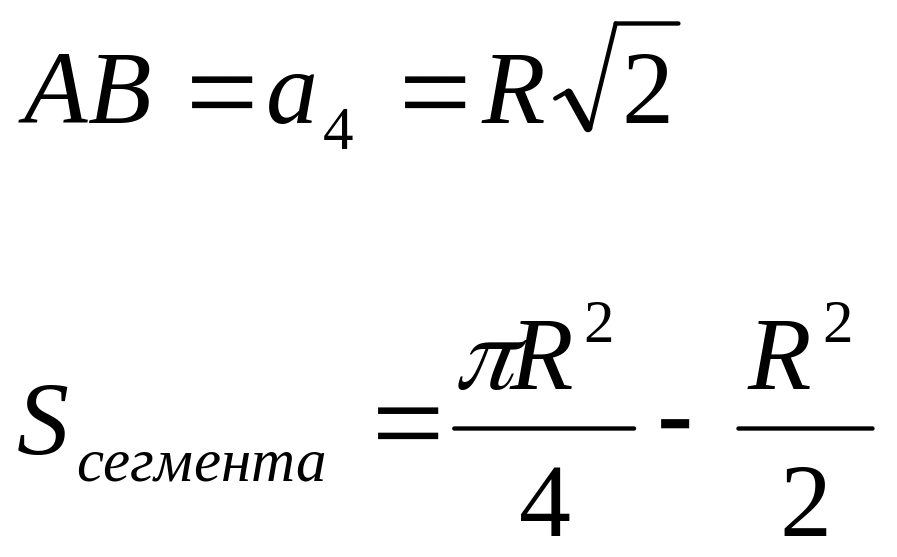
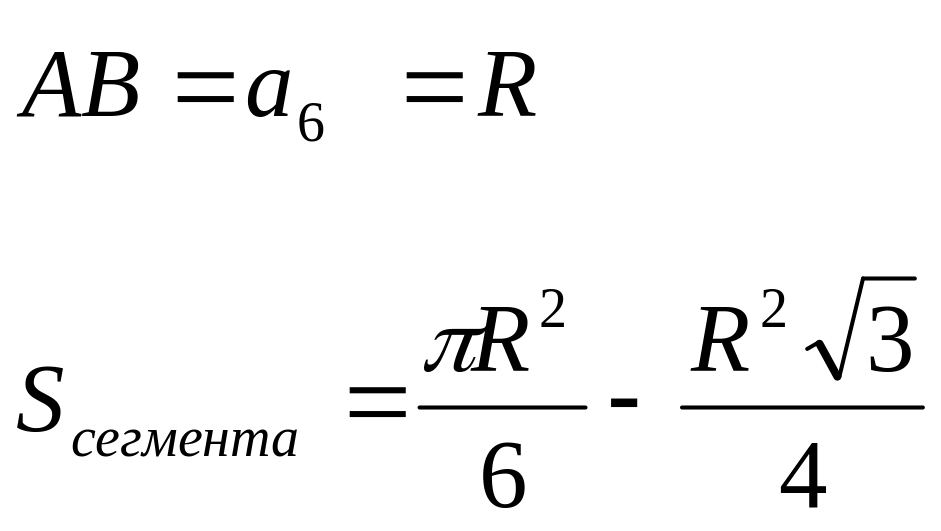
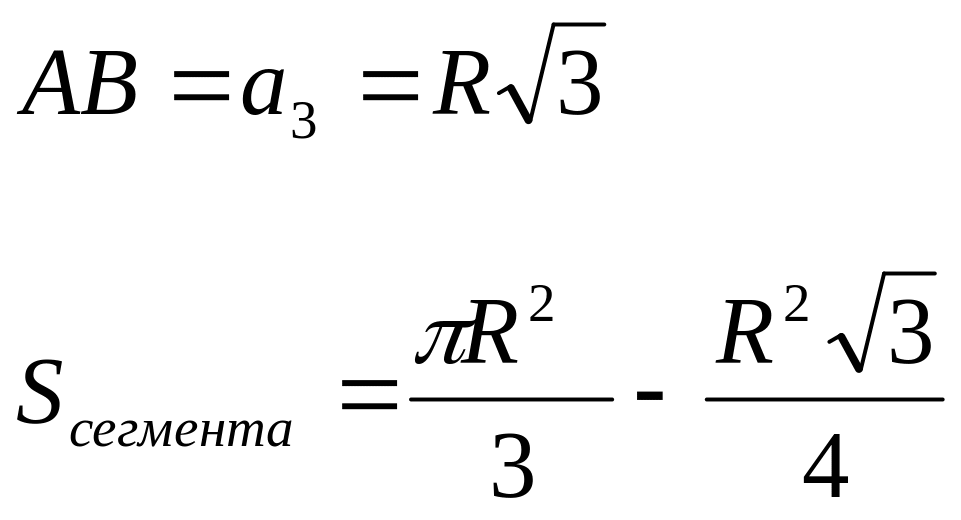
9). Связь длины хорды и расстояния ее от центра окружности:

хорда большей длины расположена ближе к центру.

Если AB > CD, то ОН < ОК