5. Опорные задачи.

1). Свойство ромба с углом 60°:

если в ромбе один из углов равен 60°, то у него меньшая диагональ равна стороне.

Если , то АB = AC.

2). Дополнительные свойства диагоналей параллелограмма:

а). сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех его сторон

б). при проведении диагоналей в параллелограмме площади полученных треугольников равны

B C

O

A D

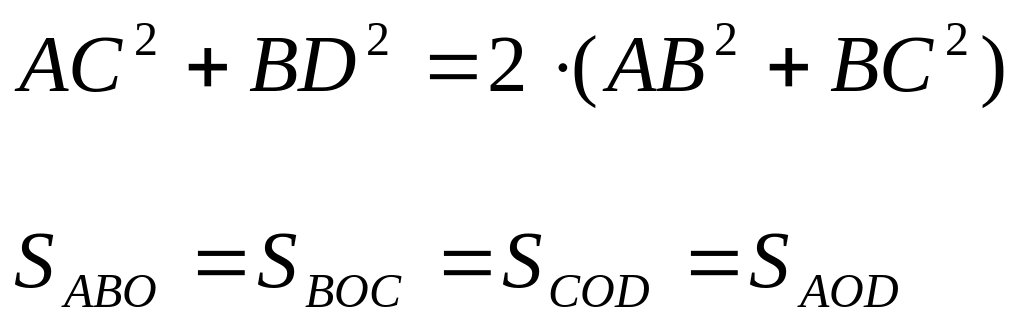
3). Свойство углов в четырехугольнике: сумма углов в четырехугольнике равна 360°.

4). Свойства биссектрис в параллелограмме:

а). биссектриса параллелограмма ( прямоугольника или трапеции) отсекает равнобедренный треугольник.

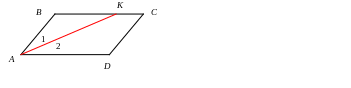
Если , то AB = BK

б). в параллелограмме биссектрисы смежных углов перпендикулярны,

в трапеции биссектрисы углов, прилежащих к боковым сторонам перпендикулярны

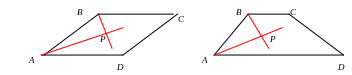
Если AP и DP –биссектрисы углов, то

5). Свойства треугольников, образованных при пересечении диагоналей в трапеции:

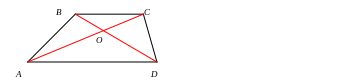
a). Δ AOD Δ BOC

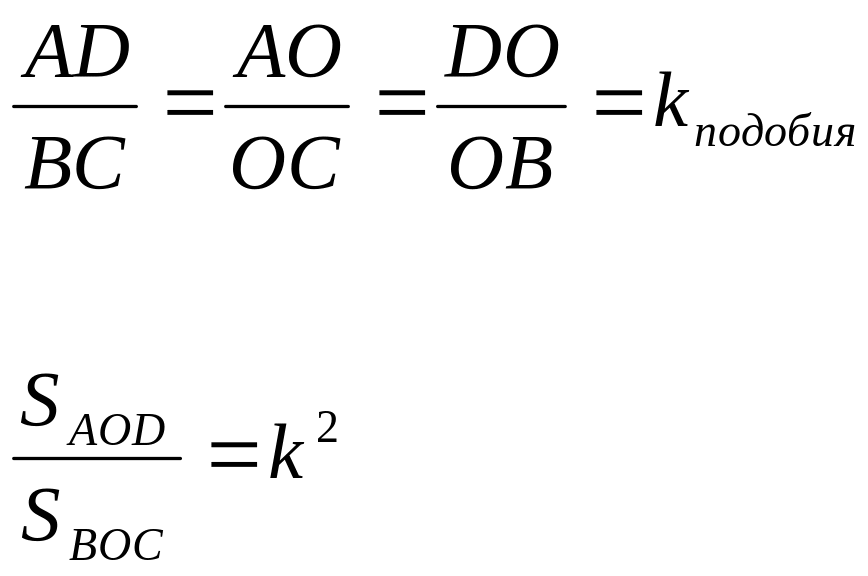
б). и

6). Свойство отрезка, соединяющего середины диагоналей трапеции:

середины диагоналей трапеции лежат на средней линии, а отрезок, соединяющий эти точки равен полу разности основании.

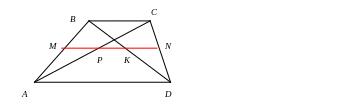
Если P и K – середины диагоналей, то

7). Свойство равнобедренной трапеции:

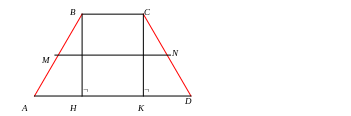
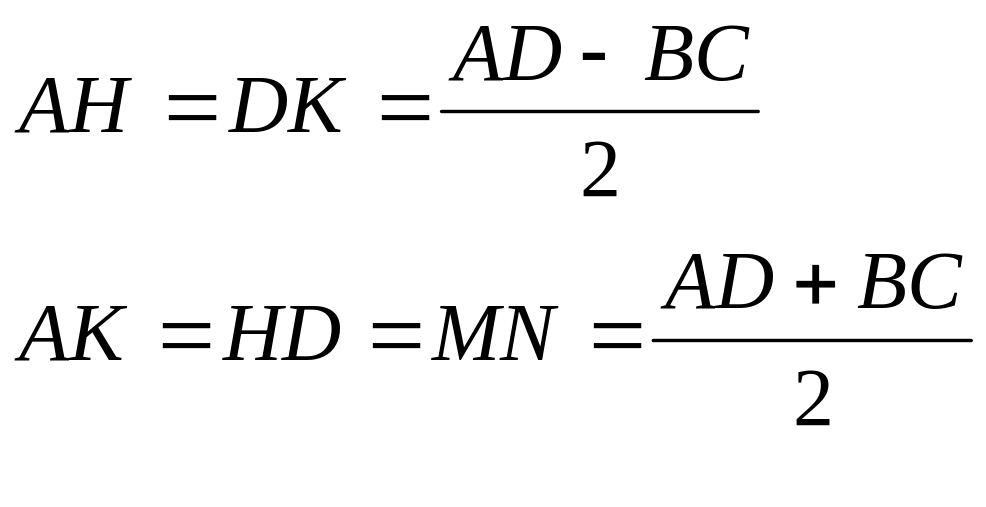
8). Свойство равнобедренной трапеции со взаимно перпендикулярными диагоналями: в равнобедренной трапеции с перпендикулярными диагоналями высота равна средней линии.

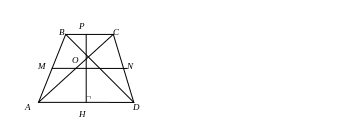
Если AB = CD и BD AC, то MN = PH и

9). Нахождение диагоналей в четырехугольниках:

квадрат прямоугольник ромб

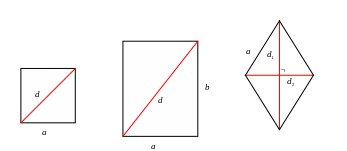
Окружность

1. Центральные и вписанные углы.

1. Свойства центральных и вписанных углов:

центральный угол равен дуге, на которую он опирается,

вписанный угол равен половине дуги, на которую он опирается.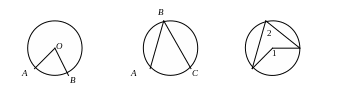

2. Свойство углов, опирающихся на одну дугу:

углы, опирающиеся на одну дугу равны.

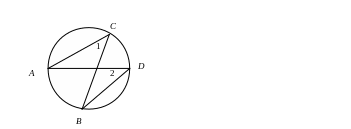
3. свойство вписанного угла, опирающегося на диаметр:

угол, опирающийся на диаметр – прямой.

Если АВ – диаметр, то