
. Множества.
Под множеством понимается совокупность объектов, объединенных по какому-нибудь признаку.
Объекты, из которых состоит множество называются элементами. Множество обозначается заглавными буквами латинского алфавита, а их элементы – малыми буквами (A, B, C; a, b, c)
![]() - элемент х
принадлежит множеству Х
- элемент х
принадлежит множеству Х
![]() - элемент х не
принадлежит множеству Х.
- элемент х не
принадлежит множеству Х.
Множества, не содержащие ни одного элемента называются пустыми Ø
Множество А
называется подмножеством множества В,
если каждый элемент множества А
![]() множеству В.
множеству В.
А
![]() В (А входит в В) или (
В (А входит в В) или (![]() ).
).
Множества А и В равны или совпадают, если А В и В А; А = В.
Объединением множеств А и В называется множество состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств
![]()
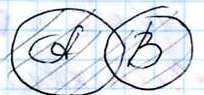
Это можно показать на диаграммах Венна:
П ересечением
множеств А и В называется множество,
состоящее из элементов, каждый из которых
принадлежит и множеству элементов А и
множеству В.
ересечением
множеств А и В называется множество,
состоящее из элементов, каждый из которых
принадлежит и множеству элементов А и
множеству В.
![]()
Некоторые логические символы:
1.
![]() (из предложения
(из предложения
![]() следует предложение
следует предложение
![]() )
)
2.
![]() (предложение
и
равносильны;
верно тогда и только тогда, когда верно
)
(предложение
и
равносильны;
верно тогда и только тогда, когда верно
)
3.
![]() (знак существования)
(знак существования)
4.
![]() (для любого, для каждого)
(для любого, для каждого)
5. : (такое что, имеет место)
6.
![]() (знак соответствия)
(знак соответствия)
Основные числовые множества.
![]() - множество
натуральных чисел.
- множество
натуральных чисел.
![]() - целые числа.
- целые числа.
![]() - множество
рациональных чисел.
- множество
рациональных чисел.
R ….. – множество действительных чисел, эти числа выражаются десятичными дробями, или бесконечными дробями.
U – множество иррациональных чисел.
![]()
можно составить цепочку
![]()
• Числовыми промежутками (интервалами) называются подмножества всех действительных чисел, имеющих следующий вид.
путь
![]() ,
,
![]() <
<
![]() , тогда а – это левый, b
– это правый концы промежутка.
, тогда а – это левый, b
– это правый концы промежутка.
![]() - называется
отрезком или замкнутым интервалом.
- называется
отрезком или замкнутым интервалом.
![]() - открытый промежуток.
- открытый промежуток.
![]() - полуоткрытый
интервал.
- полуоткрытый
интервал.
![]() - полуоткрытый
промежуток.
- полуоткрытый
промежуток.
![]() - полубесконечный
интервал.
- полубесконечный
интервал.
![]() - полубесконечный
интервал.
- полубесконечный
интервал.
![]() - полубесконечные
интервалы, с одной стороны замкнуты.
- полубесконечные
интервалы, с одной стороны замкнуты.
![]() - бесконечный
интервал.
- бесконечный
интервал.
• Определение.
Пусть точка
![]() ,
окрестностью этой точки называется
любой интервал от (а, b)
содержащий т.
,
окрестностью этой точки называется
любой интервал от (а, b)
содержащий т.
![]() .
Для (любого
.
Для (любого![]() )
)
![]()
![]() 0 окрестность (
0 окрестность (![]() )
называется
- окрестностью
точки
,
где
называется центром окрестности, а
- радиусом окружности.
)
называется
- окрестностью
точки
,
где
называется центром окрестности, а
- радиусом окружности.

Для любого х
принадлежащего этой окрестности,
выполняется неравенство
![]() <
.
<
.
или
-
<
![]() <
<
-
+
<
![]() <
+
<
+
Определение функции. Способы задания.
Определение.Даны
два не пустых множеств х и у, соответствие
f
которых каждому элементу множества
сопоставляет один и только один элемент
множества
![]() называется функцией
и записывается
называется функцией
и записывается
![]()
![]()
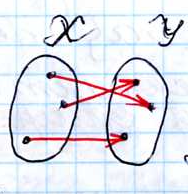
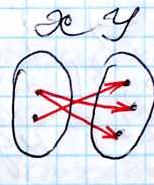

не является функцией, является функцией не является функцией, т. к.
т. к. не для каждого x одному х соответствует
существует свой у. несколько у
Множество х называется областью определения функции. Обозначается Д (f)
Множество У называется множеством значений функций, обозначается Е (f).
Если элементы множества Х и У действительно числа, то функция f называется числовой. Элемент х называется аргументом (не зависимой переменной), элемент у – функцией (зависимой от х переменной). В этом случае говорят, что х и у находятся в функциональной зависимости.
• Определение. Графиком функции y = f(x) называется множество всех точек плоскости по Оху, для каждой из которых х – значение аргумента, а у – соответствующее ему значение функции.
Основные способы задания функции:
1. аналитический - функция задается в виде нескольких формул или уравнений.
2. табличный, т. е. функция задается таблицей ряда значений аргумента и соответствующих этим значениям значений функций.
3. графический- функция задается графиком функций.
• График функций можно построить с помощью преобразований графиков известных функций.
Пусть известен график функции y = f(x).
1) гр. ф.
![]()
получается из
графика функции f(x)
сдвигом вдоль оси у на
![]() единиц (если а > 0, то вверх, если а <
0, то вниз).
единиц (если а > 0, то вверх, если а <
0, то вниз).
2)
![]() получается из графика функций f(x)
сдвигом вдоль оси х на
получается из графика функций f(x)
сдвигом вдоль оси х на
![]() единиц (если
<
0, то вправо, если
> 0, то влево).
единиц (если
<
0, то вправо, если
> 0, то влево).
3) график функции
![]() получается из графика функции f(x)
растяжением вдоль оси у в k
раз.
получается из графика функции f(x)
растяжением вдоль оси у в k
раз.
4) график функции
![]() получается из графика функции f(x)
сжатием в m
раз вдоль оси Ох.
получается из графика функции f(x)
сжатием в m
раз вдоль оси Ох.
5) график функции
![]() получается из графика функции f(x)
симметричным отображением относительно
оси Ох.
получается из графика функции f(x)
симметричным отображением относительно
оси Ох.
6)
![]() получается из графика функции f(x)
симметричным отображением относительно
оси Оу.
получается из графика функции f(x)
симметричным отображением относительно
оси Оу.
