7.4.1 Расчет рабочей арматуры пристенного ребра
Для сечения с одиночным армированием проверяем условие, определяющее положение нейтральной оси. Предполагаем, что нейтральная ось проходит по нижней грани полки, и определяем область деформирования для прямоугольного сечения шириной .
;
d = h
– c = 200 – 25 = 175
мм;
,
что указывает на то, что сечение
находится в области деформирования 2.
По формуле таблице 6.6 [14] находим величину изгибающего момента, воспринимаемого бетоном, расположенным в пределах полки:
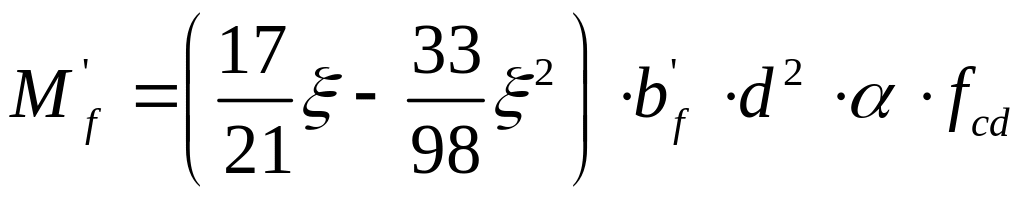(7.22)
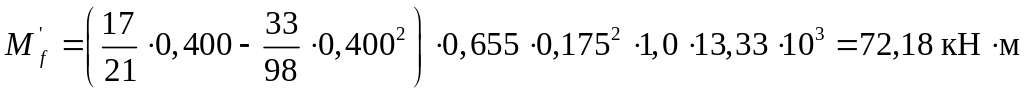
Поскольку выполняется условие , нейтральная ось располагается в пределах полки, в связи с этим дальнейший расчет производим как для прямоугольного сечения, имеющего размеры = 655 мм, d = 175 мм.
Определяем коэффициент
по формуле 7.3
;
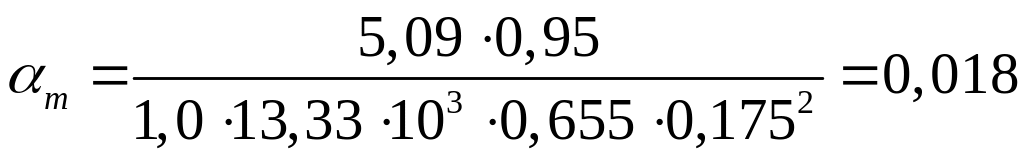По таблице 6.7 [14] при = 0,018 определяем, что сечение находится в области деформирования 1а, отсюда η = 0,979.
Находим величину требуемой площади растянутой арматуры по формуле 7.7
.
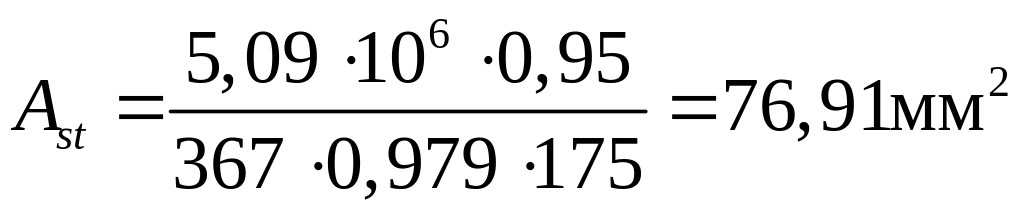По таблице сортамента арматуры принимаем
один стержень диаметром 10 класса S400,
для которого
=
78,5
>
,
где
определено по таблице
11.1[4]:
> 0,13. Принимаем
=0,143.
7.4.2 Расчет прочности пристенного ребра на действие поперечной силы
Поперечная сила от полной расчетной
нагрузки
5,90 кН, с учетом коэффициента
0,95:
5,90·0,95 = 5,61 кН.
Расчет производим на основе расчетной модели наклонных сечений.
Проверяем прочность пристенного ребра по наклонной полосе между наклонными трещинами в соответствии с условием (7.12).
Определяем
по формуле (7.13):
– по формуле (7.14),
– по формуле (7.15),
где
28,3
– площадь сечения одного поперечного
стержня Ø6мм класса S240.
S
,
принимаем на опорном участке шаг стержней
равный 100
,
на остальном участке пролёта
.
;
определено по пункту 11.2.5 [4];
<1,3
– коэффициент, определяемый по формуле
(7.16)
;
;
Следовательно, прочность по наклонной полосе между наклонными трещинами обеспечена.
По формуле (7.17) определяем поперечную силу, воспринимаемую бетоном и поперечной арматурой.
, (7.17)
где – коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах и определяемый по формуле (7.18)
При этом
=
655 мм;
= 115 мм;
=
655 – 115 = 540 мм > 3·
=
3·70 = 210 мм.
Для расчета принимаем = 210 мм.
,
принимаем
;
– усилие в поперечных стержнях на единицу длины элемента, определяемое по формуле (7.19),
где = 174 МПа – расчетное сопротивление поперечной арматуры (табл. 6.5 [5]).
;
;
.
Следовательно, прочность на действие поперечной силы по наклонной трещине обеспечена.
Поперечные ребра армируем конструктивно с помощью каркасов Кр-3 с рабочей арматурой, требуемая минимальная площадь поперечного сечения которой равна:
где
=67,5мм.
=
h – c=200-(20+10/2)=175мм.
Принимаем диаметр рабочей арматуры
равным 10мм класса S400, для
которого
=78,5
мм2, с поперечной арматурой
диаметром 6мм класса S240
и монтажной арматурой диаметром 10 мм
класса S240.
.