Вопрос 15. Моделирование и идентификация динамических систем.

Понятие "динамическая система" шире, чем понятие "промышленный объект". Известно что, динамические модели объектов управления являются более сложными, они отражают влияние на объект временных характеристик не только в данный момент, но и в прошлые моменты времени.

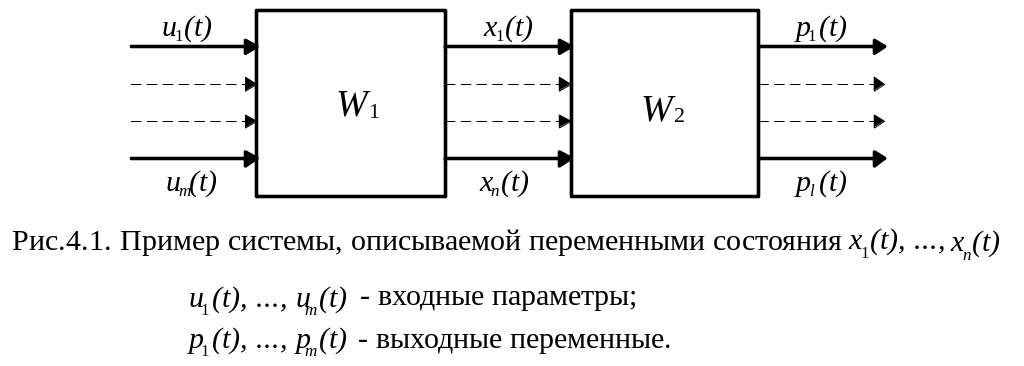
Состояние динамической системы описывается совокупностью физических переменных состояния x₁(t) ,…, x_n(t), характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.

При этом переменные состояния x₁(t), x₂(t)…, x_n(t) позволяют по начальным значениям переменных x₁(t₀), x₂(t₀)…, x_n(t₀), т.е. в начальный момент времени t₀, и заданным воздействиям u₁(t) ,…, u_m(t) при t ³ t₀ определить будущие значения переменных состояния и выходных переменных (рис.4.1).

Корректная постановка математической задачи синтеза оптимального управления динамическими системами предполагает, что у разработчика системы имеется такая информация:

• переменные, описывающие параметры состояния системы и параметры управления;

• математическая модель процесса функционирования динамической системы объекта управления;

• одномерная или многомерная функция - критерий качества управления, с помощью которого выражается цель управления;

• математические соотношения, описывающие ограничения, налагаемые на переменные состояния или управления.

Обычно на практике рассматриваются системы, процесс функционирования которых протекает во времени. Кроме того, современный подход к математическому описанию динамических систем состоит в описании систем в пространстве состояний. Аргументом входных и выходных сигналов системы может служить время, пространственные координаты, а также некоторые специальные переменные.

Любая математическая модель динамической системы, в конечном счете, строится по результатам наблюдений за входными и выходными сигналами. Такую процедуру, принято называть идентификацией, в данном случае, идентификацией динамических объектов.

Активная идентификация предполагает, что исследователь выбирает рациональные моменты (или периоды) наблюдений за входами и выходами системы, задает определенные начальные условия или подает на вход специальный управляющий (тестирующий или пробный) сигнал и т.д. Следовательно, активная идентификация - это логическое развитие концепции активного эксперимента в статике.

Математическая модель в данном случае рассматривается как упрощенное отображение существенных сторон реальной системы, выраженное в математической форме.

При идентификации динамических систем под математической моделью понимают правило преобразова­ния входных сигналов Х в выходные сигналы Р. Преобразование входных сигналов в выходные, т. е. математическую модель си­стемы, можно представить в общем виде с помощью некоторого оператора системы А { }:

Р= А {Х }

Х Р

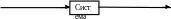
Вектор входных сигналов Вектор выходных сигналов

Рис. Принципиальная блок-схема системы

Под символом А { } понимаются любые математические действия (алгебраические операции, дифференцирование, интегрирование, решение алгебраических, дифференциальных, интегральных и лю­бых других функциональных уравнений, а также логические дей­ствия). Таким образом, оператор представляет собой совокуп­ность математических и логических операций, позволяющих установить соответствие между входными и выходными сигна­лами.

Существует большое разнообразие математических моделей производственных объектов. Их можно классифицировать по са­мым различным признакам. За основу классификации можно при­нять, в первую очередь, те или иные признаки (свойства) опера­тора A{ }.

Опера­тор системы преобразует векторную функцию Х(t) в векторную функцию Р(t). Такой оператор сам по себе может зависеть от вре­мени t:

A=A(t)=A

Модели подобного типа называют динамическими (вре­менными). Если свойства преобразования входных сигналов (функций), т. е. структура и свойства оператора А { }, не изменяются со временем, то динамическую систему (модель) называют стацио­нарной. В противном случае ее именуют нестационарной. Реакция стационарной системы на любой заданный тип возмущения за­висит только от интервала времени между моментом начала дей­ствия входного возмущения и данным моментом времени.

Если процесс развивается одновременно и во времени, и в про­странстве, например, по одной координате L, то оператор может преобразовывать входную векторную функцию z(t,L) в выходную векторную функцию (t, L), и сам по себе он тоже может зависеть от обоих этих аргументов:

A=A(t,L)=A _t,L

Эти модели называют пространственно-временными.

К простейшим динамическим моделям относят, например, регрессионную модель.

y = a₀ + a₁x₁(t) + a₂x₂(t) +….. + a_nx_n(t)

18