7 Завдання для самостійної роботи студентів

7.1 Завдання 1

Використовуючи метод Зейделя відшукати розв’язок рівняння з точністю :

1.1. ; .

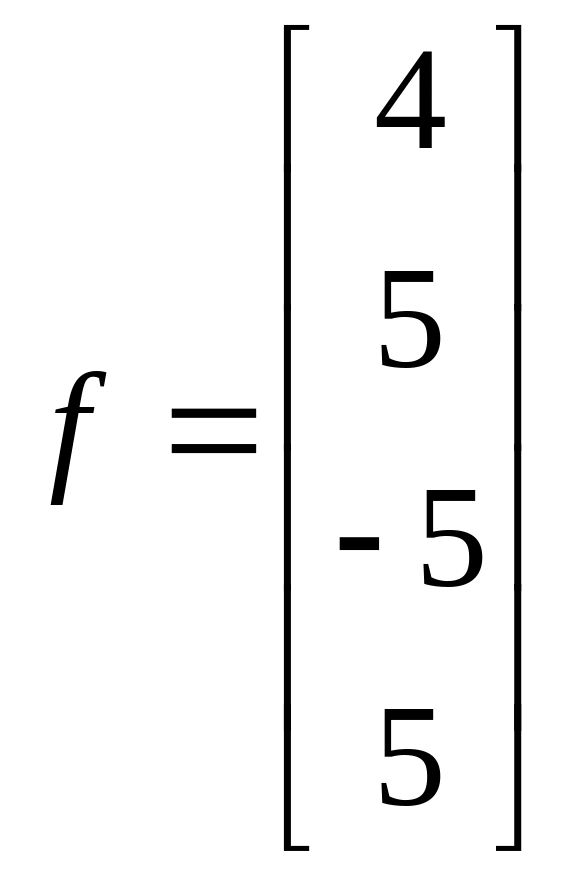1.2. ; .

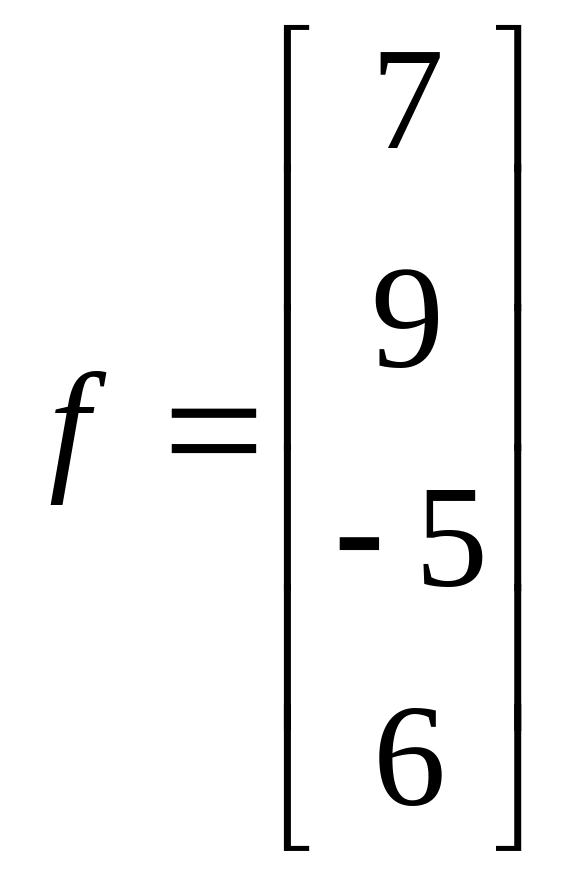1.3. ; .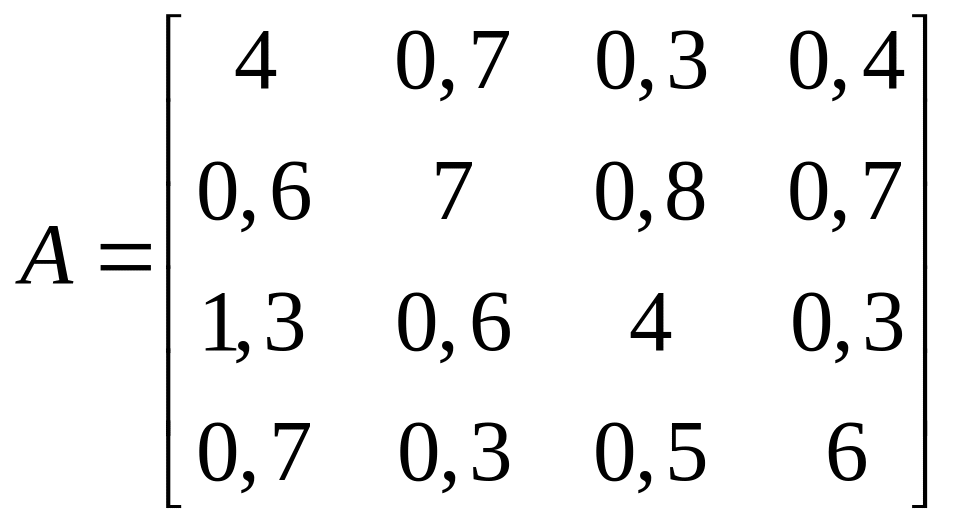

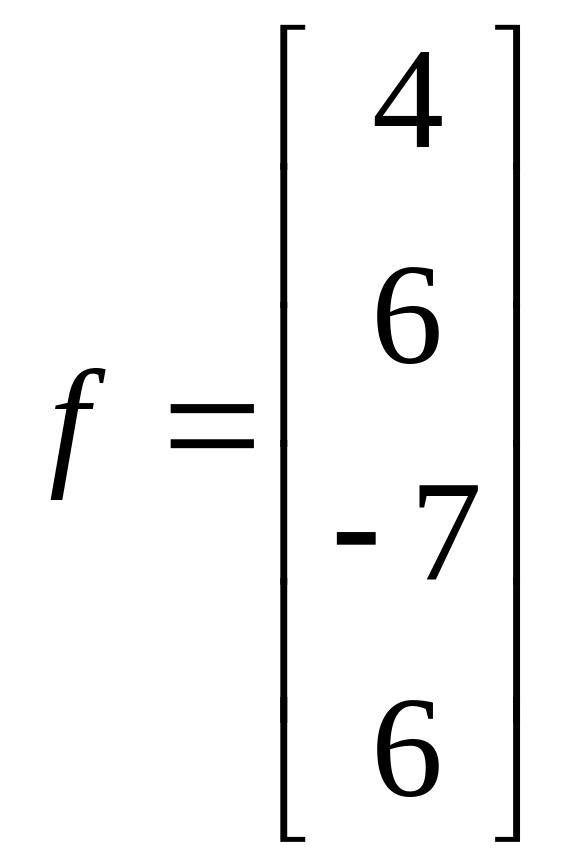1.4. ; .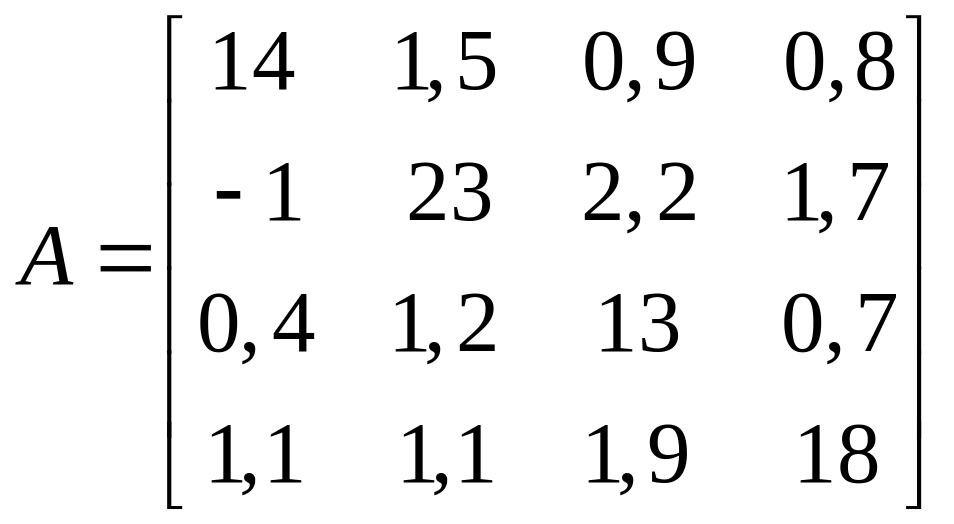

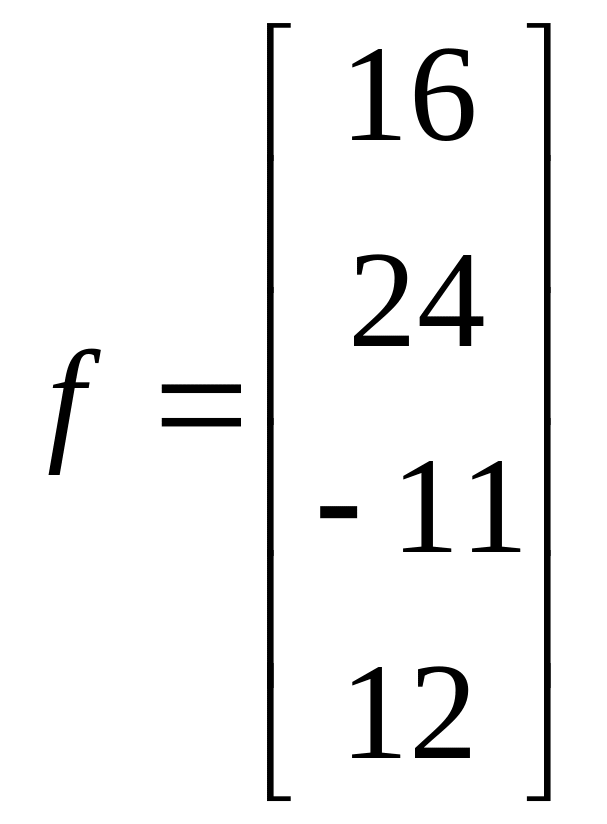1.5. ; .

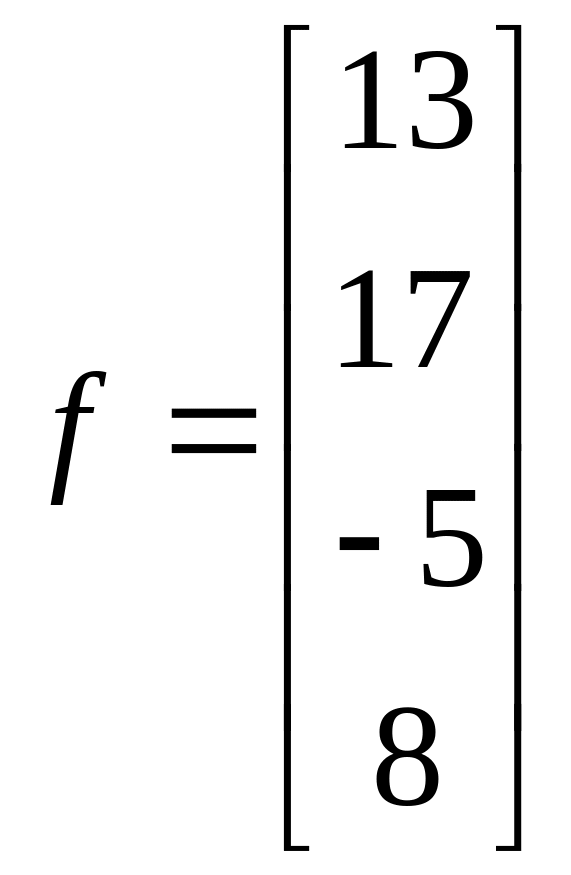1.6. ; .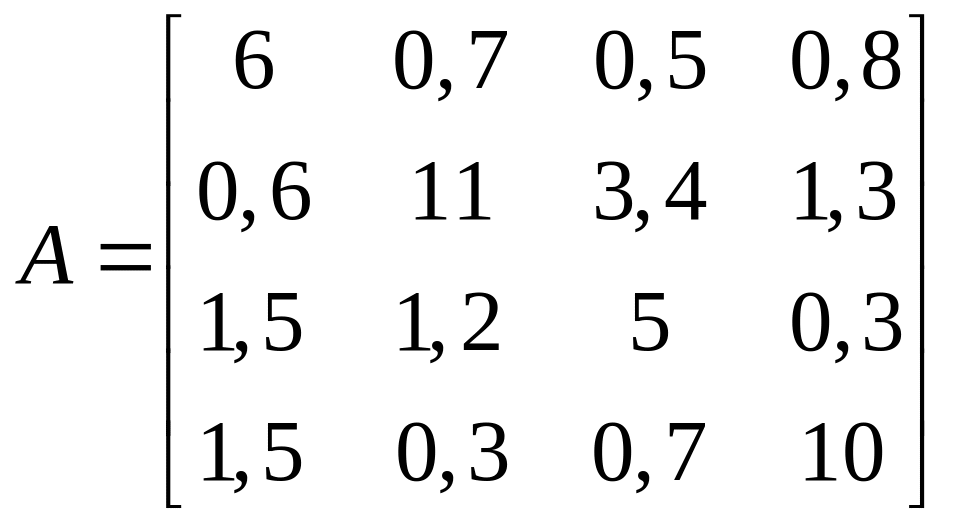

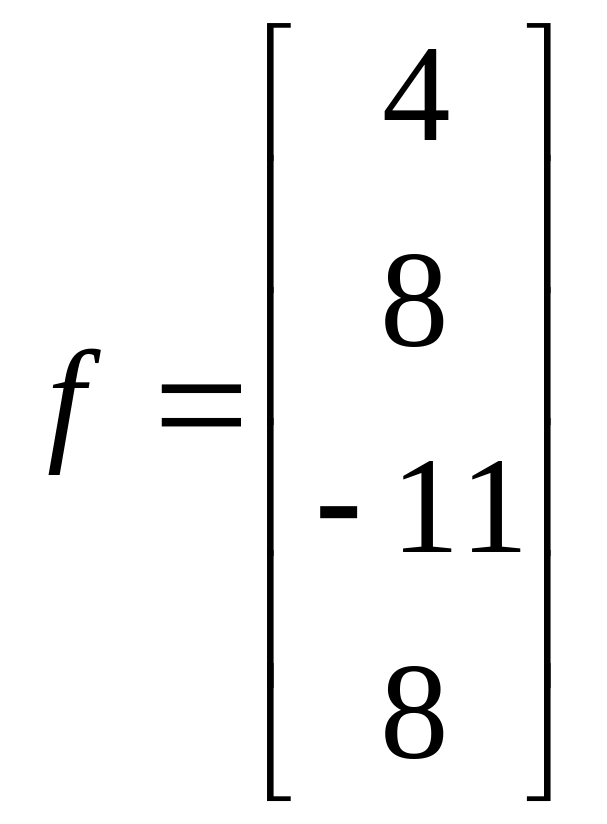1.7. ; .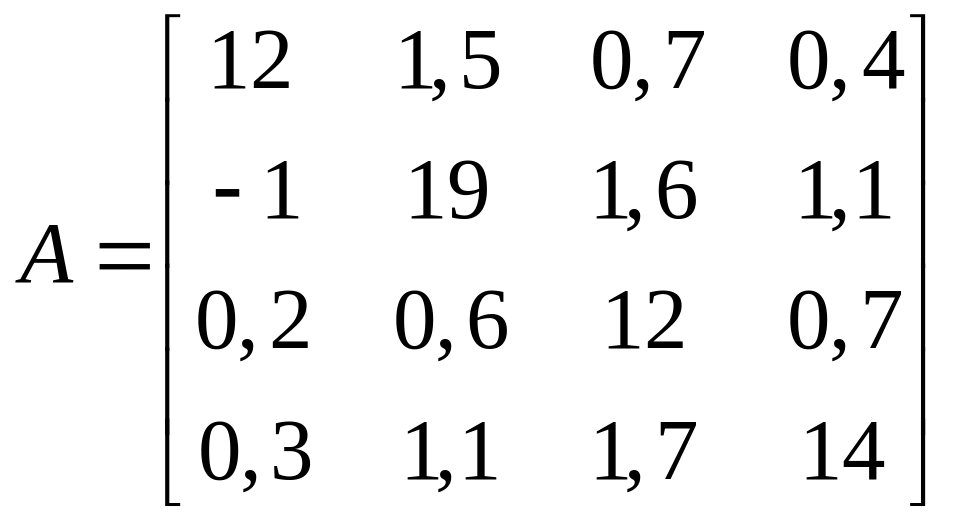

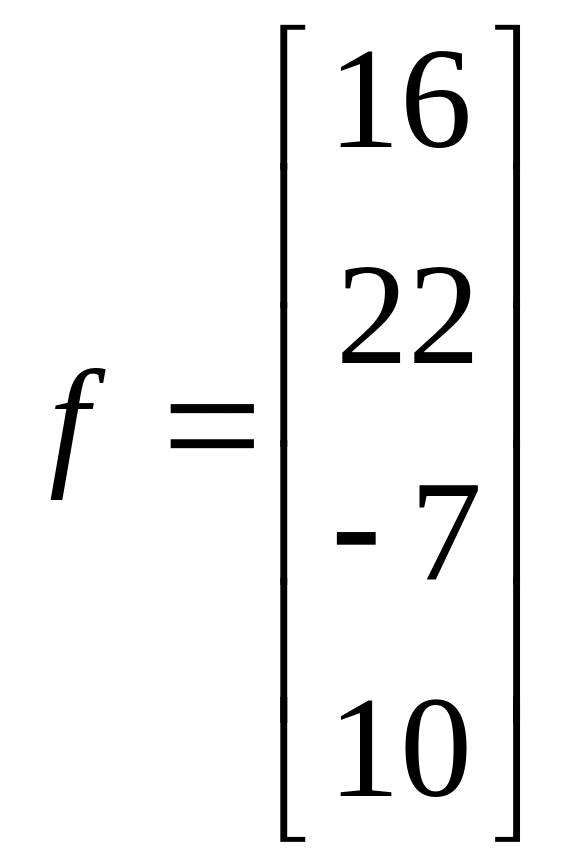1.8. ; .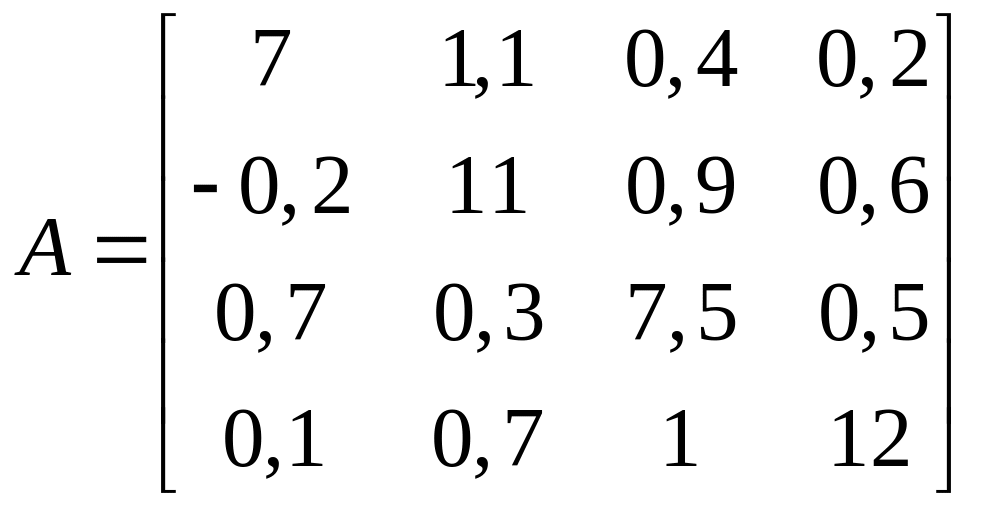

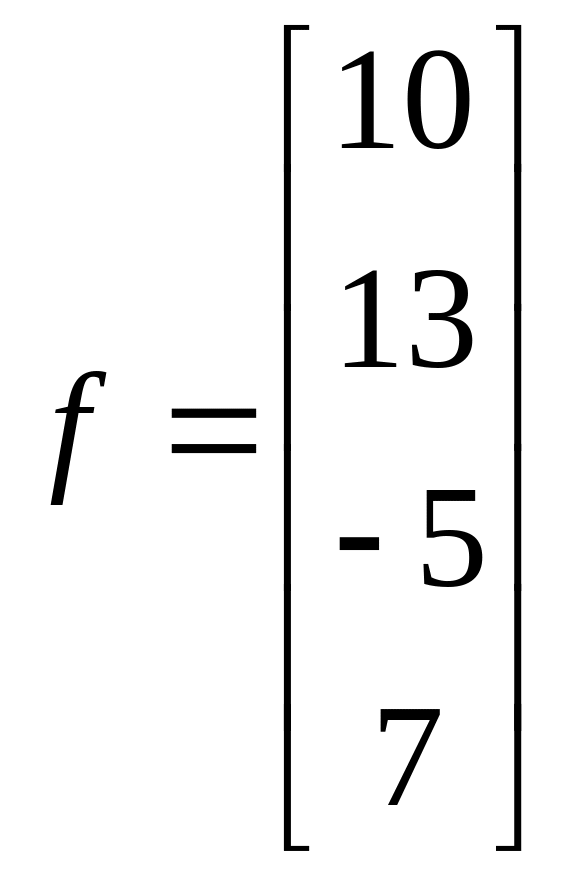1.9. ; .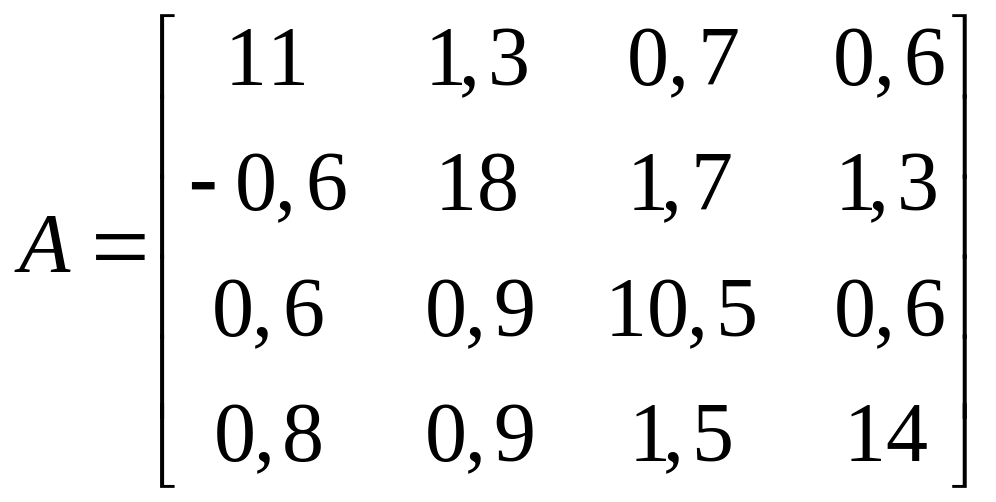

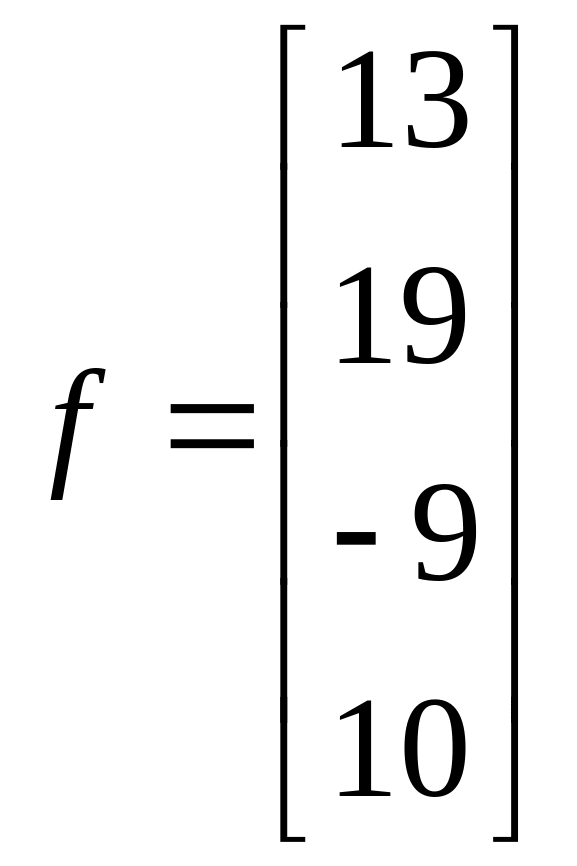1.10. ; .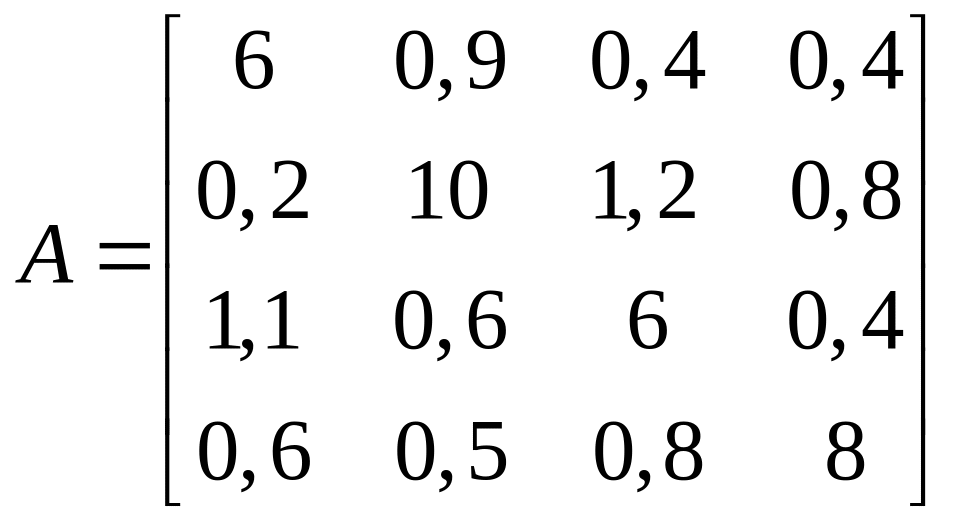

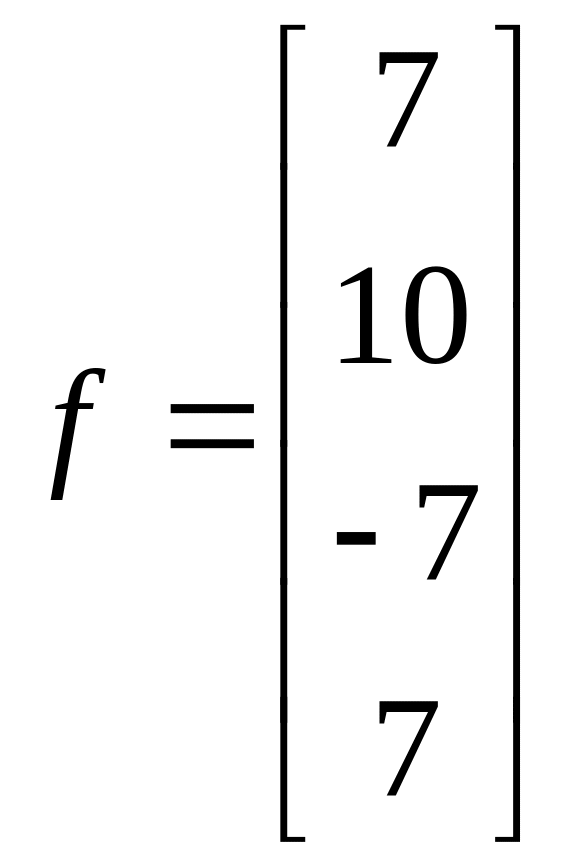1.11. ; .

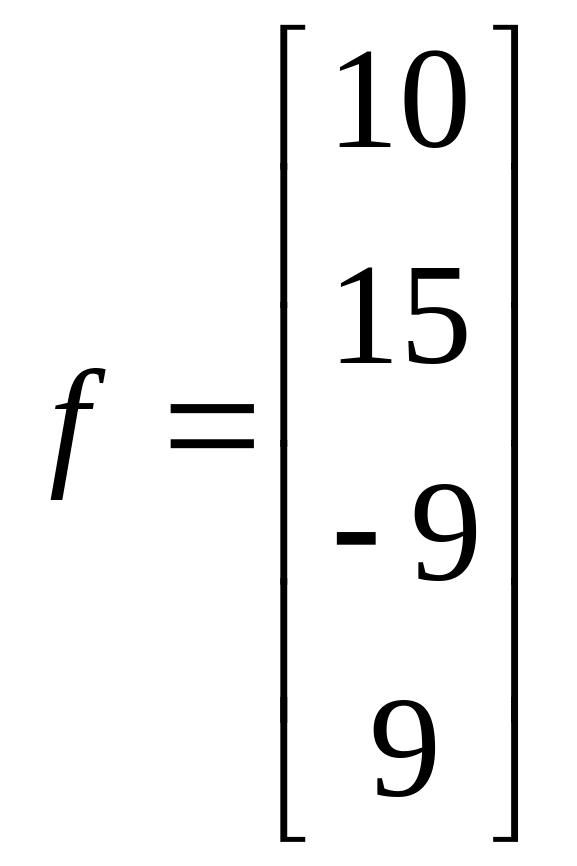1.12. ; .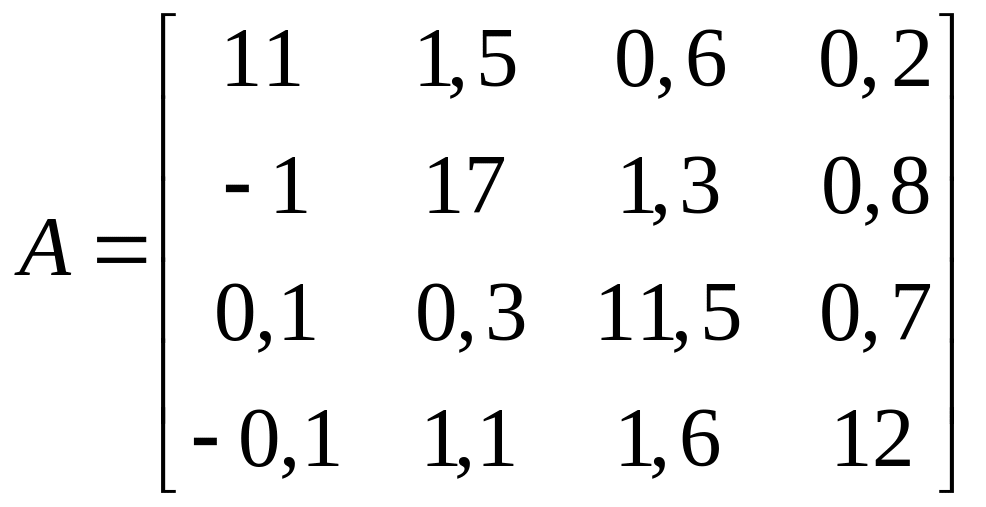

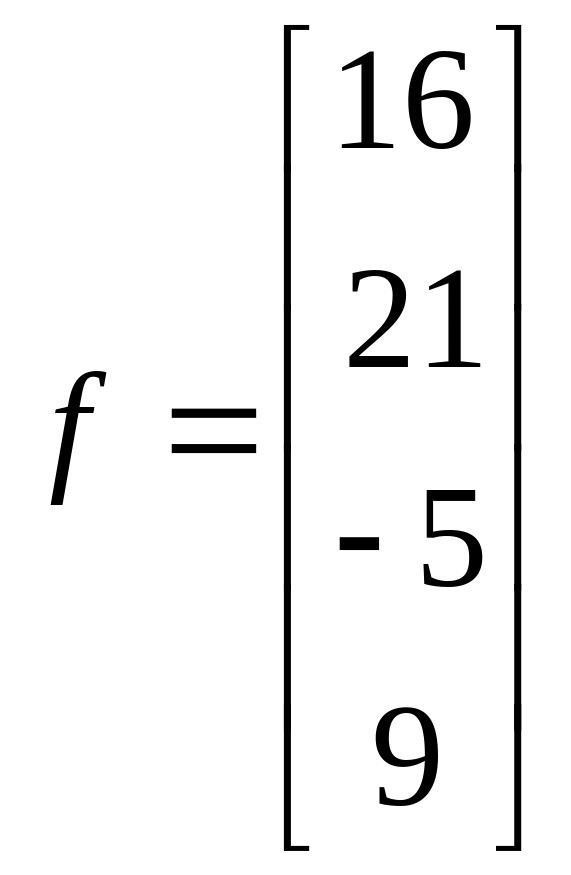1.13. ; .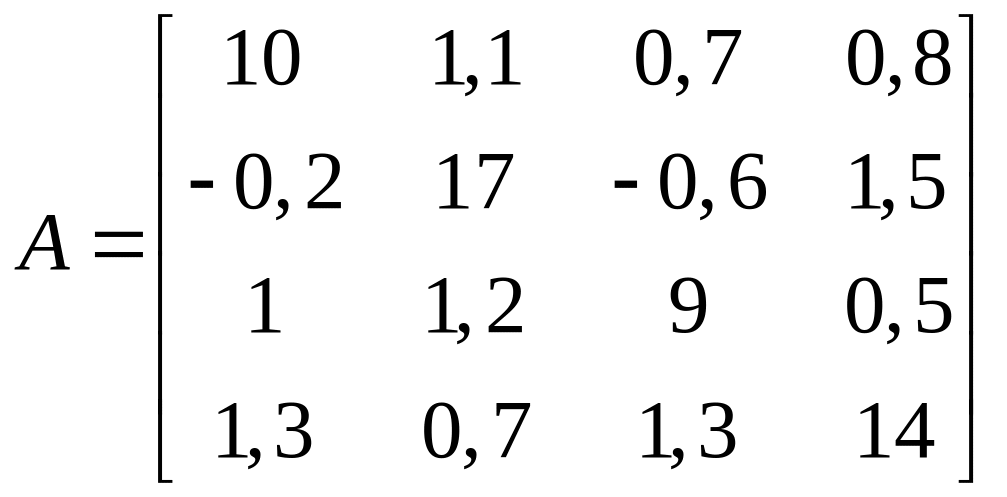

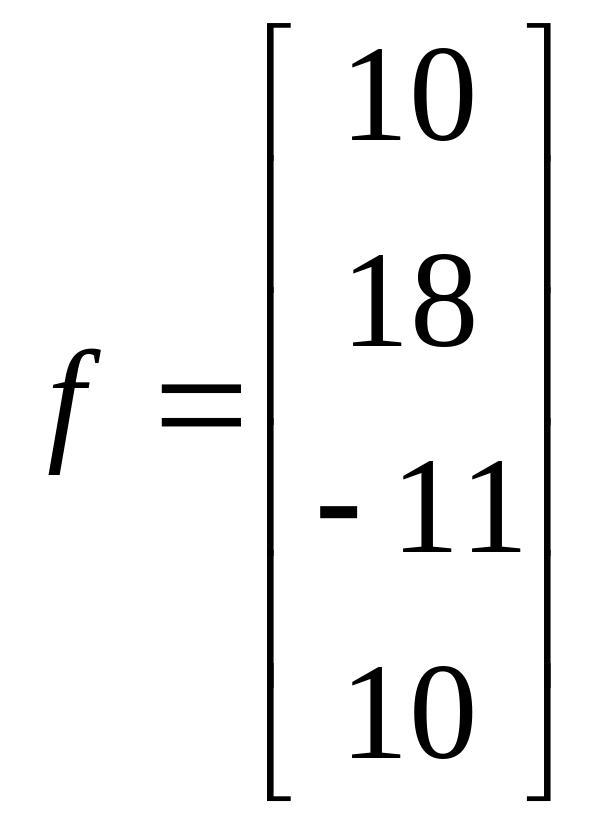1.14. ; .

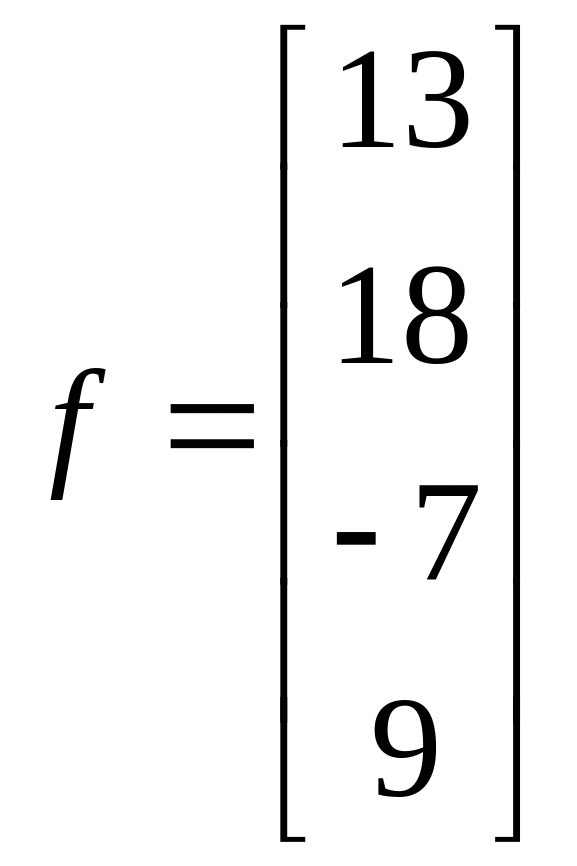1.15. ; .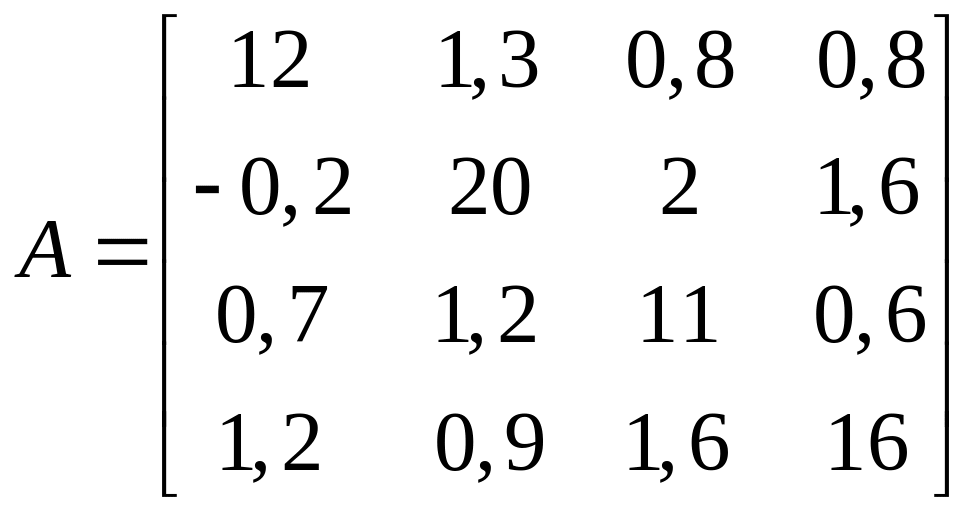

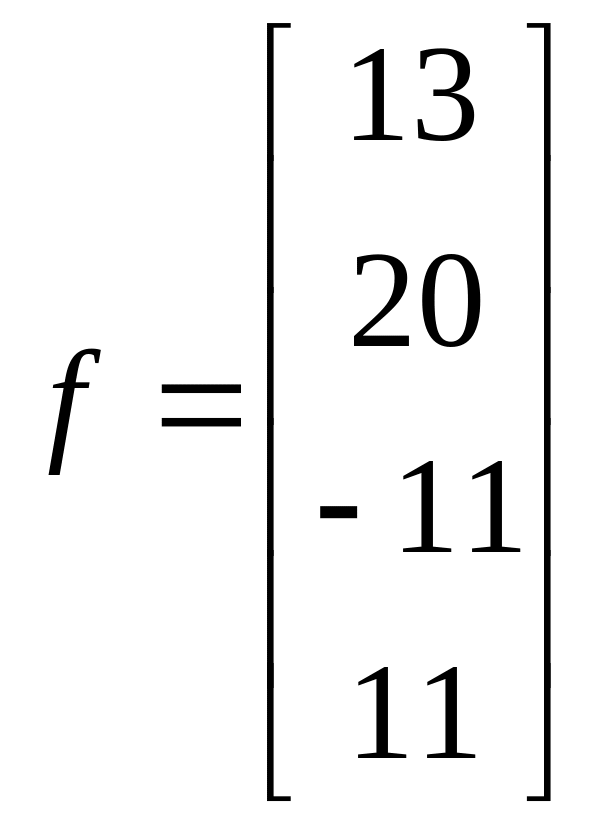1.16. ; .

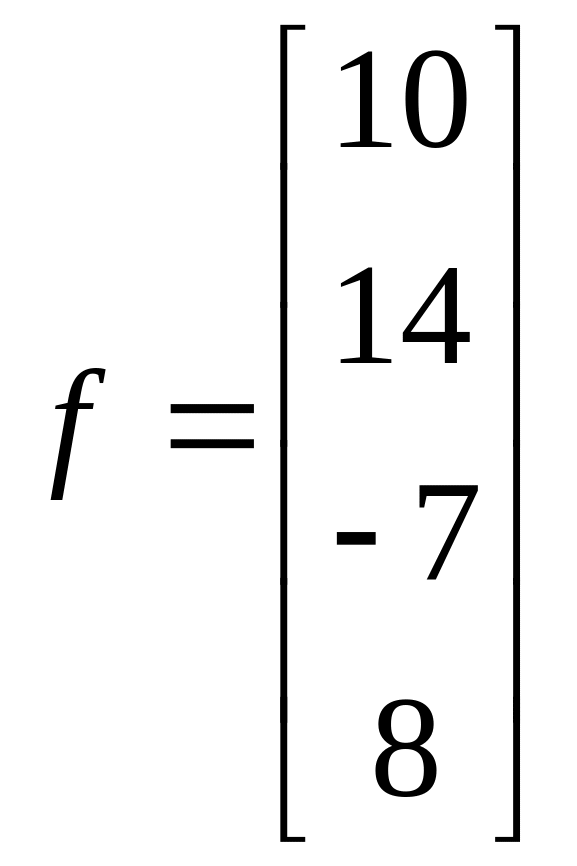1.17. ; .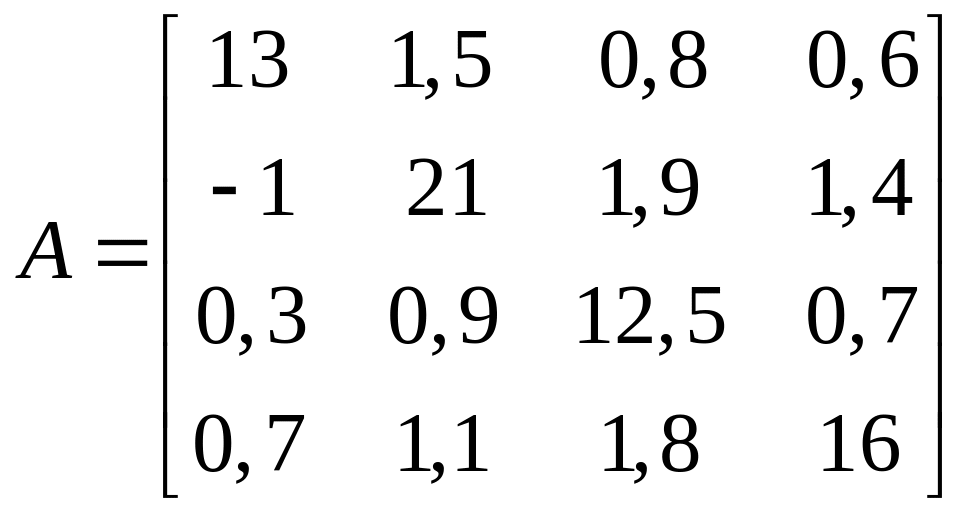

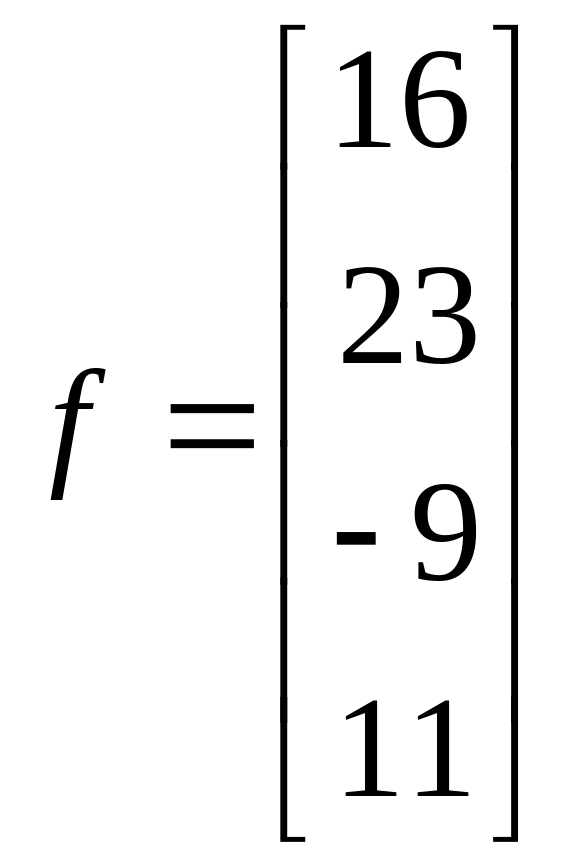1.18. ; .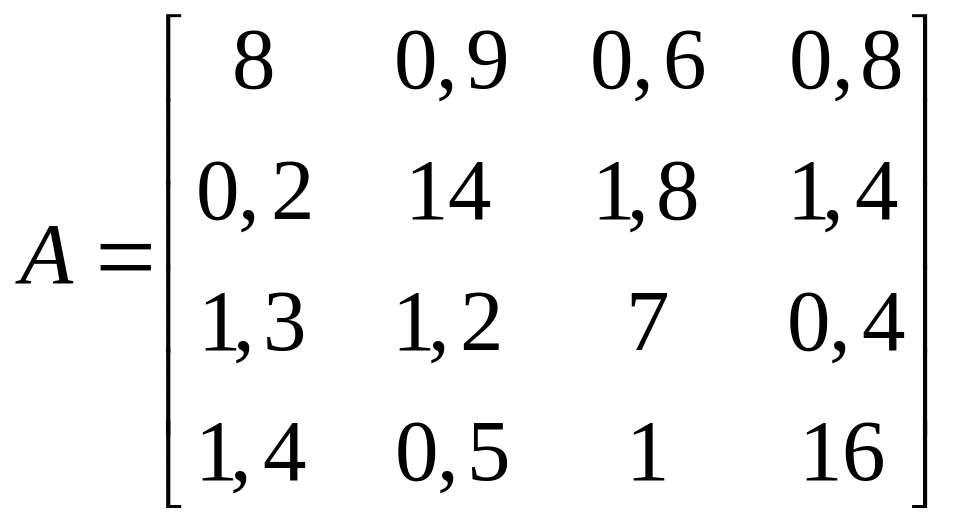

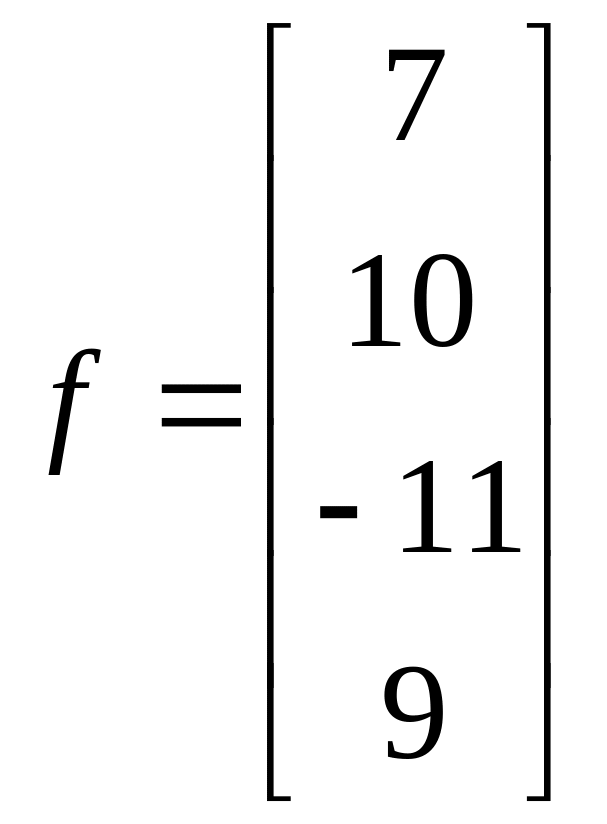1.19. ; .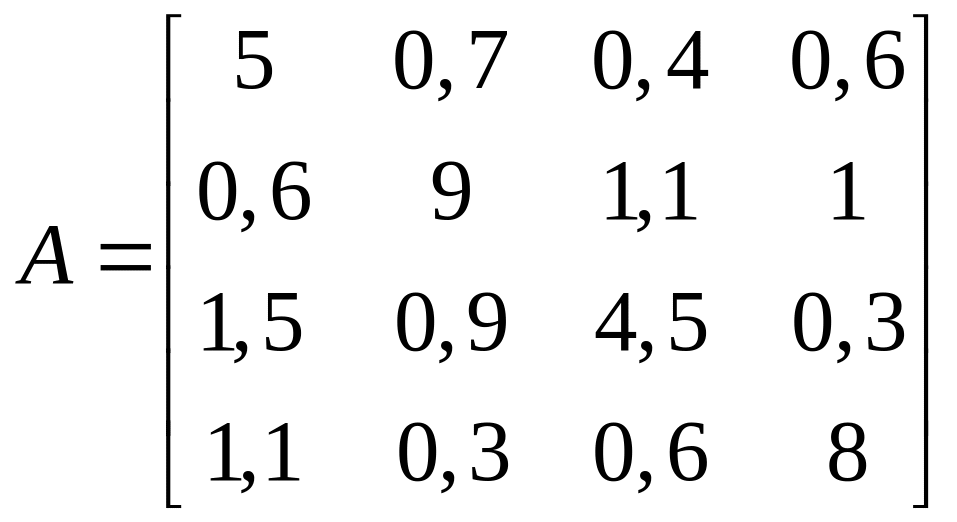

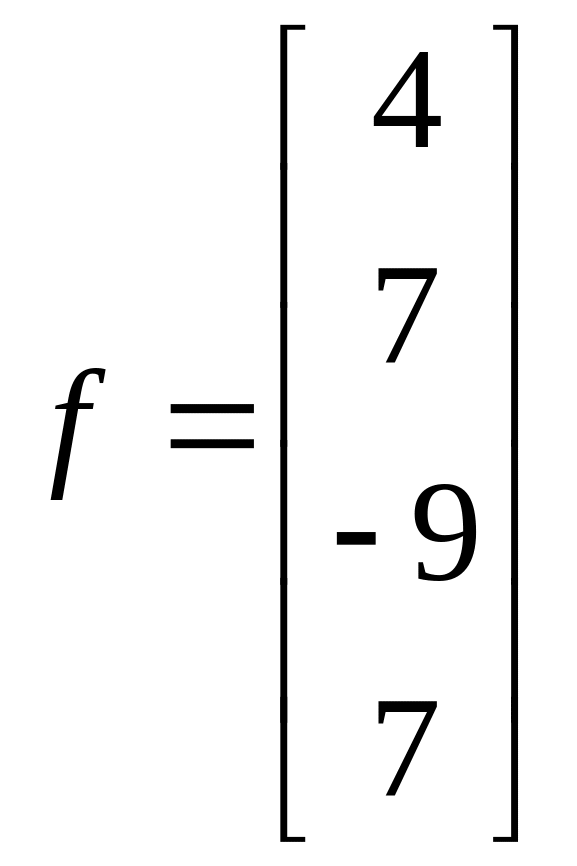1.20. ; .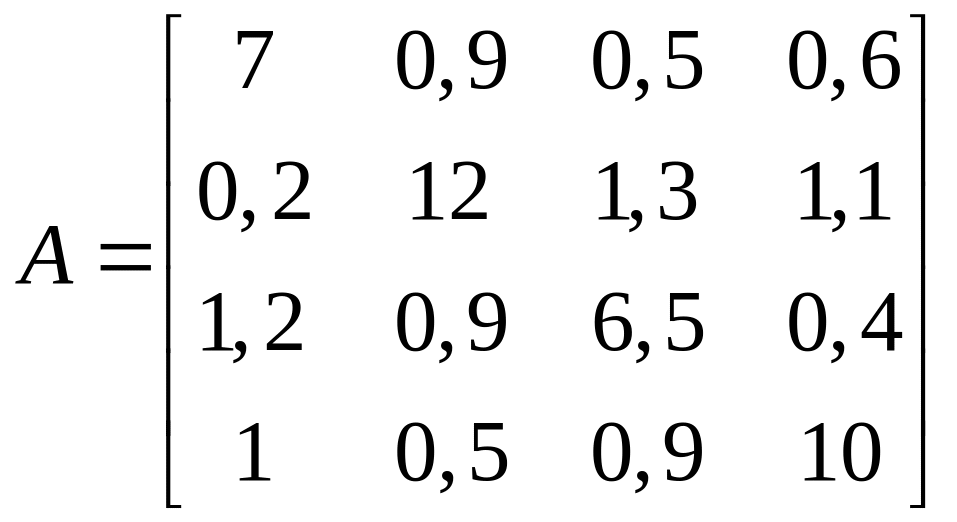

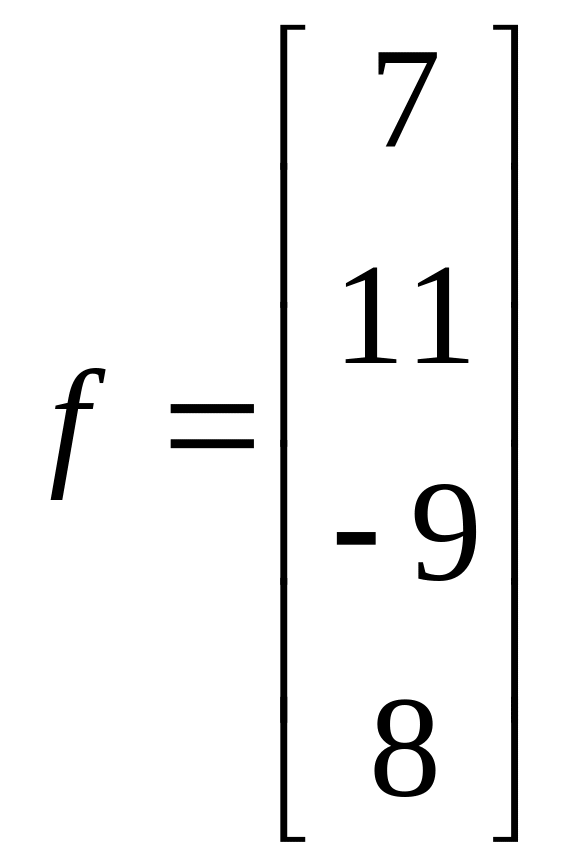Відшукати обернену матрицю до матриці методом Гаусcа з вибором головного елементу з точністю обчислень , а потім її уточнити із застосуванням алгоритму, наведеному в [9] (п.2.1 (стор. 39)) з точністю :

1.21. .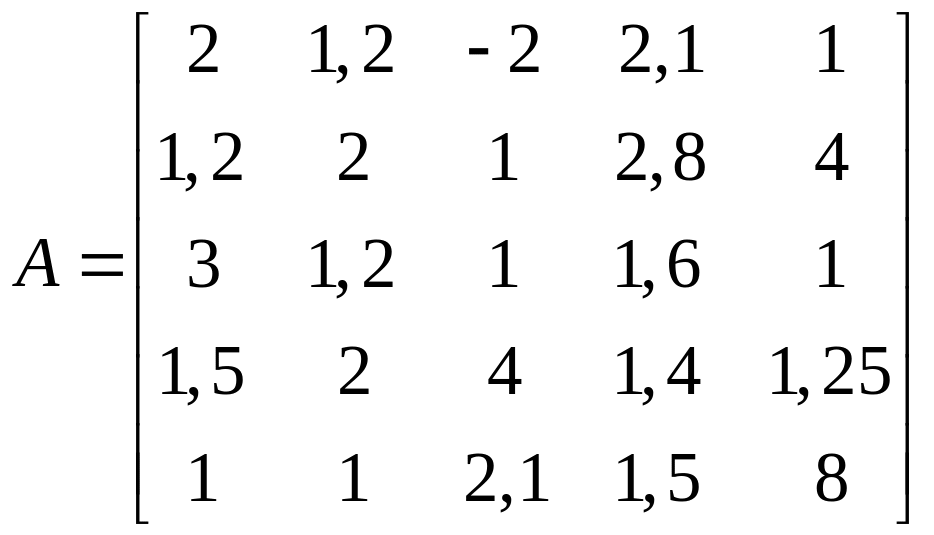

1.22. .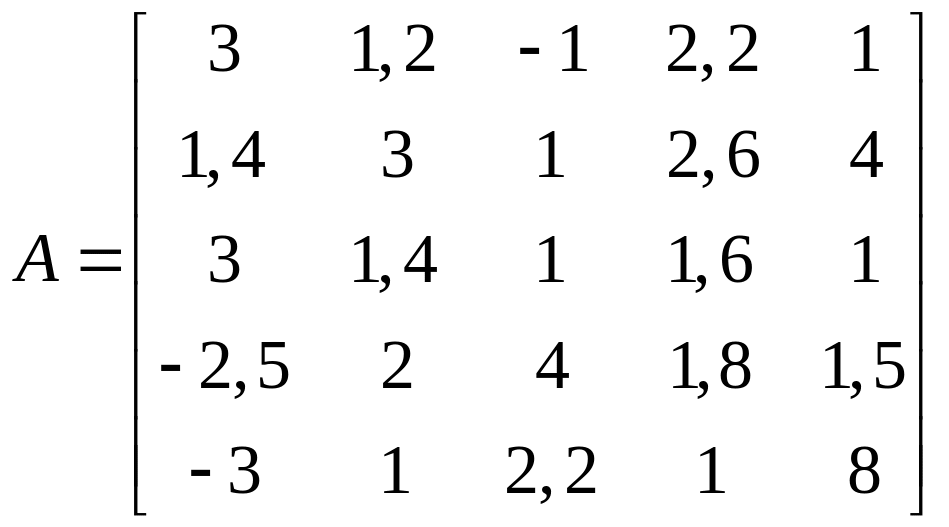

1.23. .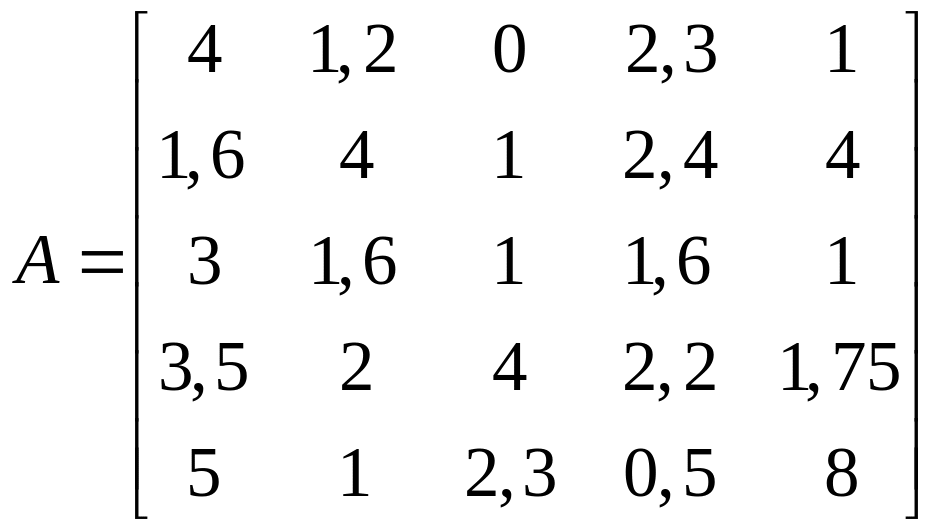

1.24. .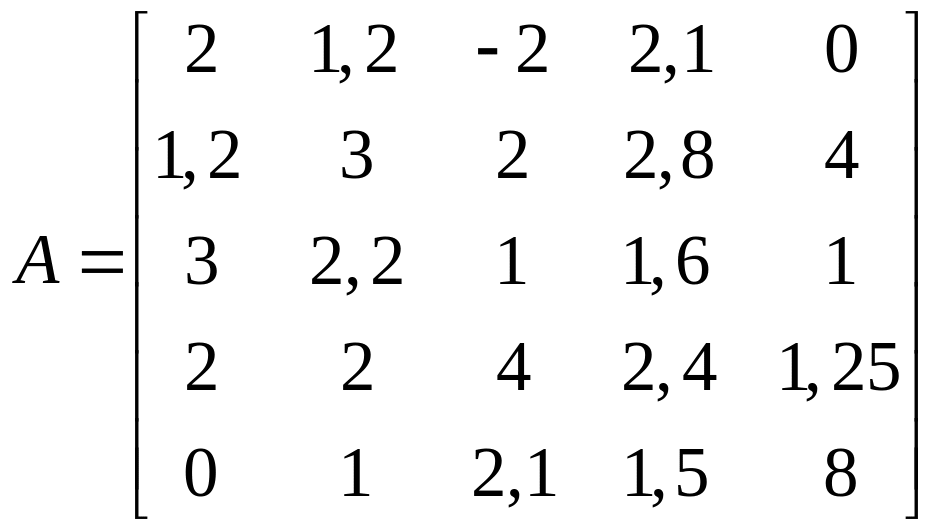

1.25. .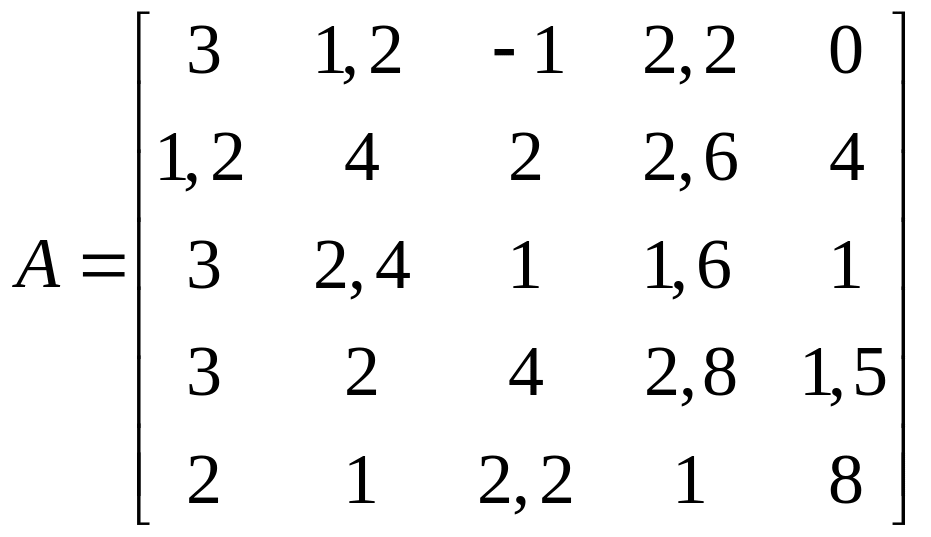

1.26. .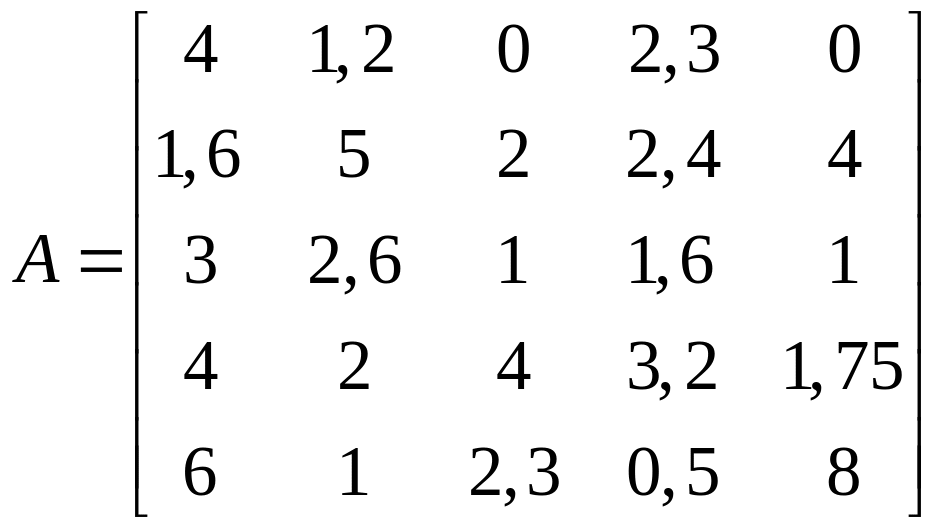

1.27. .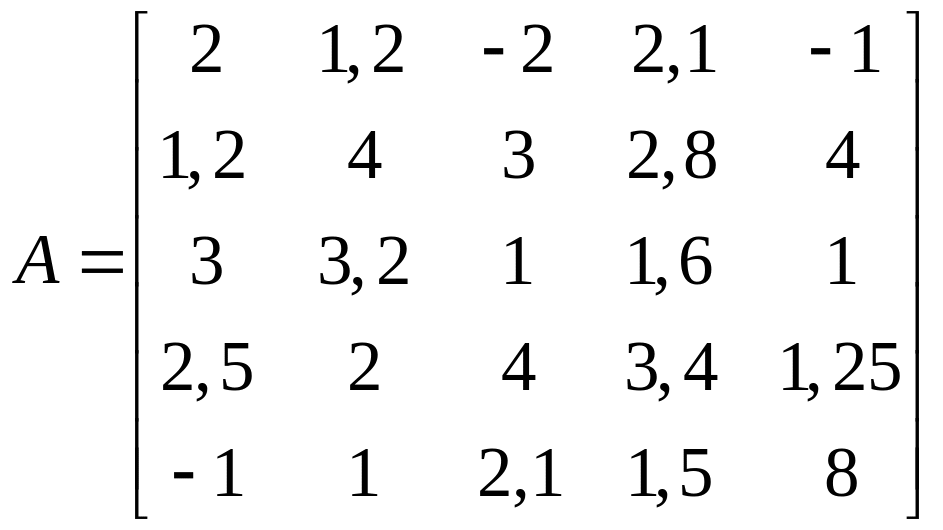

1.28. .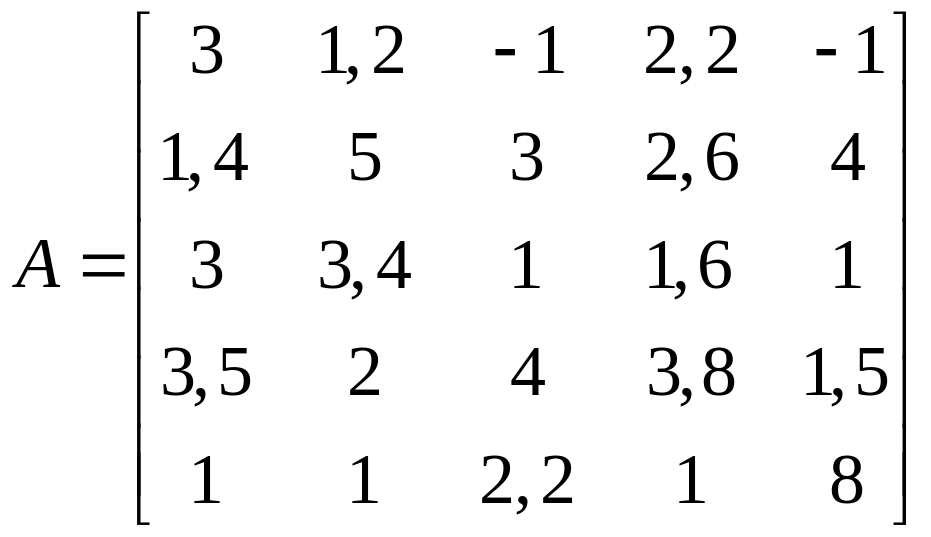

1.29. .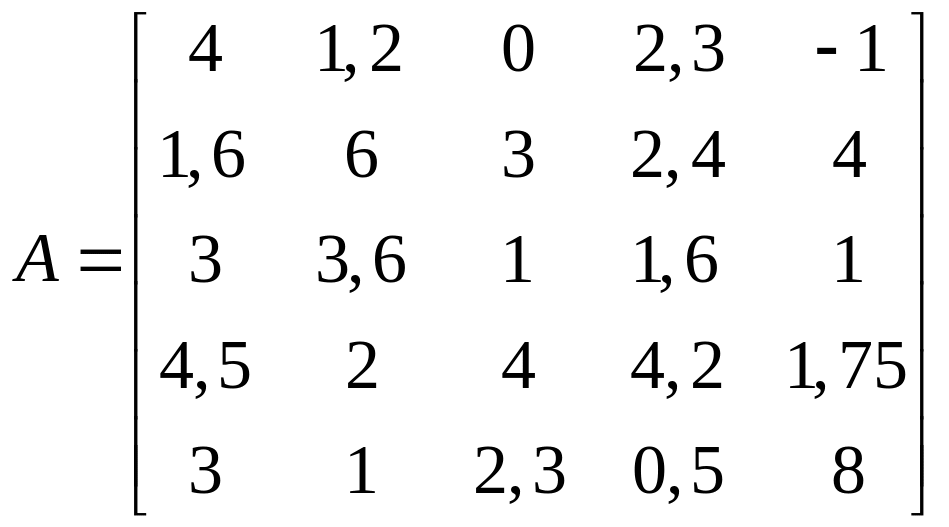

1.30. .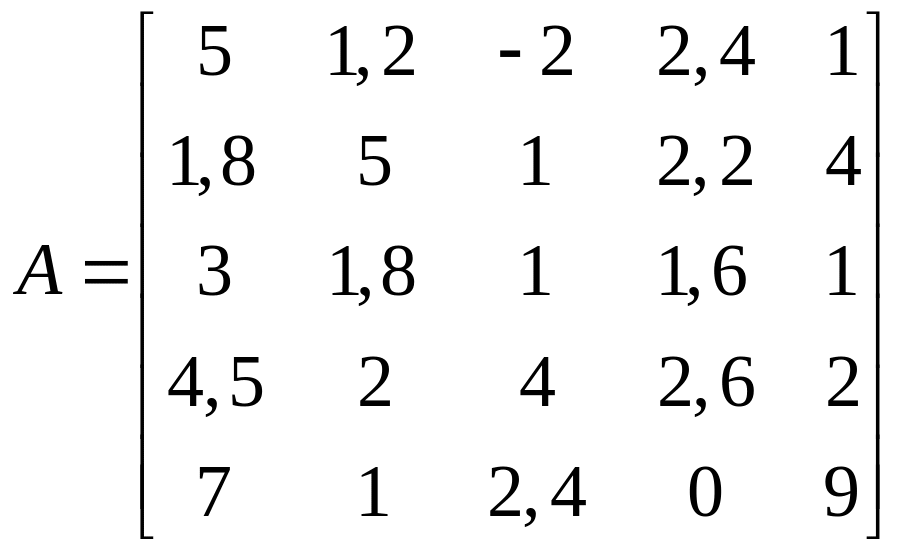

7.2 Завдання 2.

Визначити межі розташування дійсних коренів алгебраїчного рівняння , за допомогою теореми Штурма знайти їх кількість на одержаному відрізку, відділити їх (графічно або за допомогою алгоритму, наведеному в [9] п.4.3, стор. 67 - 71), та обчислити кожен, використовуючи один з ітераційних методів, наведеному в [9] (п.2.2, стор. 40 - 50) з точністю :

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

2.11.

2.12.

2.13.

2.14.

2.15.

2.16.

2.17.

2.18.

2.19.

2.20.

2.21.

2.22.

2.23.

2.24.

2.25.

2.26.

2.27.

2.28.

2.29.

2.30.

7.3 Завдання 3.

Розв’язати мішану задачу для рівняння

, ,

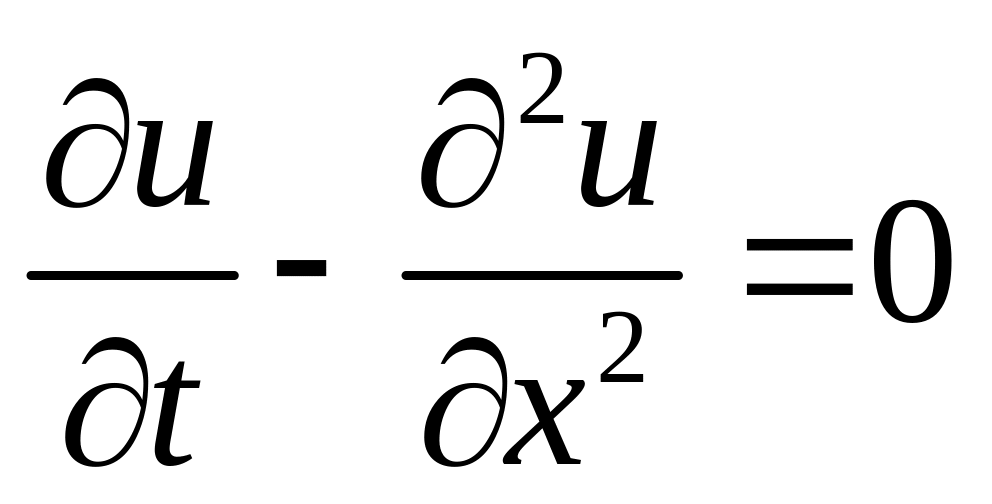з початковою умовою

та крайових умовах

,

Взяти ,

N	S(x)	p(t)	q(t)
3.1		0
3.2			1
3.3			1
3.4			0,5
3.5			0,8
3.6		1
3.7			0,4
3.8		0,2
3.9			0
3.10			1,5
3.11		0,8
3.12			0
3.13			0,6
3.14		0,2
3.15
3.16			0,5
3.17
3.18		0
3.19			0
3.20			1

Розв’язати сітковим методом задачу Коші для рівняння

, ,

з початковою умовою .

Взяти , , , забезпечити точність проміжних обчислень .

N	a	g(x)
3.21	5
3.22	3
3.23	2,5
3.24	4,5
3.25	2
3.26	3,5
3.27	4
3.28	5,5
3.29	1
3.30	1,5

Порівняти наближений розв’язок з точним.