2.2 Условный экстремум функций нескольких переменных при ограничениях в виде равенств и неравенств

Прикладные задачи, как правило, имеют такую особенность, что помимо ограничений типа равенств присутствуют ограничения типа неравенств вида

, (2.19)

где вектор . Например, при приобретении нового оборудования, предназначенного увеличить выпуск продукции, существуют ограничения на его стоимость. Таким образом, приходим к задаче получения максимальной прибыли при ограничении вида (2.19). Параметры конструкции, которыми мы можем в той или иной степени распоряжаться (угол поворота рулей, величина тяги двигателя и т.п.), всегда ограничены. И в этих случаях возникают задачи аналогичные по постановке задаче с закупаемым оборудованием.

Рассмотрим следующую задачу.

Минимизировать функцию

, (2.20)

где , при ограничениях в виде равенств

 , , (2.21)

и ограничениях в виде неравенств

 , . (2.22)

Дадим геометрическую интерпретацию поставленной задаче.

Каждое из ограничений (2.21), (2.22) в пространстве переменных выделяют соответственно области и (этот факт отражен в записях (2.21), (2.22)), т.е. в каждой точке области выполняются все ограничения (2.21), а в каждой точке области ограничения (2.22). Пересечение этих областей обозначим как область D. Таким образом, в каждой точке области D вычисляются как ограничения (2.21), так и ограничения (2.22).

Пример. Пусть при и должны быть такими, что

;

;

; (2.23)

.

Н а рис. 2.3 жирной линией показана допустимая область D, точки которой удовлетворяют ограничениям (2.23).

Используя понятие допустимой области, исходную задачу перефразируем так: среди точек допустимой области D найти такую точку, в которой целевая функция достигает минимума.

Ограничения типа неравенств превратим в ограничения типа равенств. Воспользуемся следующим приемом. Вместо (2.22) будем рассматривать равенства

, , (2.24)

где – подлежащие определению вещественные числа. Ограничения (2.22), (2.24) – эквивалентны. Действительно, какими бы не оказались числа , , а потому (2.22) и выполняются. Таким образом, получена задача (2.20), (2.21), (2.24), которая нами уже изучена (целевая функция с ограничениями в виде равенств). Формируем функцию

, (2.25)

где , и записываем необходимые условия экстремума функции по переменным , ; , ; , (всего таких переменных ):

, ;

, ; (2.26)

, ; (2.27)

,

Уравнений, как и неизвестных, .

Рассмотрим академический пример.

Пусть ,

.

Требуется найти такое значение , при котором целевая функция достигнет минимума.

Имея в виду приведенный выше алгоритм, последовательно запишем, что

,

где X – дополнительная неизвестная величина. Необходимые условия имеют вид:

;

;

.

Последнее уравнение полученной системы имеет два решения:

а) ; б) .

В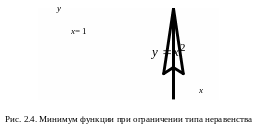 ариант а) в силу двух первых уравнений требует, чтобы , что не возможно. Вариант б) имеет решение: , т.е. (решение не удовлетворяет условию ).

Задача решена, рис. 2.4.