Вариант №11

1. Преобразования Галилея. Принцип относительности Галилея.

Преобразования Галилея – название преобразований в классической механике, согласно которым изменяются значения физических величин при переходе между различными инерционными системами отсчета. Преобразования Галилея позволяют описать физическое явление в инерциальной системе отсчета если известно как выглядит данное физическое явление в другой инерциальной системе отсчета. Если оси координат в двух системах отсчета имеют одинаковые направления, а одна система движется вдоль оси y второй системы с постоянной скоростью V, то преобразование имеют вид:

С оответственно меняются компоненты скорости:

принцип относительности галлилея

Другие величины, такие как ускорение, сила, масса при преобразованиях Галилея не меняются. Соответственно, не изменяется вид уравнений Ньютона. Говорят, что уравнение Ньютона инвариантны относительно преобразований Галилея.

пециальная теория относительности, созданная в 1905 г. А. Эйнштейном, стала результатом обобщения и синтеза классической механики Галелея-Ньютона и электродинамики Максвелла-Лоренца. «Она описывает законы всех физических процессов при скоростях движения, близких к скорости света, но без учета поля тяготения. При уменьшении скоростей движения она сводится к классической механике, которая, таким образом, оказывается ее частным случаем». Исходным пунктом этой теории стал принцип относительности. Классический принцип относительности был сформулирован Галилео Галилеем: «Если законы механики справедливы в одной системе координат, то они справедливы и в любой другой системе, движущейся прямолинейно и равномерно относительно первой.» Такие системы называются инерциальными, поскольку движение в них подчиняется закону инерции, гласящему: «Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, если только оно не вынуждено изменить его под влиянием движущихся сил." Галилей разъяснял это положение различными наглядными примерами. Представим путешественника в закрытой каюте спокойно плывущего корабля. он не замечает никаких признаков движения. Если в каюте летают мухи, они отнюдь не скапливаются у задней стенки, а спокойно летают по всему объему. Если подбросить мячик прямо вверх, он упадет прямо вниз, а не отстанет от корабля, не упадет ближе к корме. Из принципа относительности следует, что между покоем и движением — есть оно равномерно и прямолинейно — нет никакой принципиальной разницы. Разница только в точке зрения.

2.Виды поляризации. Вектор поляризации

 Атомная (электронная). Поляризации подвергаются заряды атома, в первую очередь деформируются электронные орбиты. Атомная поляризация может быть упругой, при которой энергия электрического поля практически не переходит в тепло. Если при атомной поляризации за счет взаимодействия атомов часть энергии электрического поля переходит в тепловую, поляризация называется релаксационной или тепловой.

 Ионная. При поляризации изменяется относительное расположение ионов в молекуле и (или) кристалле. Ионная поляризация может быть также упругой или релаксационной.

 Ориентационная (дипольная). При поляризации дипольные молекулы вещества стремятся ориентироваться по полю. Ориентируются также и диполи, образовавшиеся в результате ионной поляризации. При ориентационной поляризации часть энергии электрического поля переходит в тепло.

 Миграционная – под действием поля по веществу перемещаются отдельные заряды, возвращающиеся на прежнее место при исчезновении (снятии) поля. Длина пути этих зарядов может достигать 10^-3 м. У некоторых веществ (сегнетоэлектриков) при образовании кристалла может возникнуть спонтанная (самопроизвольная, без воздействия поля) поляризация, носящая ионный или дипольный характер. Микроскопические области со спонтанной поляризацией называются доменами.

Для количественной характеристики поляризации диэлектриков вводят понятие вектора поляризации как полного (суммарного) дипольного момента всех молекул в единице объема диэлектрика:

, - дипольный момент одной молекулы

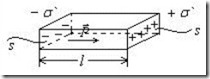
Суммирование производится по всем молекулам, находящимся в объеме V.Легко видеть, что нормальная составляющая вектора поляризации Р_n численно равна поверхностной плотности поляризационных зарядов на диэлектрике σ ^′ (рис.3.10):

Последняя формула дает не только величину, но и знак поляризационных зарядов. В тех точках поверхности диэлектрика, где угол θ между внешней нормалью и вектором острый, σ ^′ положительна, а в тех точках, где угол между внешней нормалью и тупой, σ ^′ отрицательна