3. Коэффициенты прямых и полных материальных затрат.

При исследовании модели межотраслевого баланса сначала нужно рассмотреть основные свойства матрицы коэффициентов прямых материальных затрат A.

Основные свойства матрицы коэффициентов прямых материальных затрат

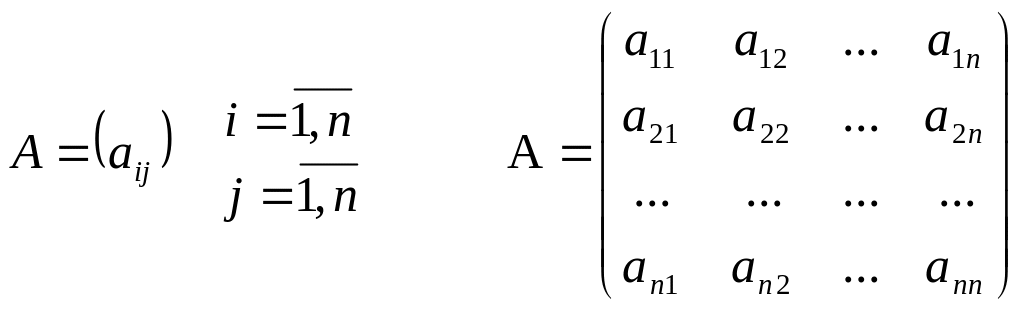
1. Коэффициенты прямых затрат по определению являются неотрицательными , поэтому матрица А в целом может быть названа неотрицательной: .

2. Диагональные элементы матрицы А меньше единицы , так как процесс воспроизводства нельзя было бы осуществлять, если бы для собственного воспроизводства в отрасли затрачивалось больше количество продукта, чем создавалось.

Система уравнений межотраслевого баланса является отражением реальных экономических процессов, в которых содержательный смысл могут иметь лишь неотрицательные значения валовых выпусков. Значит, вектор валовой продукции состоит из неотрицательных компонентов и называется неотрицательным, т.е. .

Экономическая система способна обеспечить положительный конечный выпуск по всем отраслям, если матрица коэффициентов прямых материальных затрат А является продуктивной.

Продуктивность матрицы А.

Неотрицательную матрицу А называют продуктивной, если существует такой неотрицательный вектор , что справедливо:

(13)

Это условие означает существование положительного вектора конечной продукции для модели межотраслевого баланса (7).

Существует несколько способов проверки продуктивности матрицы А.

Матрица коэффициентов прямых материальных затрат А продуктивна, если выполняется одно из условий:

1. Матрица неотрицательно обратима, т.е существует обратная матрица .

2. Матричный ряд сходится и его сумма равна обратной матрице .

3. Наибольшее по модулю собственное значение матрицы А меньше 1.

Собственные числа матрицы А – корни характеристического уравнения .

4. Все главные миноры матрицы , т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до n, положительны.

Наиболее простым, но только достаточным признаком продуктивности матрицы А является ограничение на величину ее нормы, т.е. на величину наибольшей из сумм элементов матрицы А в каждом столбце. Если норма матрицы А строго меньше единицы, то эта матрица продуктивна.

Но эти условия являются только достаточными, т.е. матрица А может быть продуктивной и в случае, когда ее норма больше единицы.

Пример № 1.

Проверить продуктивность матрицы . Найдем матрицу .

Найдем определитель матрицы

Находим элементы присоединенной матрицы ;

Сначала найдем транспонированную матрицу :

обозначим ее через D.

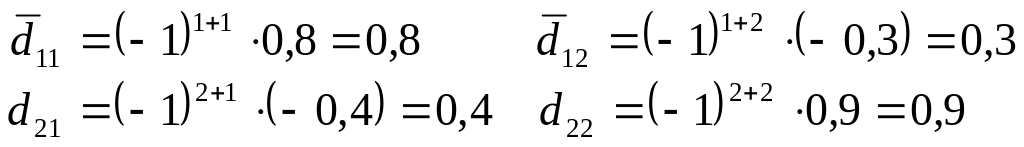
, значит, матрица А продуктивна.

Пример № 2.

Проверить продуктивность матрицы .

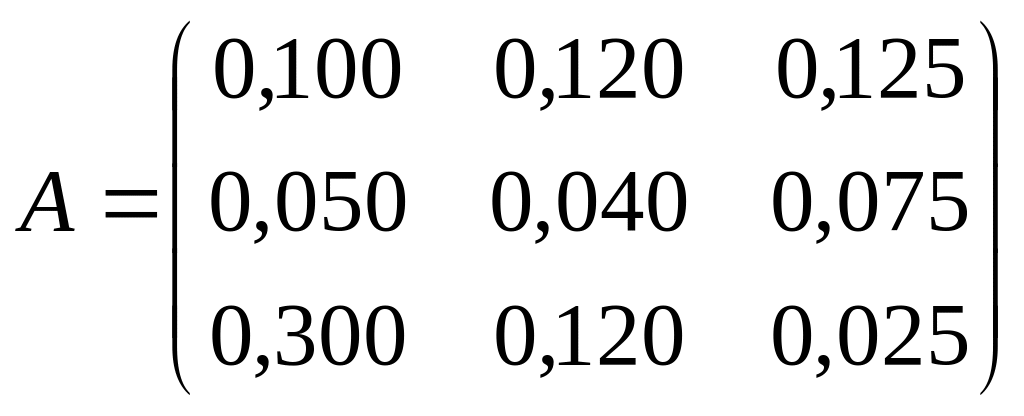Найдем главные миноры матрицы ;

.

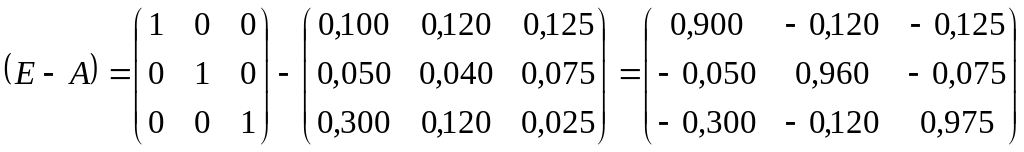Главный минор I-ого порядка: 0,900 > 0/

Главный минор II-ого порядка: > 0.

Главный минор III-его порядка: > 0.

Итак: все главные миноры матрицы положительны, значит матрица А является продуктивной.

Анализ матрицы коэффициентов полных материальных затрат.

Матрица - матрица коэффициентов полных материальных затрат .

Ранее было дано определение коэффициента b_ij полных материальных затрат, что b_ij показывает сколько нужно произвести продукции i-той отрасли, чтобы с учетом прямых и косвенных материальных затрат, получить единицу конечной продукции отрасли j.

Дадим другое определение коэффициента полных материальных затрат, исходя из того, что, кроме прямых затрат существуют косвенные затраты той или иной продукции при производстве продукции данной отрасли.

Например, при производстве автомобиля в виде прямых затрат расходуется уголь, стальной прокат, цветные металлы, электроэнергия и т.д. Но на производство стального проката также расходуется уголь. Это будут косвенные затраты I-го порядка при производстве автомобиля. При производстве стального проката расходуются цветные металлы, для производства которых также расходуется уголь. Но при производстве автомобиля это будут косвенные затраты II-го порядка и т.д.

В связи с этим имеет место следующее определение: коэффициентом полных материальных затрат (с_ij) называется сумма прямых затрат продукции i-той отрасли для производства единицы продукции j-той отрасли через все промежуточные продукты на всех предшествующих стадиях производства.

Обозначим коэффициент косвенных материальных затрат k-го порядка через , тогда имеет место равенство:

(14)

Если ввести в рассмотрение матрицу коэффициентов полных материальных затрат и матрицы коэффициентов материальных затрат различных порядков: , то можно записать формулу:

(15)

где А – матрица коэффициентов прямых материальных затрат;

А⁽¹⁾ – матрица коэффициентов косвенных материальных затрат I-го порядка;

А⁽²⁾ – матрица коэффициентов косвенных материальных затрат II-го порядка и т.д.;

А^(k) – матрица коэффициентов косвенных материальных затрат k-го порядка.

; и т.д. .

Итак: (16)

Если матрица коэффициентов прямых материальных затрат А является продуктивной, то из второго условия продуктивности следует, что существует матрица , которая является суммой сходящегося матричного ряда:

(17)

Тогда сопоставляя соотношения (16) и (17), можно сделать вывод о связи между двумя матрицами коэффициентов полных материальных затрат.

(18)

или

Экономический смысл различия между коэффициентами матриц В и С: в отличие от коэффициентов матрицы С, которые учитывают только затраты на производство продукции, коэффициенты матрицы В включают в себя кроме затрат также саму единицу конечной продукции, которая выходит за сферу производства.

Таким образом, если матрица А продуктивна, то для нахождения матрицы В можно использовать способы:

1. По формулам обращения матриц:

(19)

2. Приближенный способ по формулам разложения в матричный ряд:

(20)

В этом случае обычно ограничиваются косвенными затратами до некоторого порядка включительно.

Пример.

Дана матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

.

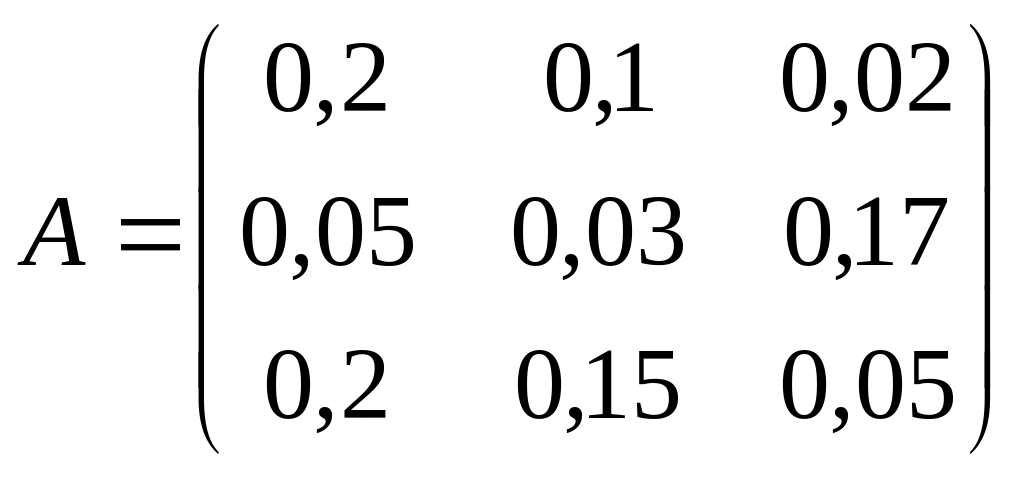
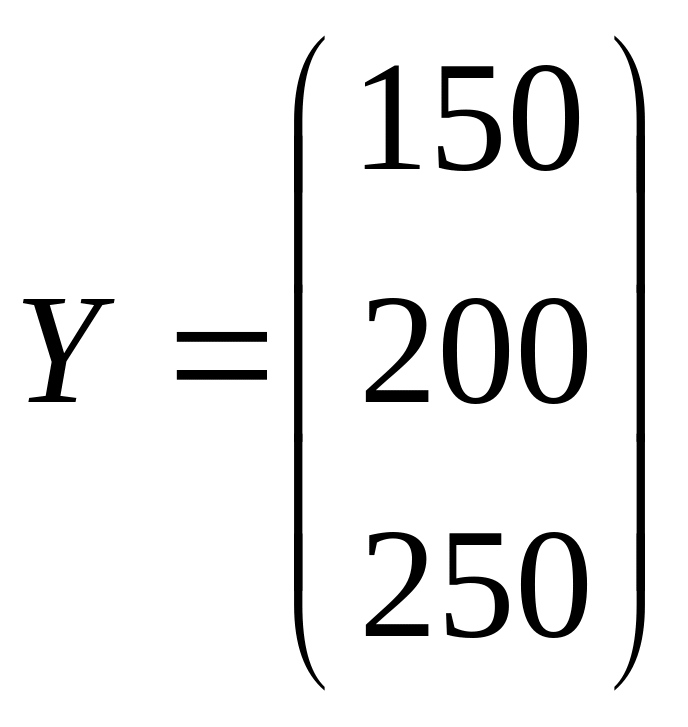Найти коэффициенты полных материальных затрат, вектор валовой продукции, заполнить схему межотраслевого баланса.

Решение:

1. Определитель матрицы : ;

2. Транспонируем матрицу : .

3. Находим алгебраические дополнения для элементов матрицы :

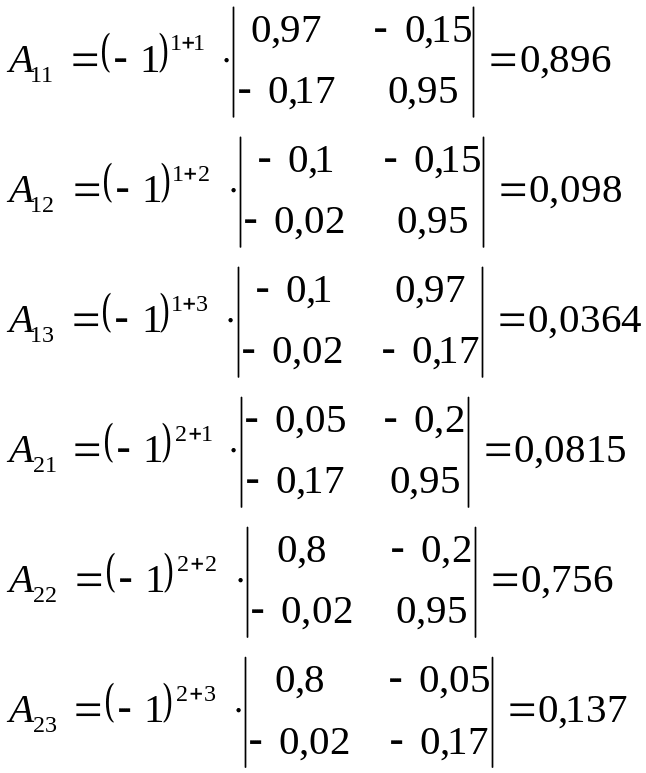
Присоединенная матрица:

Найдем вектор валовой продукции по формуле:

Для заполнения схемы межотраслевого баланса, необходимо найти:

Находим условно-чистую продукцию отраслей:

Межотраслевой баланс производства и распределения продукции:

Производящие отрасли	Потребляющие отрасли			Конечная продукция	Валовая продукция
	1	2	3
1 2 3	46,32 11,58 46,32	28,05 8,415 42,075	7,124 60,554 17,81	150 200 250	231,6 280,5 356,2
Условно-чистая продукция	127,38	201,96	270,712	600,0
Валовая продукция	231,6	280,5	356,2		868,3